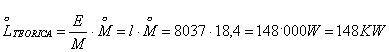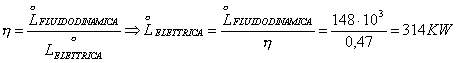INTRODUZIONE

Considerando lo studio di un fluido viscoso, in base alla velocità di scorrimento che esso ha all’interno di un tubo può trovarsi in:

-MOTO LAMINARE

-MOTO TURBOLENTO

-MOTO INSTABILE

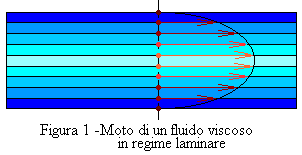
MOTO LAMINARE: Lo scorrimento del fluido avviene per strati paralleli alle pareti del tubo, con velocità che varia a causa della viscosità strato-strato, e strato-parete. La velocità pertanto aumenta mentre ci avviciniamo al centro del condotto (diminuisce la resistenza e di conseguenza aumenterà la velocità). Vedendo in sezione la situazione sopra descritta avremo (figura 1 e 2):

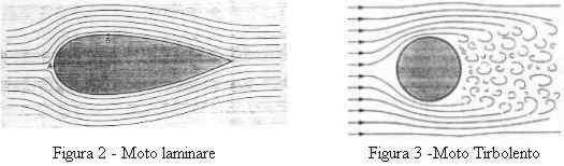
MOTO TURBOLENTO (figura 3): Lo scorrimento avviene in modo casuale non si riesce a schematizzare il movimento delle particelle in modo preciso. Tale regime è utile quando si progettano serpentine per il raffreddamento dell'acqua; se un fluido possiede un regime turbolento perde più in fretta calore rispetto al regime laminare. In questo modo si avranno serpentine più brevi ottenendo però lo stesso calo di temperatura.

MOTO INSTABILE: La situazione non è chiaramente determinata, il fluido nel suo scorrere passa in modo casuale dal moto turbolento al moto laminare in continuazione, non si conoscono le perdite di carico; questo regime, come si può chiaramente intuire è molto difficile da studiare, non che, da evitarsi assolutamente in ambito industriale, in quanto un’ipotetica turbina di un impianto potrebbe essere seriamente danneggiata (troppo sotto sforzo durante moto turbolento oppure girando quasi a vuoto in moto laminare)

Osborn Reynolds studiò in modo approfondito la dinamica dei fluidi, e durante i suoi esperimenti ne eseguì uno in particolare, tramite il quale riuscì a scoprire i fattori che governano il moto di un fluido all’interno di un condotto.

ESPERIMENTO DI REYNOLDS

L’esperimento, riproducibile anche in laboratorio senza l’utilizzo di strumenti troppo complicati, necessita di un serbatoio d’acqua in cui è innestato un tubo trasparente di scarico (trasparente per osservare il moto dell’acqua) e un iniettore all’ingresso di tale condotto tramite il quale far fuoriuscire una goccia d’inchiostro. (Vedi figura 4)

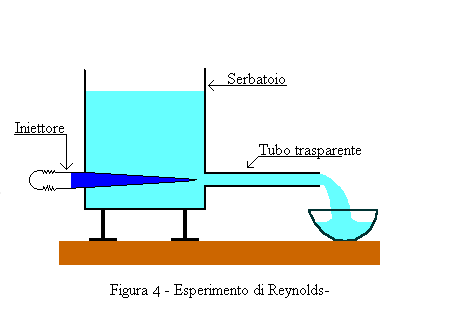
Variando la sezione del tubo, il tipo di fluido, oppure il pelo libero del liquido, avremo che la velocità di scorrimento del fluido varia; la goccia d’inchiostro servirà per visualizzare meglio il suo comportamento fluidodinamico. Quando la velocità di scorrimento sarà bassa (MOTO LAMINARE) avremo che la goccia persiste in un unico stato (figura 5), mentre quando la velocità sarà elevata, superiore a una certa quantità (MOTO TURBOLENTO), avremo che la goccia si mischia in modo quasi uniforme con il liquido (figura 6).

Reynolds durante l’esperimento trovò che le grandezze che influivano sul moto del fluido erano quattro: VELOCITA’ DI SCORRIMENTO w, SEZIONE DEL TUBO D, DENSITA’ DEL FLUIDO r, VISCOSITA’ DINAMICA DEL FLUIDO m, e confrontate a due a due, dedusse dallo studio dei relativi grafici che erano tutte legate fra loro secondo una precisa legge a cui diede il nome di NUMERO DI REYNOLDS

(1)

Lo studioso ripeté più volte la prova osservando in modo preciso il passaggio dal moto laminare a quello Turbolendo individuando un precisa velocità detta VELOCITA’ CRITICA.

Dall’esperimento ricavò in particolare che per un fluido qualsiasi se:

Re < 2100 avremo sicuramente moto laminare

Re > 4300 avremo sicuramente moto turbolento

2100 < Re < 4300 potremo avere sia moto laminare sia moto turbolento

2500 < Re < 3500 avremo moto instabile

Da una semplice analisi si nota che il numero di Reynolds è una quantità adimensionale; Il risultato raggiunto dallo studioso è pertanto sorprendente, in quanto tramite un semplice numero puro si può determinare la criticità del moto di un fluido.

Trattando con fluidi reali, avremo che la VISCOSITA' è una caratteristica fondamentale, e rappresenta la difficoltà che ha uno strato a scorrere su un altro strato. Un’equazione fondamentale della fluidodinamica è quella di Bernoulli:

(w2²-w1²)/2

g(z2-z1)

(p2-p1)/r+ R

-l

E. Cinetica

E. Potenziale

Fenomeni dissipativi

Lavoro specifico scambiato

Le grandezze in gioco sono:

w rappresentano le velocità medie d’ingresso e d’uscita.
g rappresenta l'accelerazione di gravità.
z sono le altezze dei due punti d’ingresso e uscita.
p sono le pressioni all'ingresso e all'uscita.
r rappresenta la densità del fluido
R rappresenta le perdite di carico
l è il lavoro specifico scambiato

Consideriamo tale equazione di bilancio energetico di un fluido lungo un tubo

(2)

Note tutte le grandezze in gioco, dovremo trovare le perdite di carico R sapendo che tale valore è funzione di un numero puro xchiamato coefficiente di perdite di carico:

(3)

Dove L è la lunghezza del condotto, D il diametro e w la velocità media di scorrimento.

Si noti che R ha dimensione [J/Kg], mentre x che è la nostra variabile è un numero puro.

Supponiamo ora di considerare un tubo avente stessa sezione e quota d’ingresso-uscita; dalla (2) si ricava

(4)

(N.B. Si riduce in questo modo dalle ipotesi fatte su sezione e quota: L=0, , )

che uguagliata con la (3) da:

(5)

Ora dalla legge (6) che lega la variazione di pressione Dp alla portata in volume (PARABOLA DI POISEUILLE)

(6)

sostituita nella (5) otteniamo

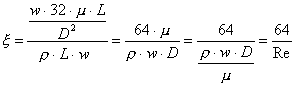(7)

Questa formula valida esclusivamente per il regime laminare è il raggiungimento di un risultato strepitoso, una relazione che lega un numero puro (variabile d’ingresso) con un altro numero puro, e che ci consente di affermare con assoluta certezza e precisione che due fluidi aventi caratteristiche diverse ( viscosità, sezione del tubo, velocità ) se hanno lo stesso numero di Reynolds Re allora avranno anche stesso x, ovvero avremo perdite di carico espresse tramite lo stesso x=x(Re) . Si osserva dalla (7) che mentre prima il coefficiente di perdite di carico dipendeva da tanti fattori quali la lunghezza, la sezione del tubo, la velocità, ora avremo che x è funzione di un solo parametro Re adimensionale.

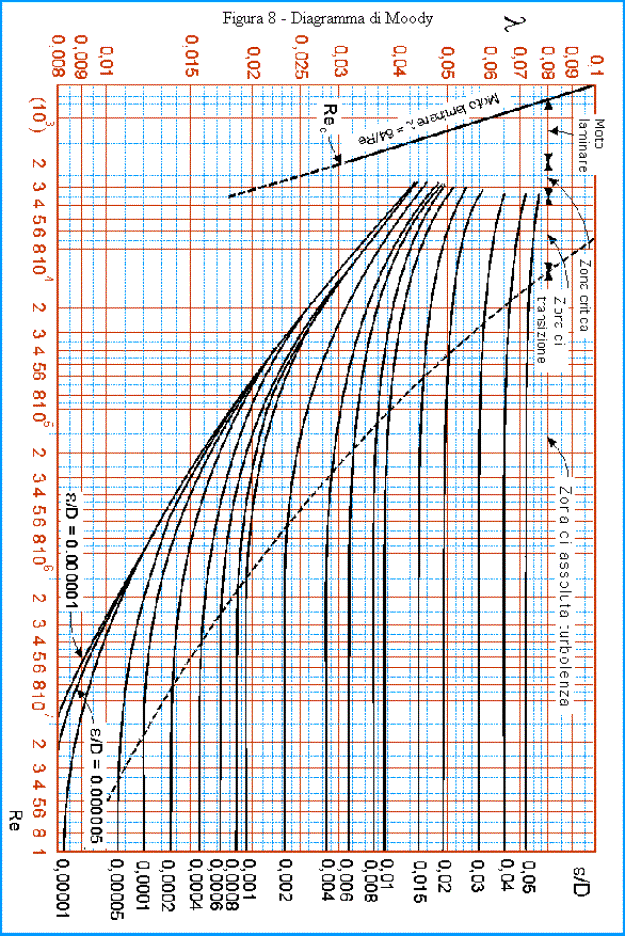
Esiste pertanto un diagramma, chiamato diagramma di Moody (figura 8), che esprime il coefficiente di perdite di carico in funzione del numero di Reynolds; notiamo da esso che vi saranno curve differenti all’aumentare della scabrezza relativa del tubo. Con più il tubo presenta rugosità interne significative con più saranno alte le perdite di carico. 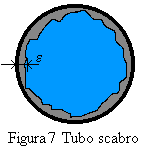Risulta allora chiaro perché in alcuni casi il coefficiente delle perdite relative è indicato come (8) funzione sia del numero di Reynolds, sia della scabrezza relativa (9) dove e è lo spessore medio della scabrezza e D è la dimensione caratteristica del condotto (Vedi figura 7). Abbiamo che la scabrezza può verificarsi non solo per un difetto di produzione ma essere dovuta a residui come calcare e ruggine.

ATTENZIONE: Abbiamo affermato che scabrezza influenza perdite di carico, ma non è vero che un tubo liscio non ha perdite di carico; è vero invece che nel primo caso avremo valori maggiori!

Un’analoga considerazione può essere fatta per il FATTORE DI FORMA (10) dove nel caso del tubo L = lunghezza del condotto e D = diametro; Otteniamo, considerando entrambi i fattori, che (11)

Durante i suoi studi, inoltre, Reynolds elaborò un’importante teoria a cui attribuì il nome di Teoria dei Modelli

TEORIA DEI MODELLI

L’idea di è che tutti i problemi fisici hanno una traccia risolutiva identica a patto che siano rispettati due criteri fondamentali:

1) Lavorare su equazioni fisiche dimensionalmente omogenee

2) Usare grandezze adimensionalizzate, ovvero ottenere equazioni contenenti solamente numeri puri.

Per adimensionalizzare occorre moltiplicare o dividere per opportune grandezze ogni termine dell’espressione in questione: sia un fluido che ha un profilo di velocità che aumenta di valore all’aumentare della distanza dalla parete del condotto. Indichiamo con v^* la velocità che assumerebbe per distanza infinita (velocità di riferimento) e con v la velocità relativa al problema da risolvere; avremo che la nostra velocità adimensionalizzata da usare sarà v_{adimensionale} = v / v^* . Da questo si nota che le grandezze che compaiono nell’equazioni saranno tutte comprese fra zero e uno (minimo e massimo).

Una volta soddisfatte queste due condizioni la soluzione del problema prevede sempre i medesimi passaggi matematici. Questa osservazione è molto importante perché ci consente di lavorare su modelli in scala così da trarre le stesse conclusioni che avremmo ottenuto lavorando sui modelli originali, risparmiando fatica e denaro. La teoria dei modelli elaborata da Reynolds trova applicazione in ogni ambito fisico, anche se lo studioso l’applicò solamente alla fluidodinamica e allo scambio del calore.

ESEMPIO

Studiare il flusso d’aria nei condotti di raffreddamento di un automobile da corsa avendo a disposizione un modello e una galleria del vento in scala 1:2.

Dati: -Lato condotto di raffreddamento del Prototipo

-Velocità Prototipo

-Viscosità cinematica dell’aria

Conoscendo la scala con cui stiamo lavorando, per ricreare una situazione fedele nella galleria del vento, ci verrebbe da affermare che le grandezze con cui studiare il problema siano tutte la metà di quelle originali:

Lato condotto di raffreddamento Modello

Velocità del Modello

In realtà si nota che tale idea è profondamente sbagliata, infatti, per il prototipo, tramite la (1) otteniamo , mentre per il modello avremo e quindi differente da quello reale. In questo modo studieremmo un altro caso e non quello che interessa a noi.

Allora per affrontare correttamente il problema bisogna ricavare il numero di Reynolds dai dati iniziali e usarlo per ottenere la velocità del modello . Con questo procedimento si ricava che per sistemi in scala 1:2 non bisogna dimezzare la velocità bensì raddoppiarla

Tale errore alle alte velocità può non essere significativo, (il diagramma di Moody presenta curve molto appiattite per moto molto turbolento); viceversa è molto evidente e rilevante alle basse velocità (si rischia di considerare laminare un moto che in realtà è turbolento, grosso errore).

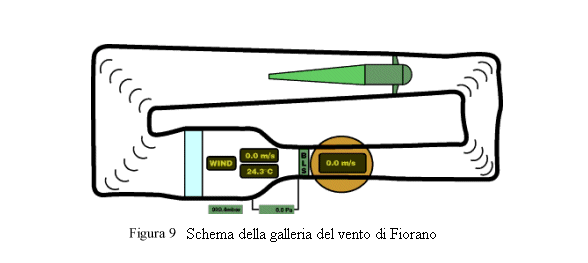
CURIOSITA’- Una galleria del vento è dotata di un sistema di acquisizione dati, e di sistemi di rilevazione delle forze. Altri sistemi consentono, inoltre, di rilevare con la massima precisione la velocità del vento, la sua direzione e la sua turbolenza. Nella galleria del vento di Fiorano (Figura9), il modello in scala può simulare ogni tipo d’assetto e di movimento (rollio, imbardata, sterzata e moti dinamici) per mezzo di un complesso meccanismo. Il modello è monitorato da oltre 300 sensori ed è possibile inoltre impiegare modelli in scala di vetture fino al 65% delle dimensioni reali, con la possibilità di provare anche vetture in scala 1:1.

In conclusione quando si risolve un problema di fluidodinamica solitamente si procede in tre passi:

Trovare numero di Reynolds Re
Ricavare coefficiente di perdite di carico x
Risolvere l’equazione di bilancio energetico ricavando le perdite di carico R

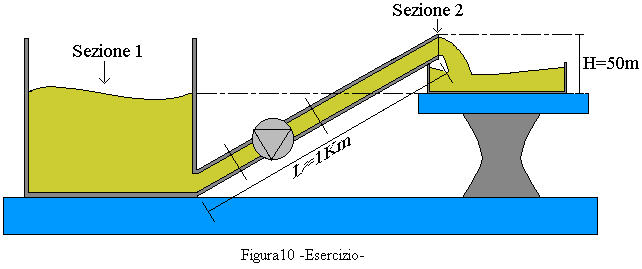
ESERCIZIO

Determinare la prevalenza e la potenza della pompa applicata al circuito riportato qui sotto (figura 10).

DATI: -Nel tubo, tondo e liscio, scorre olio da motore avente densità

e viscosità dinamica

-Diametro del tubo

-Lunghezza tubo

-Portata in volume condotto

N.B. Posizioniamo la pompa sotto il livello del fluido in modo che essa sia sempre sotto battuta ovvero il fluido arrivi ad essa in modo spontaneo; non occorrerà avere una pompa autoadescante

Scrivo l’equazione (2) del bilancio energetico,scegliendo in modo opportuno le sezioni 1 e 2 dell’impianto in modo da semplificarmi i calcoli. La scelta più intelligente sarà quella di considerare come sezione 1 il pelo libero del mascone, e come sezione due quella del tubo d’uscita del liquido; in questo modo avendo il serbatoio una sezione molto grande il livello del liquido si abbasserà ,molto lentamente in modo da poter considerare la velocità W₁ circa nulla.

Un’ulteriore semplificazione sarà considerare p₁ e p₂ uguali (in realtà la p₂ sarà leggermente maggiore).

Alla luce di queste considerazioni avremo:

(1. es)

Notiamo dalla formula che l’unica quantità a noi sconosciuta oltre alla prevalenza Dp, sarà il coefficiente di perdite di carico x(Re); Ricavo allora il numero di Reynolds e poi controllo sul diagramma di Moody la relativa x(Re).

(2. es)

Ricavo la velocità w₂

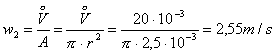(3. es)

che sostituita nella (2. es) da: Moto Laminare.

Trovandomi in tale regime ricavo x(Re) tramite la formula

(adimensionale)

Ora abbiamo tutto quello che ci serve per ricavare la prevalenza, perciò riprendendo la (1. es)

Calcolo i tre termini separatamente per valutare quanto ognuno di questi influenzi il risultato finale:

Si nota come il grosso del lavoro sia speso per far fronte alle perdite di carico; I primi due termini sono nettamente inferiori al terzo e quindi potrebbero essere trascurati. Procedo però con la somma

Da cui

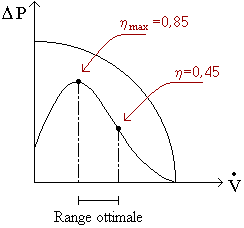
Determino la seconda specifica del problema, la potenza del motore.

Teoricamente la potenza sarebbe:

sapendo che

Per cui

Ma questa non è altro che la potenza fluidodinamica, a noi serve la potenza elettrica della pompa e quindi dobbiamo tener conto del suo rendimento

N.B. La curva di rendimento che è raffigurata nel grafico è diversa in base al modello della pompa usata; Quindi per risolvere il problema bisogna prendere il manuale delle specifiche della pompa, considerare il tratto di caratteristica ottimale e usare uno di questi valori per risolvere il problema. Nell’esercizio usiamo il valore minimo a scopo precauzionale, (se il rendimento è maggiore tanto meglio).

Essendo

Questo genere di problema è molto importante per ventilatori di condotti d’aerazione.