Gabriele Bozzetti – matr. 130403 – Lezione del 04/12/2001 - ora 16.30 – 18.30
ANALOGIA TRA FLUSSO TERMICO E FLUSSO ELETTRICO
Due sistemi si dicono analoghi quando sono retti da equazioni simili. Questo significa che l’equazione che descrive il comportamento di un sistema può essere trasformata nell’equazione dell’altro sistema cambiando semplicemente i simboli delle variabili.
Il
flusso di calore attraverso una resistenza termica è del tutto analogo al
flusso di corrente attraverso una resistenza elettrica.
Avendo
allora stabilito questa analogia fondamentale, si possono applicare ai problemi
di trasmissione del calore, alcuni concetti della teoria della corrente
continua.
Ricordiamo alcuni risultati ottenuti
dall’integrazione della legge di Fourier per geometrie piane e cilindriche
utili in seguito:
q lastra a facce piane e
parallele di spessore d, superficie S, e coefficiente di conduzione l:
![]()
q condotto cilindrico di
raggio interno R1, raggio esterno R2, lunghezza L, e
coefficiente di conduzione l:

q sfera cava di raggio interno
R1 ,
raggio esterno R2 e coefficiente di conduzione l:
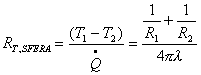
Calcolo di RT nel caso di
trasmissione convettiva del calore
Nel
caso di moti convettivi la dipendenza funzionale del flusso termico q (energia trasmessa per unità di tempo
per unità di superficie) dal gradiente di temperatura non è di tipo lineare,
come previsto dalla legge di Fourier, tuttavia è possibile ,ed estremamente
utile, ricondursi ad una forma semplice introducendo un fattore di
proporzionalità tra q e DT :
![]() non è una legge fisica,
serve solo per definire h
non è una legge fisica,
serve solo per definire h
dove
h, di dimensioni W/m2K, è
chiamato coefficiente di adduzione nonostante tale nome debba essere riservato,
secondo il Sistema Internazionale, unicamente a termini adimensionali.
La legislazione italiana (legge 10/91) prevede, per la progettazione di impianti di riscaldamento e di termoisolamento, l’utilizzo dei coefficienti h tabulati dalle norme UNI che stabiliscono anche le temperature ambientali di riferimento nelle diverse zone del paese.
h tiene conto degli effetti dovuti alla convezione e
all’irraggiamento,![]()
Ottengo
allora

Esercizio 1
Si
determini la potenza necessaria per mantenere un locale a 20°C quando la
temperatura esterna è 0°C ed il muro divisorio, costituito in mattoni dello spessore
di 25cm, ha una superficie di 10m2 (trascuro lo scambio termico
dovuto alle altre pareti).
S = 10m2
T1 = 20°C
T2 = 0°C
h1 = 8W/m2K ( per aria ferma )
h2 = 20W/m2K
l = 1W/m·K


Definisco
lo strato limite termico come il luogo dei punti a temperatura T* = 99% T1
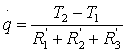 dove
dove![]() sono le resistenze termiche riferite all’unità di
superficie.
sono le resistenze termiche riferite all’unità di
superficie.
![]()
 moltiplicando per l’area
ottengo:
moltiplicando per l’area
ottengo: ![]()
Tenendo gli stessi dati dell’esercizio appena svolto ora considero una stanza ( di forma cubica per semplicità ) che scambia calore con l’esterno non più tramite una sola parete ma con ben 4 pareti + soffitto ( es. capannone ).
Atot
= 50 m2
![]()
Ora
tengo conto che nella stanza ci deve essere un ricambio d’aria , stabilito per
legge, di almeno 0.25 volumi all’ora ( 1 volume / ora nel caso di negozi e 2
volumi / ora per scuole, cinema …).
Volume
stanza = ![]()
![]() ( qui h sta per ora )
( qui h sta per ora )
La
massa d’aria che entra ( cioè che devo scaldare ) ogni ora è:
![]()
Posso
adesso calcolare la potenza necessaria a riscaldare l’aria:
![]() da confrontare con i 2350 W necessari per lo scambio termico dovuto
alle pareti.
da confrontare con i 2350 W necessari per lo scambio termico dovuto
alle pareti.
Esercizio 2
Si
determini la potenza necessaria per compensare la dispersione di un serbatoio
contenente acqua alla temperatura di 100°C se all’esterno vi sono 0°C. La
parete del contenitore è composta da una lastra in ferro, di spessore 5cm,
rivestita da un’alterna serie di pannelli, spessore 10cm, in cemento dalle
caratteristiche differenti.
lA = 60W/m·K (lastra in ferro)
lB1 = 1W/m·K (pannello in cemento 1)
lB2 = 0.1W/m·K (pannello in cemento 2)
TA =
100°C
TB =
0°C
hA = 200W/m2K è così elevato perché a contatto della
parete c’è l’acqua.
hB = 10W/m2K

Consideriamo
una porzione elementare di sezione complessiva 3 m2:
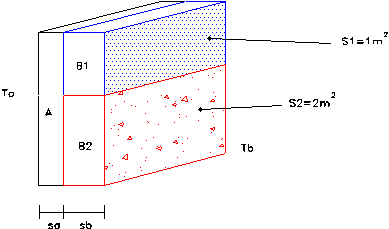
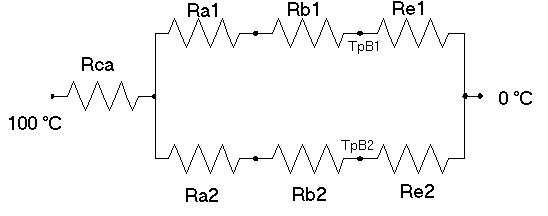
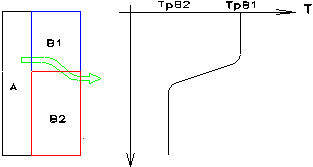
La
rete elettrica equivalente, nella quale le temperature di parete TpB1
e TpB2 sono giustamente considerate diverse, è la seguente:

Posso
anche schematizzare questo problema con un’altra rete elettrica, che stavolta
ammette che la lastra in ferro possa avere una temperatura diversa a seconda dell’isolante
( cemento ) che la divide dall’esterno.
Un’altra
schematizzazione può essere:
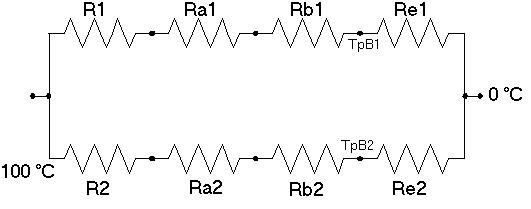
Nessuna
delle tre reti ha una preferenza ( nessuna rappresenta in modo esatto quello
che avviene ).
Del
resto sto rappresentando un sistema distribuito con un
modello a parametri concentrati.
Scelgo di risolvere l’ultima rete ( solo perché più facile ).
resistenza
di convezione acqua: ![]()
resistenza
di conduzione ferro A1: ![]()
resistenza
di conduzione cemento B1: ![]()
resistenza
di convezione aria: ![]()
resistenza
di convezione acqua : 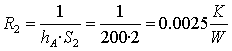
resistenza
di conduzione ferro A2: ![]()
resistenza
di conduzione cemento B2. 
resistenza
di convezione aria: 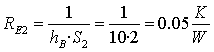
La
resistenza totale del primo ramo è:
![]()
La
resistenza totale del secondo ramo è:
![]()
![]()
![]()
![]()
Ora
posso calcolare le temperature di parete dei blocchi in cemento:
![]()
![]()
In
realtà la variazione di temperatura non è netta infatti, in corrispondenza dei
giunti strutturali B1/B2, si ha passaggio di calore che aumenta inevitabilmente
la potenza dispersa; per calcoli simili è quindi consigliabile adottare un
coefficiente di sicurezza che consideri questi fenomeni secondari.
Posso
anche calcolare la temperatura all’interno della parete, questo può essere
molto importante per evitare il fenomeno di condensa interstiziale.
Svolgendo
questi semplici esercizi ci siamo accorti di quanto sia importante ( per quanto
riguarda l’isolamento termico ) il valore di l: la fig. seguente mostra le
pareti di due case ; si nota molto bene che il flusso termico uscente dalla
casa di sinistra è maggiore rispetto a quello uscente dalla casa di destra.
Per
questo la scelta dei materiali edilizi non viene fatta solo sulla base
dell’estetica o della robustezza ma si tiene conto anche della conducibilità
dei materiali ( mettendo dei pannelli isolanti ).

Come si trovano i valori di l ?
Innanzitutto
occorre un provino del materiale di cui vogliamo misurare il coefficiente di conducibilità
( per legge deve essere di base quadrata 500 X 500 mm e alto s).
![]()
Ci sono due metodi principali per valutare l:
METODO DELLA LASTRA PIANA DOPPIA
Questo
metodo è molto costoso: servono due provini e la misura può durare più giorni.
Questo
metodo è molto preciso, viene usato anche per tarare altri strumenti di misura.
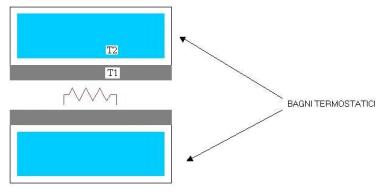
Genero
calore tra i due provini ( in grigio nella fig. ) per effetto Joule tramite una
resistenza: in questo modo conosco esattamente il calore che fornisco.
Solitamente
è presente un anello di guardia attorno al dispositivo per ridurre gli effetti
di bordo, sono così sicuro che il flusso di calore è normale alla lastra.
![]() dove con s indico lo
spessore del provino.
dove con s indico lo
spessore del provino.
In questa equazione l’unica incognita è l e quindi posso appunto ricavare il coefficiente di conducibilità termica.
TERMOFLUSSIMETRO
Questo
metodo è più veloce del precedente ed inoltre occorre un solo provino ( nero in
fig. ).
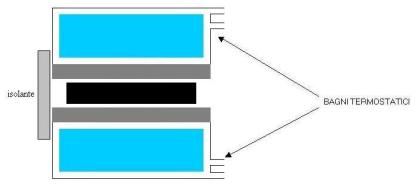
Il termoflussimetro
( grigio in fig. ) è un tappetino di gomma ( di cui conosco l ) con montata una termocoppia differenziale.
Le f.e.m. della termocoppia sono in serie, quindi si sommano; percui la termocoppia risulta essere molto sensibile.
DV misurato è proporzionale a DT sopra e sotto il
termoflussimetro.
![]() DT lo conosco perché conosco DV
DT lo conosco perché conosco DV
R la conosco, il suo
valore è scritto sul termoflussimetro
Allora
posso ricavare Q.
Da ![]() ricavo l
ricavo l
Un
difetto del termoflussimetro da tenere in considerazione è che questo strumento
ha bisogno di essere tarato molto spesso, in quanto le proprietà del
materassino di gomma possono variare.