Dispositivi di raffreddamento
Uno dei problemi spesso incontrati dal progettista elettronico è la necessità si smaltire il calore generato delle apparecchiature al fine di garantirne il miglior funzionamento. Una delle soluzioni spesso utilizzate per assicurare la dissipazione del calore è la convezione naturale o forzata con l’aria, ma questo spesso non è sufficiente, infatti la scarsa conducibilità termica e viscosità dell’aria (λ aria secca = 0.026 W/mK, η aria secca = 1.8 ![]() 10-5 Ns/m2), fanno si che i coefficienti di convezione (h) lato-aria non superino i 30-40 W/m2K, di conseguenza il fattore che acquista la maggiore importanza in questo tipo di processo è la superficie a contatto con l’aria: Rendere tale superficie idonea allo scambio termico migliora nettamente le prestazioni del processo.
10-5 Ns/m2), fanno si che i coefficienti di convezione (h) lato-aria non superino i 30-40 W/m2K, di conseguenza il fattore che acquista la maggiore importanza in questo tipo di processo è la superficie a contatto con l’aria: Rendere tale superficie idonea allo scambio termico migliora nettamente le prestazioni del processo.
Accrescere,quindi , la quantità d’aria soffiata sulla superficie interessata apporta qualche beneficio ma non da gli effetti sperati, infatti con la sola "forzatura" dell’aria i coefficienti di convezione h non superano i 50 W/m2K. Se la potenza da dissipare è maggiore, l’unica cosa da fare, è aumentare la superficie di scambio per migliorarne il rendimento.
 Fig. 1 - Pentium pro
Fig. 1 - Pentium pro
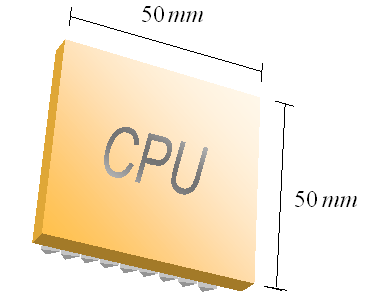
Supponiamo di avere un componente elettronico, ad esempio la CPU di un computer, un vecchio Intel Pentium Pro (per informazioni cliccare sulla foto), e supponiamo che la superficie di scambio S sia quadrata e di aria pari a 2500 mm2 (ipotiziamo un lato di 50 mm).
Il Pentium Pro introdotto da Intel nel 1995, è considerato uno dei migliori processori del periodo ma, pur essendo costruito con invidiabili tecnologie, ha una potenza da dissipare molto alta.
 Fig. 2 - Calore dissipato dalla Cpu
Fig. 2 - Calore dissipato dalla Cpu
Supponiamo che tale potenza sia ![]() = 50 W , e che il coefficiente di convezione, essendo estremamente ottimisti, sia h = 20 W/m2K, vogliamo determinare la temperatura d’esercizio in condizione di sola convezione naturale. La dissipazione del calore avviene solo dalla facciata esposta verso l’esterno (l’altra, naturalmente, è a contatto con la scheda madre, lo scambio termico con essa viene trascurato), mentre il calore scambiato con l’aria tramite la superficie laterale della CPU è trascurabile, essendo trascurabile la superficie stessa.
= 50 W , e che il coefficiente di convezione, essendo estremamente ottimisti, sia h = 20 W/m2K, vogliamo determinare la temperatura d’esercizio in condizione di sola convezione naturale. La dissipazione del calore avviene solo dalla facciata esposta verso l’esterno (l’altra, naturalmente, è a contatto con la scheda madre, lo scambio termico con essa viene trascurato), mentre il calore scambiato con l’aria tramite la superficie laterale della CPU è trascurabile, essendo trascurabile la superficie stessa.
I dati in nostro possesso sono:
vogliamo determinare, quindi, la temperatura Tp della Cpu.
La potenza da dissipare è :
![]() ( 1 )
( 1 )
S è la superficie della CPU che è uguale al quadrato del lato:
![]()
quindi unendo le precedenti e ed isolando Tp otteniamo:
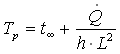
passando dai simboli hai numeri:
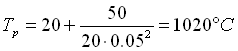 ( 4 )
( 4 )
Evidentemente la CPU ad una tale temperatura non può fare altro che bruciare in pochi secondi, infatti il Pentium Pro era termicamente delicatissimo, bastavano pochi attimi di malfunzionamento del sistema di raffreddamento a danneggiare irreparabilmente la CPU.
Il metodo più semplice a cui si può far ricorso per migliorare l’efficienza di dissipazione da parte della superficie di scambio termico è, come già accennato, quello di passare da una convezione naturale ad una convezione forzata.
Per fare ciò ci serviamo di una ventola posta sopra la CPU che soffia aria a temperatura ambiente sulla superficie di scambio.
 Fig. 4 - CPU munita di ventola
Fig. 4 - CPU munita di ventola
Supponiamo che, con questa tecnica, il coefficiente di convezione h diventi pari a 50 W/m2K allora la ( 4 ) diventa :
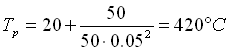
Come dimostrato la temperatura Tp della CPU si è abbassata, ma 420°C sono ancora troppi per un componente elettronico che dovrebbe avere una temperatura d’esercizio pari a circa 100-120°C, tale tecnica non è sufficiente.
Proviamo allora ad aumentare la superficie di scambio applicando sulla CPU una piastra in alluminio (λ alluminio = 220 W/mK a 20°C) di lato L pari a 100 mm, allora la ( 5 ) diventa:
![]()
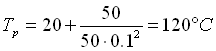 ( 6 )
( 6 )
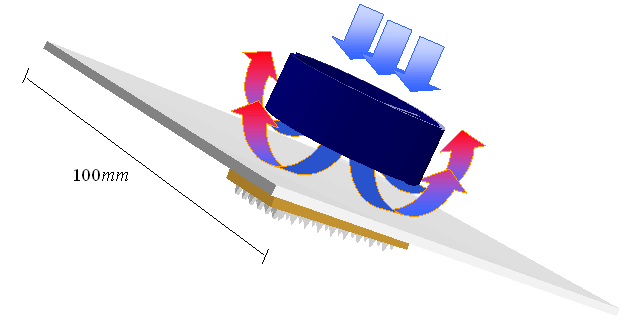
Fig. 5 - Piastra in alluminio posta a contatto della CPU
Tale temperatura è da ritenersi accettabile, ma, anche in questo caso, insorgono alcuni problemi: dapprima vi è un incertezza nel calcolo, infatti la non è detto che la temperatura della piastra in alluminio sia uguale dappertutto (il calore defluisce dal core verso l’esterno più freddo, dando luogo ad un minor scambio termico); d’altra parte vi è un problema di ingombro (una superficie di 0.01 m2 è difficilmente collocabile all’interno di luogo, spesso ristretto, come può essere il case di un computer).
Superfici alettate
La soluzione più comunemente usata, in linea di principio identica all’ ultima tecnica analizzata, è quella di aumentare la superficie di scambio non tramite una piastra unica, ma tramite una superficie alettata, ossia un’area fornita di alette disposte parallelamente tra loro. Tale espediente è naturalmente semplificato, infatti ci sono molte forme anche complesse atte a migliorare l’aerodinamica e quindi l’efficienza dei dissipatori ad alette (nella foto dissipatore in alluminio della Thermalright, cliccare sulla foto per informazioni in italiano, sul nome della ditta per la home page della stessa).
 Fig. 6 - Dissipatore della Thermalright
Fig. 6 - Dissipatore della Thermalright
Comunque la semplificazione fatta non è così lontana dalla realtà, ad esempio i dissipatori studiati per il Pentium Pro avevano forme molto più semplici e vicine all’esempio fatto.
 Fig. 7 - Dissipatore della Coolerguys per Pentium pro
Fig. 7 - Dissipatore della Coolerguys per Pentium pro
Con la superficie alettata si cerca di ottenere circa la stessa area che avevamo dimostrato sufficiente, col sistema della piastra in alluminio, a raffreddare il core.
Principio di Efficienza dell’alettatura
Supponiamo di avere una CPU sormontata da una superficie alettata e quindi da una ventola (vedi illustrazione), in questo modo abbiamo aumentato la superficie di scambio, ma ritroviamo anche il problema gia riscontrato della differenza di temperatura tra le varie parti del dissipatore.
 Fig. 8 - Esempio di dissipatore
Fig. 8 - Esempio di dissipatore
Possiamo dire infatti che la base delle alette, ad immediato contatto col processore, hanno , a parte una piccola resistenza di contatto, una temperatura molto vicina a Tp, viceversa, lungo il lato delle alette, la temperatura decresce verso la temperatura T∞ dell’ambiente (vedi illustrazione, in questo caso chiamiamo L la lunghezza dell’aletta).
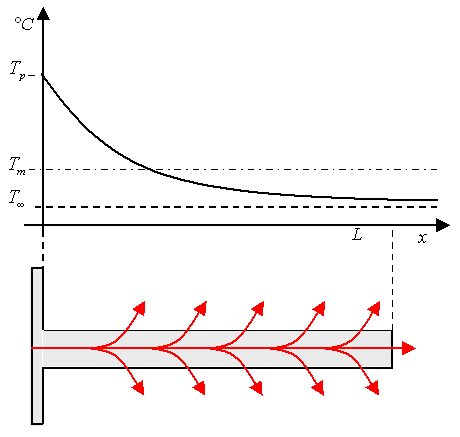
Fig. 9 - Temperature dell’aletta in funzione della distanza dalla CPU
Chiaramente la riduzione della temperatura al crescere della distanza dalla CPU ne riduce lo scambio termico. Possiamo comunque ovviare a tale problema considerando lo scambio termico come se avvenisse ad una temperatura media, Tm, costante e minore di Tp o come se avessimo un coefficiente di scambio termico più basso.
Sostanzialmente non si può pensare ad un aumento dello scambio termico direttamente proporzionale all’aumento della superficie, in quanto ciò sarebbe possibile solo se il dispositivo di raffreddamento fosse un dispositivo ideale, con conducibilità termica infinita e quindi con una temperatura costantemente uguale alla temperatura della CPU in tutta la sua struttura. Vogliamo quindi quantificare il rendimento di un’alettatura reale rispetto al caso ideale, ossia mettere a confronto lo scambio termico effettuato da essa con quello di un’alettatura tutta a temperatura Tp.
Il concetto appena espresso prende il nome di efficienza. Tale concetto può essere esteso alla sola aletta o all’intera superficie alettata. Tali valori sono solitamente numericamente diversi.
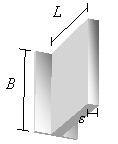
Se consideriamo una sola aletta, dimensionando come in figura, la sua superficie vale:
![]()
allora l’efficienza dell’aletta è:

ossia è il rapporto tra la potenza effettivamente scambiata dall’aletta e la potenza che l’aletta scambierebbe se fosse tutta a temperatura Tp (ovviamente tale numero è sempre minore di uno). Considerando invece la superficie totale del dissipatore e la potenza da esso scambiata, si definisce l’efficienza dell’intera superficie alettata εsup.alettata .
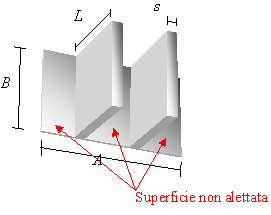
La superficie totale Stot è la somma della superficie non alettata Snon alettata e della superficie delle alette Salette:
dove Snon alettata è :
ed Salette è :
![]() ( 11 )
( 11 )
con Nalette uguale al numero di alette.
Quindi chiamando ![]() la potenza dissipata dell’intera superficie alettata la sua efficienza εsup. alettata è:
la potenza dissipata dell’intera superficie alettata la sua efficienza εsup. alettata è:
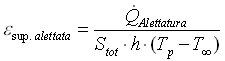
Funzionamento
Determiniamo ora come varia la temperatura lungo il profilo di un’aletta. Abbiamo osservato che essa non è costante ma decresce con la componente x parallela alla lunghezza dell’aletta (vedi Fig. 9). Per determinare la legge che lega la temperatura ad x si usa un ragionamento gia osservato nello studio degli scambiatori di calore, ovvero si prende un elemento infinitesimo dx dell’aletta, e si evidenziamo i flussi di calore che entrano ed escono da esso.
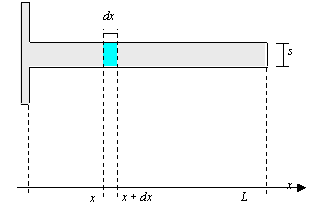
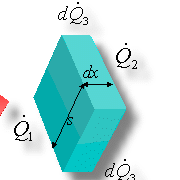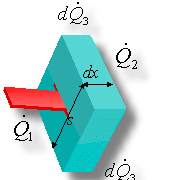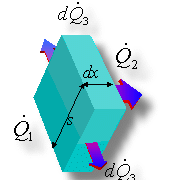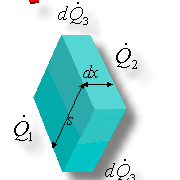 Fig. 12 - Rappresentazione di un elemento infinitesimo dell’aletta
Fig. 12 - Rappresentazione di un elemento infinitesimo dell’aletta
Chiamiamo ![]() la potenza scambiata per pura conduzione attraverso la sezione dell’aletta contrassegnata con l’ascissa x,
la potenza scambiata per pura conduzione attraverso la sezione dell’aletta contrassegnata con l’ascissa x, ![]() la potenza scambiata anch’essa per conduzione attraverso la sezione contrassegnata con l’ascissa x+dx e
la potenza scambiata anch’essa per conduzione attraverso la sezione contrassegnata con l’ascissa x+dx e ![]() quella scambiata per convezione con l’aria tramite la porzione di aletta delimitata dalle coordinate x e x + dx. Naturalmente la potenza scambiata
quella scambiata per convezione con l’aria tramite la porzione di aletta delimitata dalle coordinate x e x + dx. Naturalmente la potenza scambiata ![]() è dovuta ad un flusso di calore che entra nell’elemento, mentre
è dovuta ad un flusso di calore che entra nell’elemento, mentre ![]() e
e ![]() sono dovute ad un flusso di calore uscente, per conduzione e convezione, dall’elemento. Per il bilancio dell’energia in regime stazionario, procediamo eguagliando la potenza entrante con quella uscente ed otteniamo:
sono dovute ad un flusso di calore uscente, per conduzione e convezione, dall’elemento. Per il bilancio dell’energia in regime stazionario, procediamo eguagliando la potenza entrante con quella uscente ed otteniamo:
![]() ( 13 )
( 13 )
Come vediamo mentre le potenze scambiate per conduzione sono finite, la loro differenza è infinitesima, infatti ![]() è proporzionale alla superficie di scambio che a sua volta è proporzionale a dx.
è proporzionale alla superficie di scambio che a sua volta è proporzionale a dx.
Calcoliamo adesso le potenze scambiate attraverso il metallo per sola conduzione, possiamo utilizzare la legge di Fourier per calcolare la potenza di conduzione q(x):
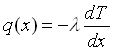 ( 14 )
( 14 )
dove λ è la conducibilità termica del materiale di cui è fatta l’aletta mentre T è il valore della temperatura che, nell’ipotesti di alette di piccolo spessore s ,varia solo con l’ascissa x.
Quindi avremo che il calore entrante nell’elemento alla coordinata x sarà:
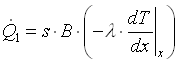
Utilizzando lo sviluppo di Taylor nel punto x+dx si avrà:
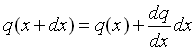 ( 16 )
( 16 )
e quindi il la potenza scambiata attraverso la sezione passante per x + dx sarà:
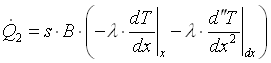
Unendo la 13, la 15 e la 17 otteniamo che:
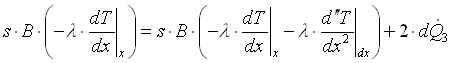
Sviluppando e semplificando si ottiene facilmente:
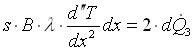
La potenza ![]() scambiata per pura convezione utilizzando la 1 sarà:
scambiata per pura convezione utilizzando la 1 sarà:
![]()
ma
![]()
e sostituendo la 21 nella 20 ed il risultato nella 19 otteniamo:
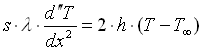
Per comodità poniamo![]() e notando che se sostituisco
e notando che se sostituisco![]() al posto di T nella derivata seconda non cambia nulla, visto che sommo solo una costante che si elimina derivando, ottengo:
al posto di T nella derivata seconda non cambia nulla, visto che sommo solo una costante che si elimina derivando, ottengo:
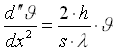
poniamo ora 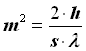 si ottiene:
si ottiene:
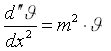 ( 24 )
( 24 )
m prende il nome di costante di estinzione dell’onda.
Tale è l’equazione di D’Alembert (gia vista in acustica), le cui soluzioni sono:
![]() ( 25 )
( 25 )
Tale condizione, diversamente da quanto accadeva in acustica, dove m2 era negativo, è sempre verificata (ha soluzioni reali). Secondo le equazioni di Eulero ![]() rappresenta un equazione d’onda smorzata. Si possono quindi determinare A e B usando le condizioni al contorno.
rappresenta un equazione d’onda smorzata. Si possono quindi determinare A e B usando le condizioni al contorno.
Per la condizione iniziale non vi sono problemi, bisogna solo tener conto di una piccola resistenza di contatto Rc, dovuta al fatto che comunemente l’aletta non fa parte del componente ma è semplicemente messa a contatto con esso.
Per la condizione finale bisogna fare una precisazione: per x = L lo scambio termico avviene per convezione, ![]() non è più scambiata per conduzione e quindi il calcolo si complica. Possiamo ovviare a tale problema trascurando la potenza scambiata per convezione in x = L, imponendo cioè
non è più scambiata per conduzione e quindi il calcolo si complica. Possiamo ovviare a tale problema trascurando la potenza scambiata per convezione in x = L, imponendo cioè ![]() , ma ciò se può andare approssimativamente bene per alette "snelle", ossia con s << L , non altrettanto con quelle "tozze", cioè dove L ed s sono confrontabili.
, ma ciò se può andare approssimativamente bene per alette "snelle", ossia con s << L , non altrettanto con quelle "tozze", cioè dove L ed s sono confrontabili.
Una buona soluzione è aumentare il valore numerico di L di s/2, come se proiettassimo l’area della testa dell’aletta metà sulla superficie superiore e metà su quella inferiore, chiameremo lunghezza corretta Lc la somma:
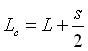
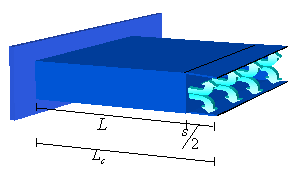 Fig. 13 - Come ottenere Lc
Fig. 13 - Come ottenere Lc
Con questo semplice trucco, maggiorando la lunghezza dell’aletta con a metà del suo spessore, possiamo tranquillamente trascurare la potenza scambiata sull’estremità di essa ritrovando un’equazione risolutiva molto più semplice.
Le condizioni di contorno, dunque,diventano:
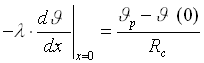
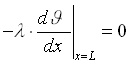
dove![]() e
e ![]()
Risolvendo otteniamo:
![]()
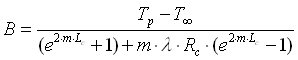
e sostituendo nella 25:
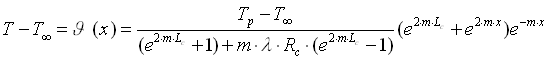
In questa equazione si nota chiaramente che m ha le dimensioni di una lunghezza (l’esponente è adimensionale).
Calcoliamo quindi la potenza scambiata per convezione dall’aletta:
![]()
sostituendo la 31 nella 32 e calcolando l’integrale si ottiene:
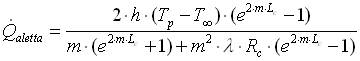
Notiamo che se l’aletta fosse stata ottenuta dal dispositivo per fusione avremmo avuto Rc = 0 ed il risultato sarebbe molto semplificato.
Guadagno ed efficienza di un’aletta
Possiamo ora confrontare la potenza scambiata dall’aletta con due altre potenze termiche:
Avremo:
![]() ( 34 )
( 34 )
Come avevamo gia visto l’efficienza dell’aletta ![]() sarà:
sarà:
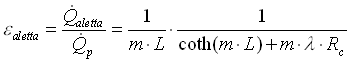 ( 36 )
( 36 )
Si definisce invece G guadagno dell’ aletta il rapporto :
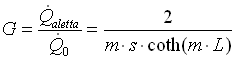
I guadagno è un fattore molto significativo, sempre maggiore di 1, che dice quanto lo scambio termico e aumentato nella zona in cui l’aletta è stata istallata.
Al crescere della costante di estinzione del’onda m efficienza e guadagno diminuiscono e viceversa.
Ricordando che :
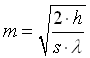 ( 38 )
( 38 )
Efficienza e guadagno aumentano con scarsi coefficienti di convezione h, buoni coefficienti di conducibilità termica λ e con l’aumento dello spessore dell’aletta s.
Bisogna dunque bilanciare L e l ed s per ottenere col materiale e lo spazio a disposizione il minimo valore di m.
Per un’aletta non ricavata per fusione dal componente stesso, minore è la resistenza di contatto Rc migliore è il rendimento della stessa.
In genere le alette non hanno mai un’efficienza inferiore al 40%.
Esistono dei diagrammi che mostrano l' efficienza dell' aletta in funzione di un rapporto adimensionale, per esempio fra la lunghezza e la superficie, o anche di rapporti più complessi (usati per alette non diritte); si tratta di diagrammi sperimentali che mettono in evidenza l’efficienza dell’aletta in funzione della sua geometria.
Ne riportiamo di seguito alcuni esempi:
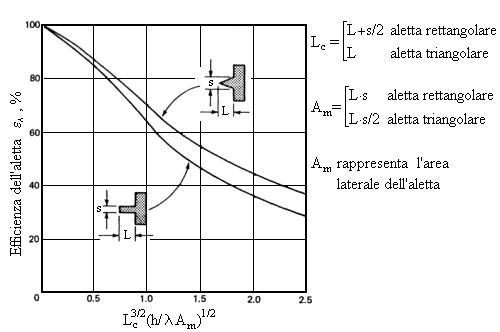
Fig. 14 – Efficienza comparata dell’aletta rettangolare e triangolare
Come si può notare dalla figura le alette triangolare sono più efficienti di quelle rettangolari, quindi rastremare alla punta le alette ne aumenta il rendimento. Nelle ascisse è riportato il parametro F è indicato come
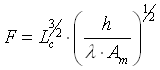 ( 39 )
( 39 )
dove sono gia noti tutti i termini tranne Am che però è indicato in figura e rappresenta l’area della sezione laterale dell’aletta.
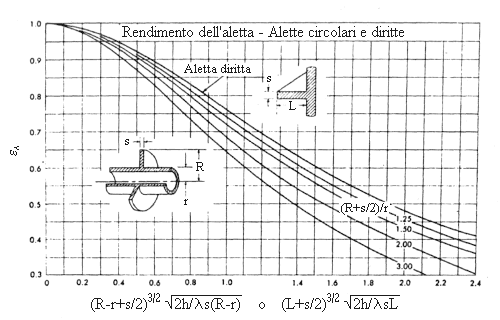
Fig. 15 - Efficienza comparata dell’aletta rettangolare e circolare
Questo grafico mette a confronto a quelle diritte un altro tipo di alette: le alette circolari.
Tali tipi di alette sono utilizzate ad esempio per raffreddare delle resistenze, o per riscaldare l’aria nei convettori, dotare una resistenza di un alettatura di questo tipo impedisce il surriscaldamento della stessa e ne aumenta la durata nel tempo.
Grafici di questo tipo sono di solito forniti dai costruttori di alettature commerciali e distribuiti all’acquisto, questi servono ad indicare quanto sarà il rendimento dell’alettatura acquistata, che avendo geometria fissa sarà in funzione del solo coefficiente di convezione, infatti l’unico parametro che il costruttore non può conoscere è il coefficiente di convezione h. Questi grafici quindi servono a dare un idea al possessore dell’alettatura del range di funzionamento della stessa. Se si ha un alettatura insufficiente all’utilizzo per cui e destinata non sempre può aiutare aumentare l’aria soffiata su di essa, facendo ciò l’alettatura potrebbe andare in crisi per quanto riguarda la conduzione della stessa, l’aletta rimane fredda e non scambia alcun calore. Abbiamo visto infatti che h compare, nell’equazione della costante di estinzione dell’onda m, al numeratore ossia all’aumentare di h l’efficienza diminuisce, tali grafici ci mostrano i valori su cui h può variare mantenendo l’efficienza ottimale.
In una prima ipotesi nelle zone non alettate si suppone che lo scambio termico avvenga come se le alette non ci fossero, tale ipotesi è vera in condizione di convezione forzata, ma non in condizione di convezione naturale, in tal caso è determinante anche la posizione in cui è collocato il dissipatore, per esempio se le alette sono rivolte verso il basso lo scambio termico viene fortemente limitato.
Efficienza dell’ alettatura
L’efficienza dell’alettatura sarà la potenza scambiata in totale dalle alette fratto la potenza scambiata dalle alette se fossero tutte alla temperatura di parete:
 ( 40 )
( 40 )
la potenza scambiata dalle alette può essere scritta come somma tra la potenza scambiata dalla superficie non alettata e la potenza scambiata dalle alette, si può scrivere anche:
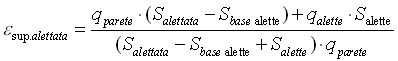 ( 41 )
( 41 )
e ricordando che:
![]() ( 42 )
( 42 )
![]()
otteniamo che:
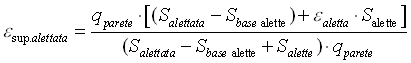 ( 44 )
( 44 )
e semplificando:
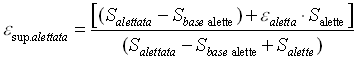 ( 45 )
( 45 )
Tale equazione ci dice che l’efficienza dell’alettatura è sempre maggiore dell’efficienza della singola aletta, e che maggiore è la superficie non alettata maggiore è l’efficienza della stessa, non sempre una superficie con molte alette ha un migliore rendimento rispetto ad una che ne ha di meno.
Esercizio: Dissipazione del calore di una CPU
Un processore quadrato di lato L è posto in una scheda madre in posizione verticale. La potenza da dissipare è ![]() e la temperatura dell’ambiente è T∞,vogliamo determinare un dispositivo sufficiente che, in condizioni di convezione naturale, faccia lavorare la CPU ad una temperatura adeguata (circa 100°C).
e la temperatura dell’ambiente è T∞,vogliamo determinare un dispositivo sufficiente che, in condizioni di convezione naturale, faccia lavorare la CPU ad una temperatura adeguata (circa 100°C).
Cominciamo a capire a che temperatura si porta il processore senza alcun dissipatore:
 Fig. 16 – CPU
Fig. 16 – CPU
·
L = 50 mm·
·
T∞ = 20 °CPer trovare la temperatura della CPU trascuriamo il calore dissipato dal contatto con la main board, il calore è scambiato per sola convezione. Ricordando che S = L2 possiamo utilizzare la 1:
![]() ( 46 )
( 46 )
bisogna però conoscere il coefficiente di convezione hc, che può essere ricavato da:
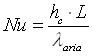
per ricavare il numero di Nusselt Nu, bisogna però ottenere il numero di Grashof Gr, la cui espressione è data da
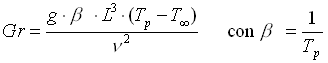 ( 48 )
( 48 )
Dove g è la gravità, β il coefficiente di dilatazione termica (inverso della temperatura per i gas), υ la viscosità cinematica dell' aria. Bisogna imporre a questo punto un’adeguata temperatura alla parete, solo in una prima analisi, per poter fare il calcolo, ipotizziamo Tp = 100°C. La 48 diventa:
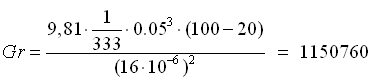 ( 49 )
( 49 )
in questo caso il numero di Prandtl Pr è circa 0.71, si ottiene perciò che il numero di Raleigh Ra è:
![]() ( 50 )
( 50 )
In conseguenza del fatto che Ra << 109, possiamo affermare che ci troviamo in regime di moto laminare, dalla tabella delle formule sperimentali per il calcolo del numero di Nusselt Nu troviamo che i coefficienti a e b sono pari a 0.25, per cui:
![]() ( 51 )
( 51 )
perciò dalla 47, ricordando che λ aria secca = 0.026 W/mK, ricaviamo:
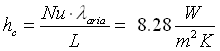 ( 52 )
( 52 )
e dalla 46 si può trovare finalmente la temperatura della CPU:
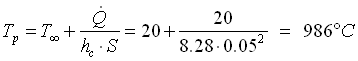 ( 53 )
( 53 )
Con questa temperatura qualunque componente elettronico brucerebbe in pochi istanti, anche se, probabilmente, il fatto di aver trascurato lo scambio termico per irraggiamento ha sfalsato il risultato. Proviamo quindi ad averne conto calcolando il coefficiente di irraggiamento hr:
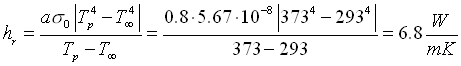 ( 54 )
( 54 )
dove a è il coefficiente di assorbimento del materiale (in genere plastica nera), e σ è la costante di Stefan-Boltzmann.
Il coefficiente totale allora sarà:
![]() ( 55 )
( 55 )
percio la temperatura di parete sarà:
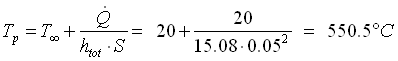 ( 56 )
( 56 )
che è ancora una temperatura troppo alta per una CPU.
Occorre dunque dotare il processore di un dispositivo per la dissipazione del calore come una superficie alettata.
Prendiamo ad esempio una superficie alettata in alluminio composta da otto alette di spessore s e lunghezza Laletta disposte come in figura:
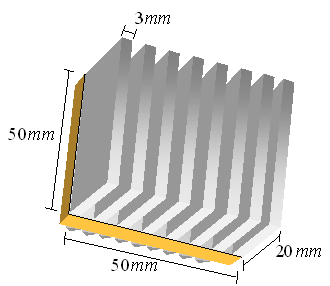
Fig. 16 – CPU sormontata da una superficie alettata
Con :
La superficie non alettata Sparete può essere calcolata come quella totale della CPU diminuita di quella occupata dalla base delle alette:
![]() ( 57 )
( 57 )
mentre la superficie totale Salette delle alette è :
![]()
Per calcolare la temperatura possiamo utilizzare questa formula:
![]() ( 59 )
( 59 )
abbiamo considerato il solo coefficiente di convezione hc perché in questo caso oltre al fatto che le alette sono poste l’una al fianco dell’altra, il materiale di cui sono fatte è alluminio lucido che ha un coefficiente di assorbimento molto più piccolo di quello della plastica nera di cui è composta la CPU, perciò lo scambio termico per irraggiamento e da considerarsi trascurabile.
Nell’ equazione 59 l’unico parametro rimasto da calcolare è l’efficienza dell’aletta εaletta. Possiamo procedere in due modi, con l’equazione 36 che ci da direttamente l’efficienza, o con l’equazione 39 con cui grazie al grafico in figura 14 arriviamo al risultato cercato. Proseguiamo con entrambi.
Ricordiamo la 36 semplificata (ossia ponendo nulla la resistenza di contatto Rc):
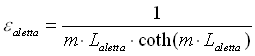 ( 60 )
( 60 )
dalla 38 calcoliamo m :
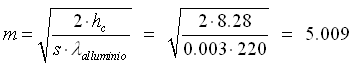 ( 61 )
( 61 )
e dalla 60 otteniamo che l’efficienza è del 99%. Tale valore è un po’ troppo alto (ma ricordiamo che abbiamo trascurato la resistenza di contatto), proviamo a verificarlo con il secondo metodo; il parametro F è dato dalla 39:
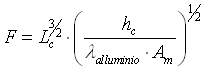 ( 62 )
( 62 )
Calcoliamo i parametri che occorrono:
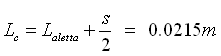
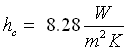
allora sarà: F = 0.08.
Dal grafico della figura 14 possiamo quindi trovare l’efficienza dell’aletta che calcoliamo, anche questa volta, pari a circa il 98-99% . Tenendo presente che anche col metodo presente εaletta era del 99% e che abbiamo detto che una tale efficienza ci sembrava esagerata poniamo εaletta = 98%.
Infine dalla 59 ricaviamo:
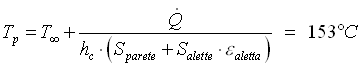 ( 63 )
( 63 )
che è ancora troppo alta!!
Proviamo ad aumentare la lunghezza delle alette, poniamo :
In questo abbiamo un dissipatore di forma cubica, ciò è abbastanza comune nei dissipatori per processori, avremo quindi:
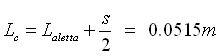
e quindi F = 0.18 e l’efficienza εaletta è del 96%. Anche se l’efficienza della singola aletta è diminuita l’aumento della superficie delle alette Salette ne contrasta l’effetto (vedi equazione 63), portando ad una diminuzione della temperatura.
L’ultimo parametro da calcolare è quindi la superficie delle alette:
e quindi dalla 63 abbiamo che Tp = 79°C.
Come previsto la temperatura della CPU è diminuita ben al di sotto dei 100°C. Ciò dimostra che il dispositivo appena studiato è ampiamente sufficiente. Bisogna comunque ricordare che abbiamo trascurato la resistenza di contatto dovuta al fatto che il dissipatore è comunemente appoggiato sul processore, ed anche che all’inizio dei nostri calcoli abbiamo dovuto ipotizzare una temperatura della CPU di 100°C per poter calcolare il numero di Grashof, si potrebbe quindi ripetere l’esercizio considerando la resistenza di contatto e mettendo nel computo del numero di Grashof la temperatura ottenuta nell’esercizio appena svolto. Ripetendo quest’ultima operazione più volte il risultato sarà sempre più vicino alla temperatura realmente raggiunta dalla CPU.
Considerazioni
Dall’esercizio appena svolto nascono alcuni spunti per delle considerazioni:
Abbiamo visto che per ottenere una migliore dissipazione del calore si è dovuta aumentare la lunghezza dell’aletta a scapito del suo rendimento, operato che a prima vista sembrerebbe controproducente ma che come dimostrato ha portato al risultato voluto. Ma allora qual’è il parametro più importante al fine di raggiungere il fine preposto ? Cerchiamo di rispondere a questa domanda osservando i seguenti grafici:
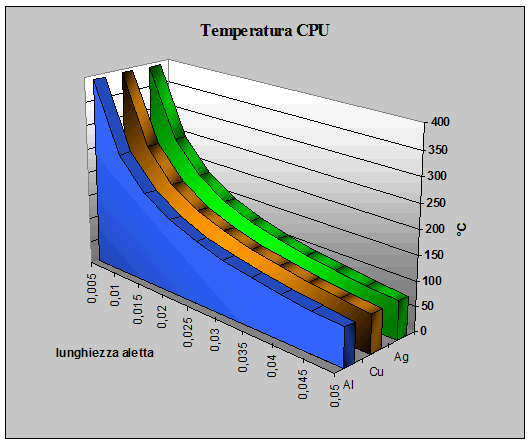
Fig. 17 - Grafico della temperatura in funzione della
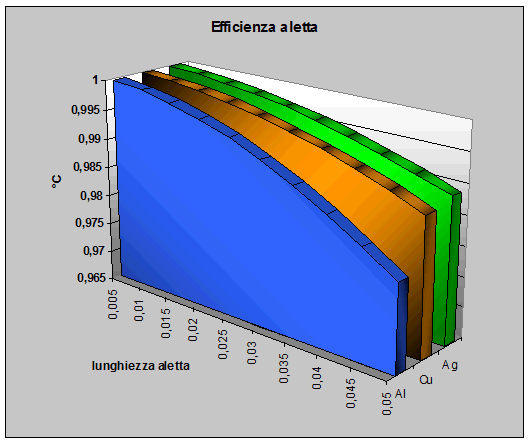
Fig. 18 – Efficienza dell’aletta in funzione della sua lunghezza
Come si nota dai grafici, all’aumentare della lunghezza dell’aletta, l’efficienza, diminuisce. Ciò accade però in maniera diversa tra i tre materiali scelti come esempio (Argento, Rame, Alluminio) infatti mentre per l’argento l’efficienza cala dal 99,9% a 98,9% ossia dell’ 1% per l’alluminio si passa da 99,9% a 97,9% con una variazione del 2%, tale differenza però non è minimamente avvertita dalla temperatura raggiunta dalla CPU, infatti con lo stesso ragionamento fatto sopra per l’alluminio si va da 391.67°C a 77.98°C con un salto di 313,69°C mentre per l’argento da 391,64°C a 77.43°C con una differenza di 314,21°C. La differenza tra i due scarti (314,21°C e 313,69°C) è di 0.52°C che è ben al disotto dell’1% rilevato tra le efficienze! Ciò sta a significare che il parametro più importante, tenendo costanti numero e forma delle alette e coefficiente di convezione, è la lunghezza delle alette ossia la superficie di scambio del calore. Si può avere conferma delle considerazioni fatte e farne anche delle altre con il foglio di lavoro in Excel riportato di seguito:
 Fig. 19 – Cartella di lavoro di Microsoft Excel
Fig. 19 – Cartella di lavoro di Microsoft Excel
All’interno di esso troverete il calcolo automatico dell’efficienza e della temperatura di un dissipatore a base quadrata, in funzione al materiale usato e alla lunghezza delle alette, i valori messi di default sono quelli riportati nell’esercizio ma possono essere cambiati in modo da sperimentare diverse geometrie o simulare la forzatura dell’aria (aumentando il coefficiente di convezione) o variare il numero delle alette e il loro spessore (fare attenzione ai commenti).