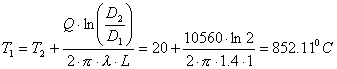Esercizi da esame

UNIVERSITA’ DEGLI STUDI DI PARMA

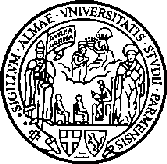
Anno accademico 2001-2002

Corso di laurea : ingegneria delle telecomunicazioni

 

Corso di fisica tecnica

Docente del corso : Angelo Farina

Relazione della lezione di fisica tecnica tenuta

 il giorno 18/12/2001 alle ore

16 :30-18 :30

 

 

 

In questa ultima lezione dell’anno accademico, abbiamo svolto degli esercizi d’esami degli ultimi appelli.

In seguito riporteremo l’originale del testo d’esame con la particolare personalizzazione dei dati a seconda del numero di matricola, e svolgeremo l’esercizio riferendoci al particolare numero 123456.

 

Nota: 
La personalizzazione dei dati di ingresso in funzione del numero di matricola è fatta assegnando una opportuna variabile intera a ciascuna cifra del numero, con nome letterale A,B,C,D,E,F. Ad esempio, il numero di matricola 128674 dà luogo ad A=1, B=2, C=8, D=6, E=7, F=4. I dati del problema sono assegnati in funzione di tali variabili, che possono venire giustapposte onde ottenere numeri con più di una cifra. Esempi:

Lunghezza = 3 + 0.5*C (m) = 3 + 0.5 * 8 = 7 m

Massa = 0.27+0.05 * DE (kg) = 0.27 + 0.05 * 67 = 3.62 kg 

Si noti che DE non significa D * E, quindi DE = 67, e non 6*7=42

Si noti infine che gli esercizi d'esame solitamente NON SONO SIMILI a quelli già svolti a lezione e riportati nelle dispense, per cui lo studente deve impostare la soluzione ex-novo, e non cercare affannosamente negli appunti un esercizio similare già svolto. Spesso anzi così facendo si viene tratti in inganno, perchè l'esercizio d'esame può apparire simile ad uno già svolto, MA IN REALTA' E' DIVERSO (solitamente più facile).

 

 

 

Esame 24 del  14/09/2001

1° Esercizio – Termodinamica (tolleranza +/- 10%)

 

Due correnti di aria umida confluiscono in un collettore, da cui fuoriesce una terza corrente miscelata. Non si hanno scambi termici o di lavoro con l'esterno. Note le proprietà delle due correnti in ingresso, determinare le proprietà della corrente in uscita.

Portate in massa in ingresso Ma1 = 2+0.1*F = 2.6 kg/s

                                                Ma2 = 1+0.2*E  = 2   kg/s

Temperature in ingresso          T1 = 30+D = 34  °C

                                                 T2 = 10+C =13  °C              

Gradi igrometrici                      1 = 0.1+0.09*C = 0.37

                                          *2 = 0.2+0.02*B =  0.24

 

Determinare:

- Grado igrometrico corrente di uscita                      ____                               (3 punti)

 

- Temperatura corrente di uscita                                  ____    °C                   (3 punti)

 

 

 

 

 

 

 

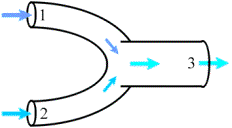
Osserviamo che il componente in esame è meccanicamente isolato ed adiabatico, quindi Q=0, L=0

 

Ma3 = Ma1+ Ma 2 = 4.6 kg/s

 

Calcolo ora i titoli delle correnti d’aria umida in ingresso:

 

   

 

      

 

dove  e  sono  le pressioni di saturazione dell’aria umida alle temperature di 34°C e 13°C  rispettivamente.

Il bilancio energetico mi dice che:

 

 H3= H1 +H2         Ma3J 3 = Ma1J1+ Ma 2J2

 

E per calcolare l’entalpia specifica J 3 prima devo trovare il titolo nella sezione 3 sfruttando l’equazione del bilancio di massa  del vapore per un sistema aperto:

 

                                

 

 

 

inoltre sono in grado di calcolare le entalpie specifiche delle 2 sezioni d’ingresso:

 

 

 

                    

  ma posso sempre scrivere 

             e risolvendo questa equazione lineare di 1˚ grado ottengo 

 

Ora il calcolo della seconda incognita del problema risulta immediato:

 

      

 

dove ho preso dalle tabelle la pressione di saturazione

 

 

 

2° Esercizio – Fluidodinamica (tolleranza +/- 20%)

 

Trovare lo sforzo risultante esercitato dal vento alla base dei pali di una linea telefonica, nell’ipotesi che lo stesso soffi in direzione ortogonale alla linea. I pali sono alti 12m e distano l’uno dall’altro 60m, e la velocità del vento è di 10 m/s.

Diametro del cavo telefonico        D1    =2+0.02*BC = 2.46  mm         

Diametro del palo di sostegno       D2 =50+EF = 0.106  m

Temperatura dell’aria                      T=010+CD/4 = 18.5  °C

Determinare:

- Forza applicata dal filo al palo                       _____     N                  (3 punti)

 

- Forza complessiva alla base del palo             _____     N                  (3 punti)

 

 

 

 

 

Le due equazioni che mi serviranno per calcolare la forza applicata dal filo al palo e la forza alla base del palo  (F1 e F2  rispettivamente) sono:

dove  e sono i coefficienti di penetrazione del filo e del palo, mentre  e  sono le loro aree frontali e  è la densità dell’aria che calcolo come:

 

                            

 

ricordando che la pressione atmosferica media al livello del mare è 101325 Pa.

 

 

Posso trovare i coefficienti di resistenza CR dal diagramma seguente, che richiede la conoscenza del numero di Reynolds nei 2 casi:

 

            CR1 = 0.99

            CR2 = 1.2

 

 

 

 

Coefficiente di resistenza di cilindro investito normalmente da una corrente piana uniforme

 

 

Ora sostituendo i valori trovati nelle equazioni iniziali trovo le incognite del problema:

 

 

FTOT= F1+F2 = 96.09 N

 

 

 

 

 

3° Esercizio – Acustica (tolleranza +/- 0.5 dB)

Una sorgente di rumore incoerente in banda larga, puntiforme ed omnidirezionale ha livello di potenza pari a 90+C dB. Essa è situata entro un ambiente semiriverberante Sabiniano, avente un volume pari a 400+20·B m3, con superficie interna pari a 350+20·E m2, che ha coeff. di assorbimento pari a 0.2 + EF/200. Trovare il tempo di riverberazione ed il livello sonoro in un punto posto entro l’ambiente, e distante 5m dalla sorgente.

 

 

 dB

V = 440 m3

S = 450  m2

     

 Determinare:

-   Tempo di riverberazione                                          _____  s         

 

-  Livello complessivo lineare                                    _____ dB                      

 



La prima parte è di immediata risoluzione applicando la formula di  Sabin:

 

 

osservo che il tempo di riverberazione è molto piccolo, deduco che mi trovo in un ambiente molto assorbente, dove potrei probabilmente trascurare l’effetto dell’onda riverberante, ma per sicurezza risolviamo il problema utilizzando la legge che descrive l’andamento del livello sonoro in un campo semiriverberante:

 

 

 

 

dove il fattore di direttività è Q=1 essendo la sorgente omnidirezionale.

Osservo che se non avessi considerato il contributo del suono riverberante, avrei ottenuto un risultato di , al di fuori quindi della tolleranza di  data dal testo.

 

 

 

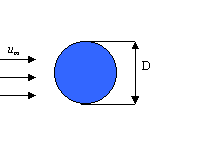
4° Esercizio – Termocinetica (tolleranza +/- 20%)

 

Una sfera di acciaio, con diametro pari a 50 + CD mm, si trova inizialmente alla temperatura di 300+EF °C. Essa viene raffreddata mediante aria avente temperatura di 20 + B °C, e velocità di 12+C m/s. Trovare il tempo necessario affinché la sfera di acciaio raggiunga la temperatura superficiale di 60 °C.

Determinare:

- Coeff. di convezione                            ________                  W/m2K                     

- Tempo di raffreddamento                   ________                   s        

 

 

D = 84 mm

 

    

 

Considero un intervallo di tempo infinitesimo e confronto la situazione del sistema all’istante  ed all’istante  + :

In   il sistema aveva un’energia

   che viene gradualmente ceduta all’ambiente esterno tramite scambio convettivo, allora:

                      inoltre posso scrivere

                e mettendo a sistema queste due equazioni ottengo un’equazione differenziale del primo ordine a variabili separabili.

   che integrata da:

 

       

 

ora trovo il coefficiente di convezione h ricordando che siamo in regime di convezione forzata con un flusso d’aria che soffia contro una sfera

 

 

             con  calcolata ad una temperatura media tra quella della sfera e quella dell’aria,considerata

ora posso usare anche la formula:

 

 

e ottengo l’incognita h dalla formula:

 

e da qui ricavo , ricordando che e il volume della sfera è

 

 

 

 

 

 

 

Esame 22 del 12/07/2001

1° Esercizio – Termodinamica (tolleranza +/- 10%)

In un ambiente è contenuta aria umida, alla temperatura di 20+E °C e grado igrometrico pari a 0.3+F/20. La temperatura viene ridotta, a titolo costante, sino al punto di rugiada. Determinare la quantità di calore sottratta per kg di aria secca.

 

- Temperatura di rugiada                     _______                     °C                   (3 punti)

 

- Calore sottratto                                 _______                     kJ/kga              (3 punti)

 

 

 

 

 

Trovo inizialmente il titolo:

 e osservando che il titolo resta costante fino al punto di rugiada dove

               

dove abbiamo ottenuto il valore di   dalle tabelle del vapor d’acqua.

               

 

 

 

 

 

 

 

 

 

 

2° Esercizio – Fluidodinamica (tolleranza +/- 10%)

Un serbatoio di forma cilindrica ha un diametro di 2+0.1*F m e contiene acqua mantenuta ad un livello di 4 + D m. Sul fondo di esso  si trova un foro circolare a spigoli vivi (β = 1), con diametro pari ad 1/20 di quello del serbatoio, per cui l’acqua comincia ad uscire. Determinare la velocità e la portata in massa del getto di acqua che fuoriesce.

- Velocità di uscita W2       _______               m/s                              (3 punti)

 

- Portata in massa Qm         _______              kg/s                             (3 punti)

 

 

 

 

 

 

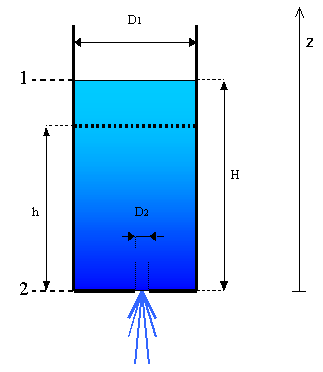
osservo subito che il diametro del foro è molto minore del diametro del serbatoio, allora posso considerare con buona approssimazione l’altezza H del livello dell’acqua costante a 8m; poi scrivo l’eq. del bilancio energetico:

                  

mentre la portata in massa  dipende dal diametro del foro,infatti

               dove  è la superficie del foro

            e sostituendo:

     Kg/s

 

 

 

3° Esercizio – Acustica (tolleranza +/- 1 dB e +/- 0.05)

Entro un tubo ad onde stazionarie (tubo di Kundt), eccitato con un tono puro a 1000 Hz, si misura un livello di intensità sonora pari a 80+C dB, ed un livello di densità dell’energia sonora pari a 85+C dB. Determinare il livello massimo di pressione ed il coeff. di assorbimento del materiale posto all’estremità del tubo.

 

-  Livello max di pressione               ______                 dB                               (3 punti)

 

-  Coeff. di assorbimento               ______                                                      (3 punti)

 

 

 

 

 

 

 

 

 

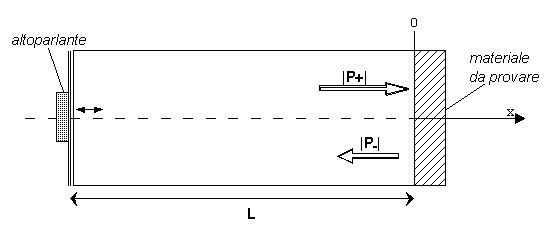
Dato che in tutti i punti del tubo i livelli di intensità sonora e d’energia sonora sono costanti, allora posso ricavare il coefficiente d’assorbimento:

 

                                     dove r è il coefficiente di riflessione

 

imposto ora un sistema in 2 equazioni per calcolare le 2 incognite  e :

  : sotraggo le 2 intensità perché le onde hanno versi  discordi

 

 

dove in generale e  

 

               = 0.00041524     

                    0.00021572

 

 

 

 

Sappiamo che in tubo di Kundt la pressione ha un andamento oscillatorio con massimi e minimi, come in figura

 

 

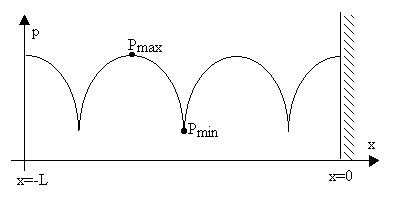
Un primo modo per trovare il livello massimo di pressione è:

 

 

 

 

 

 

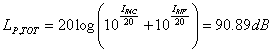
un’ulteriore modo è:

                  

                                    

 

 

 

 

 

4° Esercizio – Termocinetica (tolleranza +/- 10%)

 

Dentro una tubo lungo 1 m, in materiale ceramico, una resistenza elettrica genera calore per effetto Joule. La potenza generata è pari a 10000+EF*10 W. Il diametro interno del tubo è 0.02+C/100 m, quello esterno è il doppio. La conducibilità del materiale è pari a 1+0.1*D W/mK. La parete esterna è mantenuta a 20°C. Determinare la temperatura della parete interna.

 

- Resistenza termica del tubo                ______         K/W                              (3 punti)

 

- Temperatura parete interna                ______                   °C                        (3 punti)

 

    

 

ci troviamo in una situazione dove lo scambio termico avviene per conduzione quindi la resistenza termica del tubo risulta essere:

 

 

 

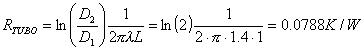
Mentre ottengo la temperatura della parete interna invertendo: