F
L U I D O D I N A M I C A
1. INTRODUZIONE
La FLUIDODINAMICA studia il movimento dei fluidi sia quando essi si trovino all’interno di un condotto (MOTO INTERNO) sia nel caso lambiscano un solido (MOTO ESTERNO).
Per fluido si intende l’insieme delle sostanze LIQUIDE (quelle con volume proprio ma che assumono la forma del recipiente in cui sono contenute) e delle sostanze AERIFORMI (quelle che tendono ad occupare tutto il volume a loro disposizione).
Di seguito si tratterà il moto interno, considerando condotti lisci a sezione circolare, assumendo l’IPOTESI DELL’ADERENZA: le particelle di fluido a contatto con la parete del condotto aderiscono con essa, cioè la loro velocità (in direzione tangenziale rispetto al condotto) in quei punti è nulla. Non appena ci si allontana dalla parete la velocità del fluido non è più nulla. Questa caratteristica dei fluidi è dovuta alla loro natura viscosa, cioè agli attriti interni che influisco sulla capacità dei fluidi di scorrere.
2. PROVA DI COMPRESSIONE
Questa prova, schematizzata nella figura 1, ci da una indicazione sull’elasticità di un materiale. Essa consiste nello schiacciare un provino di materiale in una pressa (una volta nel caso di prova statica, con un carico oscillante nella prova dinamica). Se, tolto il carico il materia ritorna nella sua forma iniziale ripercorrendo la stessa curva (in figura 2 indicata con a) nel diagramma di carico (x,F) esso si dirà elastico in quanto in grado di restituire tutta l’energia data senza dissipazioni. Quindi un materiale elastico è perfettamente conservativo energeticamente.
Se invece si tratta di un materiale viscoelastico la curva di ritorno sarà quella indicata con b, e si avranno delle perdite. L’energia dissipata è l’area colorata di blu, si può quindi calcolare un fattore di perdita η rispetto all’energia totale Etot (l’area blu più l’area rossa, vedi 2.1) data al corpo.
Infine se il materiale è puramente viscoso, cioè non elastico, la deformazione rimane anche dopo aver tolto il carico.
Questa proprietà dipende dall’entità della forza di compressione come si mostra in figura 3.
(2.1) 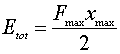
(2.2) 
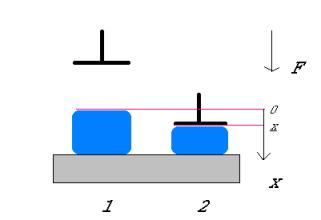 Figura 1
Figura 1
 Figura 2
Figura 2
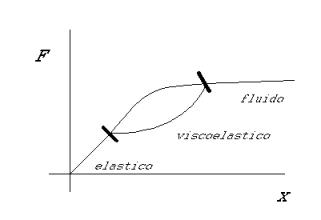 Figura 3
Figura 3
3. VISCOSIMETRO A ROTAZIONE
Durante lo scorrimento di un fluido tra i suoi vari strati si formano degli attriti che si oppongono allo scorrimento. L’insieme di queste forze è detto sforzo di trascinamento, oppure se considerate per unità di superficie si dicono tensioni tangenziali e indicate con la lettera greca τ.
Per misurare sperimentalmente questa costante si usano diversi metodi: viscosimetri a capillare, viscosimetri a caduta di solido, viscosimetri basati sullo sforzo tangenziale esercitato dal liquido su un solido in rotazione. Osserviamo quest’ultimo tipo nella figura 4 e schematizzato nella figura 5.
 Figura 4
Figura 4
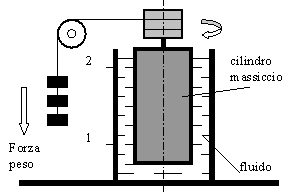 Figura 5
Figura 5
All’interno di un cilindro cavo, mantenuto a temperatura costante, contenente il liquido in esame, vi è, coassiale, un secondo cilindro massiccio, che può essere tenuto in rotazione intorno al suo asse da un momento motore, fornito da una serie di pesi che esercitano la loro forza su una funicella avvolta da una puleggia. Si deve misurare la differenza tra il momento motore necessario a produrre la rotazione del cilindro interno, quando il livello del liquido è in 1e quando il livello è in 2: la velocità di rotazione deve ovviamente essere la stessa. Dalla differenza dei due momenti si può risalire al valore della viscosità (vedi formula 3.1).
(3.1) ![]()
(con M = momento, f = sforzo di trascinamento, R = raggio cilindro interno, H = altezza liquido, τ = tensioni tangenziali, S = superficie cilindro interno bagnata)
4. LEGGE DI NEWTON
(4.1) 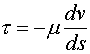
![]()
Secondo questa legge c’è una proporzionalità diretta tra la variazione della velocità del fluido lungo l’asse radiale del condotto in cui scorre e le tensioni tangenziali.
Il coefficiente di proporzionalità è detto viscosità dinamica e dipende dalla temperatura.
I fluidi che rispettano questa legge sono detti newtoniani (come l’aria, l’acqua , l’olio d’oliva, l’olio motore…), quelli con una caratteristica (dv/ds,τ) che resta sotto la retta di Newton sono detti pseudoplastici, i restanti vengono chiamati dilatanti.
Se rapportato alla densità del fluido è detto viscosità cinetica.
(4.2) 
![]()
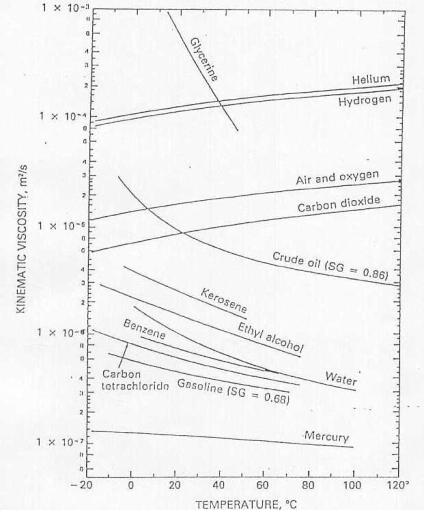
Di seguito le tabelle (T,ν) e (T,μ) di alcuni fluidi

5. VELOCITA’ RADIALE
Voglio ora determinare la velocità del fluido Vx in una sezione x del condotto (un tubo liscio, di sezione A, circolare, con raggio R di lunghezza l ) in funzione del raggio r (di cui considero l’origine il centro del condotto).
La differenza di pressione tra le 2
estremità del tubo genera una forza che spinge il fluido a scorrere. A regime,
in condizioni stazionarie, questa forza deve vincere la forza dovuta alle
tensioni tangenziali che si oppongono allo scorrimento del fluido. Bilanciando le forze in gioco si ha:
(5.1) ![]()
(5.2) ![]()
esplicitando l’area della sezione e la superficie di contatto tra fluido e condotto
(5.3) ![]()
semplificando e applicando la legge di Newton
(5.4) ![]()
(5.5) ![]()
integrando da un punto qualsiasi del tubo alla parete di esso
(5.6) ![]()
risolvendo gli integrali
(5.7) ![]()
sostituendo
(5.8) ![]()
esplicitando la velocità
(5.9) ![]()
sostituendo a r 0 posso trovare la velocità massima nel condotto
(5.10) ![]()
6. VELOCITA’
MEDIA
La velocità media w è definita come la portata in
volume in una certa sezione del condotto diviso la sezione del condotto, ma è
preferibile esprimerla in funzione della portata in massa e della densità in quanto in regime stazionario la
conservazione della portata massa vale sempre (portata in massa in ingresso =
portata in massa in uscita), la conservazione della portata in volume si verifica
solo se il fluido è incomprimibile (cioè densità costante).Quindi indicando con
w la velocità media, A la sezione del condotto, ![]() la portata in massa,
la portata in massa, ![]() la portata in volume,
ρ la densità si ha:
la portata in volume,
ρ la densità si ha:
(6.1) 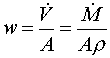
Se invece si opera la media della funzione v(r) a densità costante e a densità non costante rispetto alla sezione si ottiene:
(6.2a,b) 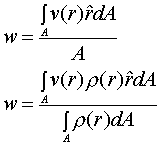
Ora, andando a sostituire nell’equazione (6.2a) la funzione v(r) trovata precedentemente
(6.3) 
Risolvendo l’integrale e semplificando
(6.4) 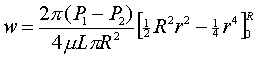
(6.5) 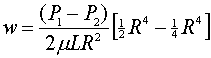
(6.6) 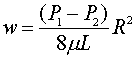
Nella realtà la rilevazione della velocità media deve avvenire con una serie di misure avendo diviso la sezione in questione in una ideale griglia e utilizzando l’equazione integrale (6.2b). Questa misurazione è essere necessaria ad esempio nel collaudo di un sistema di aerazione degli edifici pubblici in quanto il ricambio d’aria è fissato per legge (per il comune di Parma : 2 VOLUMI/ORA)
7. EQUAZIONI FONDAMENTALI
Problemi tipici della fluidodinamica sono la progettazione e il dimensionamento di condotti in cui si sfrutta la forza di gravità o sistemi in cui si deve superare un dislivello utilizzando il salto di pressione dato da una pompa.
Le equazioni che ci permetto di risolvere questi problemi sono:
l’equazione di conservazione della massa (costante nelle ipotesi di regime stazionario e trascurando accumuli e svuotamenti interni)
(7.1) ![]()
e l’equazione di bilancio dell’energia del sistemi aperti (la somma dell’energia cinetica, dell’energia potenziale, del salto di entalpia è uguale alla differenza tra calore e lavoro scambiati)
(7.2) ![]()
Riferendoci a grandezze specifiche riferite all’unità di massa;
considerando solo fenomeni isotermi (nei quali il fluido non cambia temperatura) per cui si ha che:
(7.2.1) ![]() ;
;
considerando sistemi con volumi specifici costanti (e densità costanti), ad energia interna costante rispetto alla temperatura tali che il salto di entalpia diventi:
(7.2.2)  ;
;
considerando una perdita di energia R dovuta al calore dissipato all’interno del fluido;
individuando un punto 1 con velocità w1 un’altezza z1 e una pressione p1
e un punto 2 con velocità w2
un’altezza z2 e una pressione p2;
l’equazione diventa
(7.3) 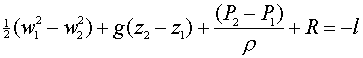
Tutti i termini sono espressi in joule su chilogrammi.
8. PREVALENZA
La prevalenza è la differenza di pressione che una pompa deve superare per sollevare un liquido da un serbatoio ad un altro situato ad un livello superiore.
Applicando l’equazione del bilancio dell’energia (7.3) ai punti di ingresso e di uscita della pompa, trascurando la differenza di velocità, di pendenza e le perdite di energia
Si ottiene la relazione
(8.1) ![]()
![]()