

UNIVERSITA’ DEGLI STUDI DI PARMA
Facoltà di Ingegneria
Corso di Laurea in Ingegneria Elettronica
Anno 2000/2001
FISICA TECNICA
Docente Prof. Ing. Angelo Farina
Studente :Zicari Gianluca matr.117877
ESERCIZI SULLA FLUIDODINAMICA
Introduzione
In questa tesina verranno analizzati alcuni tipi di esercizi sulla fluidodinamica (molti di questi sono stati temi d’esame relativi ad appelli precedenti) allo scopo di rendere più chiare tutte le problematiche in cui si incorre quando ci si trova a dover affrontare questi tipi di problemi. In particolare verrà messo in evidenza come in alcuni esercizi il calcolo di determinate variabili sarà reso possibile soltanto ricorrendo ad una metodologia per "tentativi", ma tutto apparirà più chiaro analizzando gli esempi proposti di seguito.
ESERCIZIO N.1
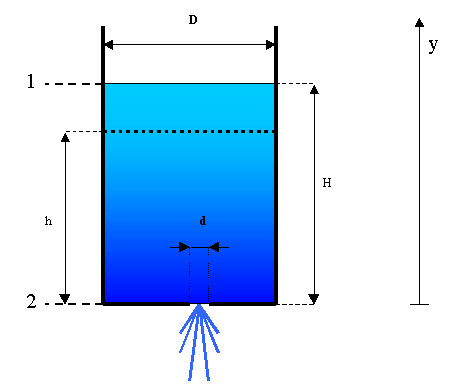
Si consideri un serbatoio di forma cilindrica contenente dell’acqua fino ad un livello pari a H. Supponendo che, sul fondo di esso vi sia un foro circolare (tale da introdurre un![]() ) il cui diametro è pari ad un ventesimo di quello del serbatoio ( per cui l’acqua comincia a fuoriuscire), si chiede di determinare il tempo
) il cui diametro è pari ad un ventesimo di quello del serbatoio ( per cui l’acqua comincia a fuoriuscire), si chiede di determinare il tempo ![]() necessario per il completo svuotamento del serbatoio .
necessario per il completo svuotamento del serbatoio .
ANALISI:
Come è ben evidenziato dal disegno è innanzitutto necessario scegliere opportunamente le sezioni cui riferirsi . Indicheremo con:
Si osserva che, essendoci un foro alla base del serbatoio, l’acqua comincerà a fuoriuscire da esso variando continuamente il suo livello. Tale diminuzione di quota (considerando l’asse y crescente verso l’alto), comporterà una conseguente diminuzione dell’energia potenziale. Per cui, preso ad esempio come posizione iniziale del pelo libero la quota z1=h e posizione finale allo sbocco la quota z2=0, si avrà chiaramente una variazione di quota negativa.
Applicando l’equazione di Bernoulli avremo che:
![]()
![]() (1)
(1)
Con le osservazioni appena fatte, avremo che z2-z1=-h dove h rappresenta la posizione generica del pelo libero in un certo istante di tempo.
Potremo quindi riscrivere la 1) nel seguente modo:
![]() (2)
(2)
Un ulteriore osservazione che è lecito fare ai fini di semplificare ulteriormente l’espressione ( 2) è la seguente:
Quindi scriveremo la 2) nel seguente modo:
![]() (3)
(3)
in cui ![]()
![]()
rappresenta le perdite di carico concentrate.
Pertanto scriveremo :
![]() (4)
(4)
Le incognite in questa equazione sono rappresentate da W1 e W2, ma in realtà il liquido è inizialmente fermo per cui W1=0.
La (4) allora diventa:
![]() (5)
(5)
nella sola incognita W2, da cui attraverso semplici passaggi algebrici è possibile esplicitarla come segue:
![]() (6)
(6)
Osservazione: la velocità cala con la radice quadrata del livello di liquido raggiunto nel serbatoio (che cala anch’esso!).
Il nostro scopo è quello di valutare la quantità di liquido ![]() che nel tempo
che nel tempo ![]() attraversa la superficie del foro.
attraversa la superficie del foro.
Ricordando che:
otteniamo ![]()
![]()
![]() (7)
(7)
Ma chi è ![]() ?
?
![]() è l’abbassamento del pelo libero (dimensionalmente è un volume) ed è uguale a:
è l’abbassamento del pelo libero (dimensionalmente è un volume) ed è uguale a:
![]() (8)
(8) ![]()
Uguagliando le due espressioni:![]()
![]() (9)
(9)
![]() -
-![]()
![]() (10)
(10)
Essendo h la posizione generica del pelo libero, i cui estremi variano tra H e 0, integrando la 10) otteniamo:
![]()
![]()
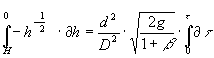
![]()
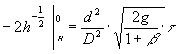
![]()
![]()
![]()
![]()
![]()
![]()
da cui il tempo di svuotamento sarà uguale a:
![]()
ESERCIZIO N.2
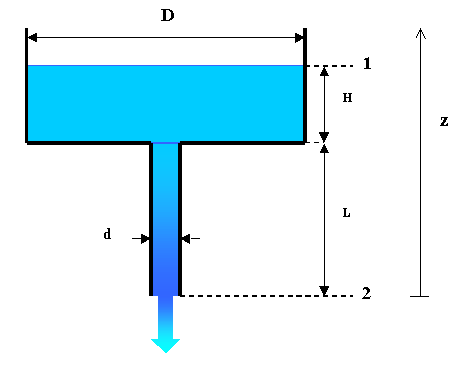
Anche in questo esercizio ( che è una variante a quello precedente) scegliamo come sezione n.1 quella al pelo libero e sezione n.2 quella allo sbocco del condotto. Varranno inoltre le stesse considerazioni fatte in precedenza per quanto concerne le pressioni ( P1=P2=P0), e la velocità al pelo libero (W1![]() ). Allo stesso modo avremo una variazione di quota del liquido negativa, poiché il serbatoio si sta svuotando. Ma allora cos’è che cambia?
). Allo stesso modo avremo una variazione di quota del liquido negativa, poiché il serbatoio si sta svuotando. Ma allora cos’è che cambia?
Come si può vedere dal disegno, adesso è collegato al serbatoio , un condotto di diametro nettamente inferiore e abbastanza lungo, tale da dover considerare non solo le perdite concentrate, ,ma anche quelle distribuite.
Scriviamo l’equazione del bilancio dell’energia:
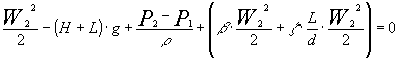 (11)
(11)
Osservazione: il secondo membro è nullo poiché non vi sono pompe o altre fonti di energia in grado di compiere lavoro sul sistema.
Dalla (11) tenendo conto che P2-P1=0, attraverso alcuni passaggi algebrici si giunge ad esplicitare la W2 come:
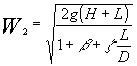 (12)
(12)
Mettiamoci nell’ipotesi di considerare un condotto molto lungo per cui si abbia :
![]()
Prendiamo un valore medio del tipo:
![]()
Per cui la (12) diventa:
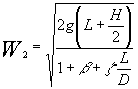 (13)
(13)
Dalla (13) osserviamo che la velocità dipende da ![]() , ma :
, ma :
![]() e
e ![]()
Quindi non conoscendo ![]() non possiamo trovare la velocità W2.
non possiamo trovare la velocità W2.
..e allora come facciamo?
In questi casi si ipotizza ad esempio una velocità di primo tentativo che indicheremo con ![]() .
.
Considerando ad esempio un condotto lungo L=30m e un serbatoio alto H=6m con i rispettivi diametri di d= 0.06m e D=2m, per cui:
![]()
![]()
Per la determinazione della velocità di primo tentativo ![]() trascuriamo le perdite di carico distribuite, cioè trascuriamo il termine
trascuriamo le perdite di carico distribuite, cioè trascuriamo il termine ![]() .
.
Per cui la (3) diventa:
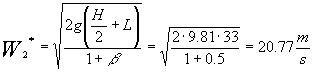 (14)
(14)
Da ciò calcoleremo il numero di Reynolds ![]() :
:
![]()
![]()
Conoscendo il numero di Reynolds e considerando il tubo "liscio" per mezzo del diagramma di "Moody" (riportato di sopra) è possibile ricavare ![]()
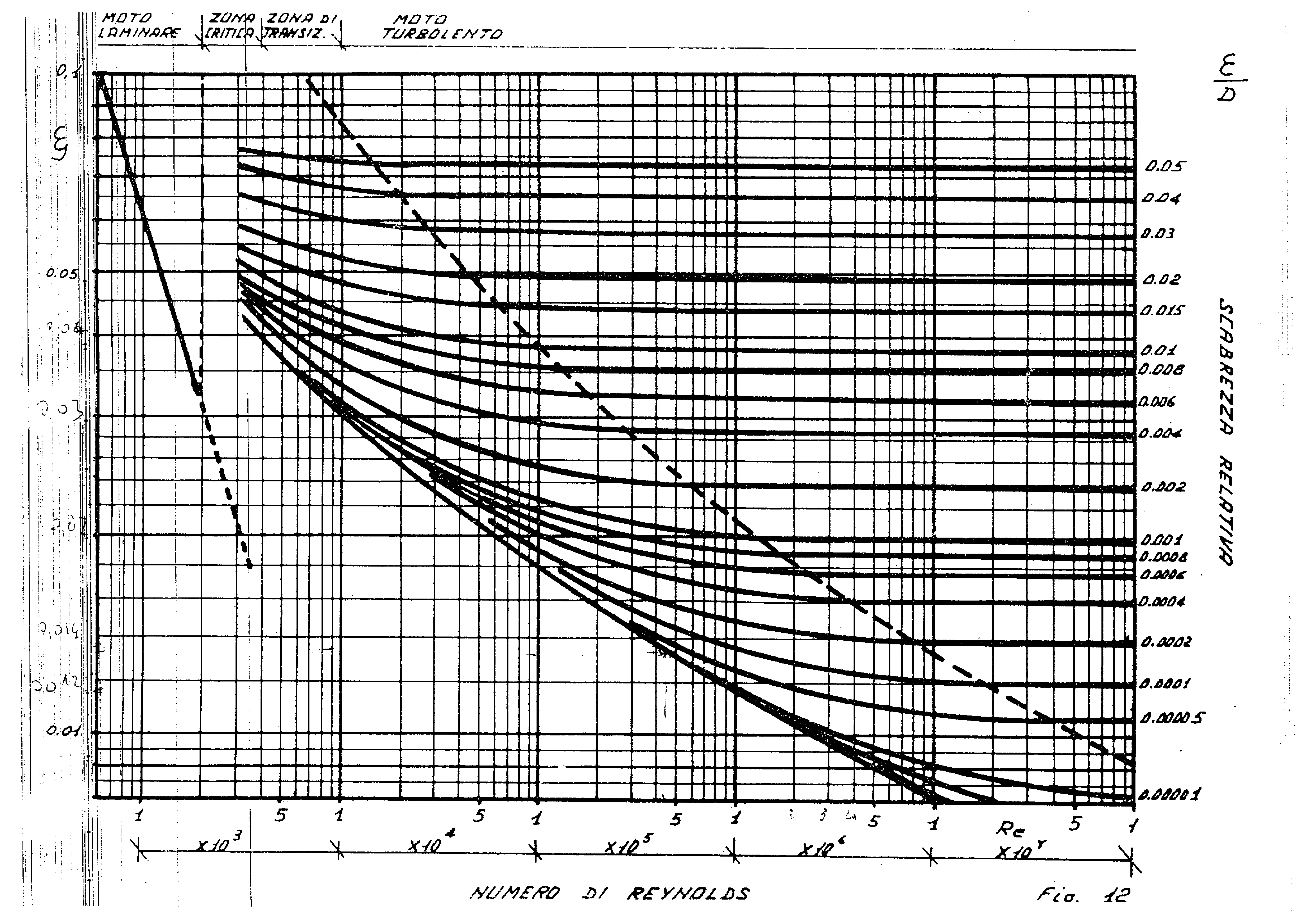
Infatti si trova :![]()
![]()
![]()
Inserendo tale valore nell’espressione (13) si ottiene:
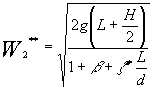 =
=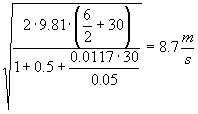 (15)
(15)
da cui :
![]()
Consultando nuovamente il diagramma di Moody, troveremo: ![]()
da cui :
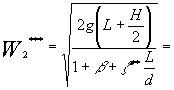
![]()
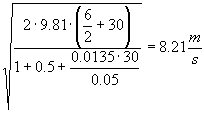
Andando avanti con le iterazioni troveremo valori di velocità sempre più vicini tra loro. Cioè:
![]() ..e cosi via..
..e cosi via..
Si osserva che lo scarto tra le due velocità è minimo (al di sotto del 5%), per cui è ragionevole considerare un valore medio di velocità: ![]()
Per calcolare il tempo necessario allo svuotamento del condotto adotteremo la formula utilizzata per l’esercizio precedente con la semplice variante di considerare in più le perdite di carico distribuite.
Per cui : 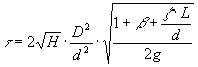
Osservazione: Avremmo potuto trovare il tempo di svuotamento come il rapporto tra il volume del serbatoio e la sua portata :
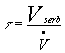 in cui :
in cui :
![]() e
e ![]()
ESERCIZIO N.3
Da un aereo è lasciata cadere una pallina (la cui forma è per semplicità approssimata con quella di una sfera) di diametro D=0.05m e massa M=1kg.
Si calcoli la velocità raggiunta dalla pallina.
Disegno:

Dati:
![]()
![]()
A tale temperatura :
![]()
![]() (viscosità cinem. dell’aria
(viscosità cinem. dell’aria![]() dato tabulato)
dato tabulato)
![]()
![]() (densità volum. dell’aria
(densità volum. dell’aria![]() dato tabulato)
dato tabulato)
Risoluzione:
Si consideri la pallina inizialmente ferma.
Quando essa è lasciata cadere verso il basso, in teoria la sua velocità dovrebbe tendere all’infinito. In realtà però, la velocità di caduta assume da un certo istante in poi un valore pressoché costante. Tutto ciò dipende strettamente dal fatto che la resistenza fluidodinamica si oppone alla forza peso. La pallina raggiungerà la sua velocità limite quando le due forze saranno esattamente bilanciate, ossia quando la resistenza dell’aria avrà eguagliato il peso della pallina.
Le due forze in questione possono essere espresse secondo le seguenti relazioni:
![]() (16)
(16)
![]() (17)
(17)
in cui:
![]() coefficiente di resistenza fluidodinamica
coefficiente di resistenza fluidodinamica
![]() area frontale
area frontale
![]() velocità di caduta
velocità di caduta
Uguagliando le due espressioni otteniamo :
![]()
![]() (18)
(18)
dalla quale ricaviamo la velocità :
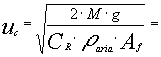
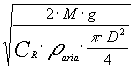 (19)
(19)
Andando a sostituire i valori :
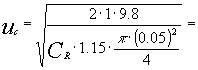
![]()
Come si può osservare abbiamo ottenuto la velocità (che è realmente la nostra incognita) in funzione del numero di Reynolds che dipende a sua volta dalla velocità! E allora??
Allora bisogna (anche qui) procedere per tentativi. Dal momento che non si ha la più pallida idea di che valore attribuire alla velocità, consideriamo un coefficiente di resistenza di primo tentativo:
![]()
Sotto tale ipotesi avremo che la velocità di primo tentativo risulta essere uguale a :
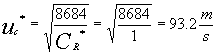 (20)
(20)
E' possibile trovare ![]() dato da :
dato da :
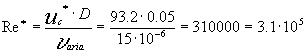
Con l’ausilio del grafico mostrato nella pagina seguente (fig 12.20 ) in cui riporteremo sull’asse delle ascisse il numero di Reynolds e su quello delle ordinate il coefficiente di resistenza valido per una superficie sferica, troveremo:
![]()
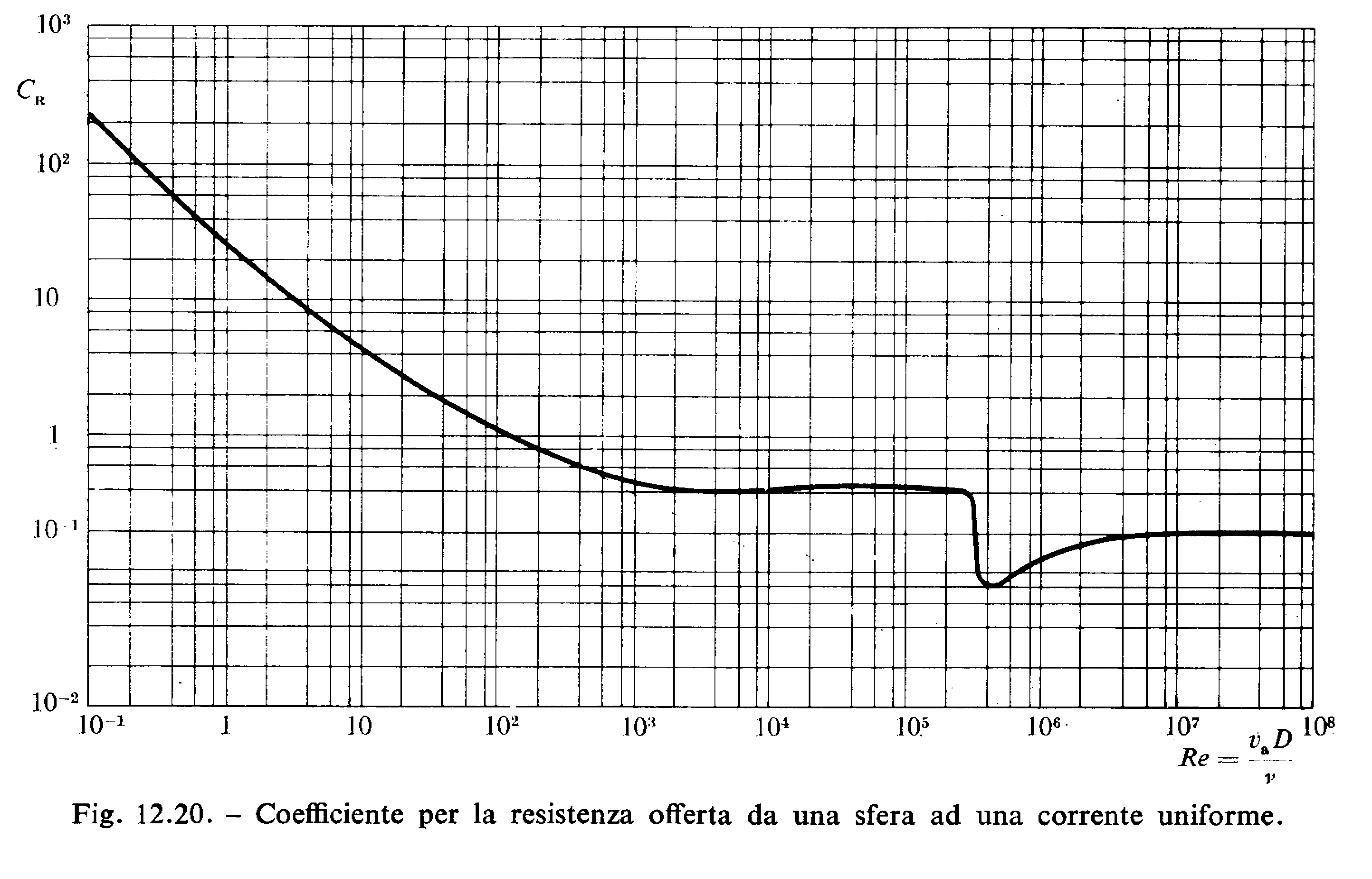
Da cui :
![]()
Notiamo di aver trovato dei valori di velocità elevati, questo perché abbiamo considerato una massa M=1kg abbastanza irragionevole (se trattasi di una pallina!).
Se ripetiamo l’esercizio con una massa ridotta pari a M=0.01kg avremo:
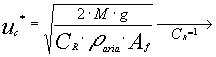
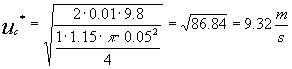
a cui corrisponde : ![]()
Osservando nuovamente il grafico (riportato di sopra) troviamo:
![]()
![]()
![]()
Facendo un ulteriore iterazione otteniamo :
![]()
![]()
![]()
![]()
![]()
Noto che lo scostamento tra ![]() e
e ![]() è nettamente inferiore al 5%. Quindi potremo fermarci con le iterazioni (anche perché nei temi d’esame è di solito ammessa una tolleranza ragionevolmente più alta per questi tipi di esercizi).
è nettamente inferiore al 5%. Quindi potremo fermarci con le iterazioni (anche perché nei temi d’esame è di solito ammessa una tolleranza ragionevolmente più alta per questi tipi di esercizi).
ESERCIZIO N.4
Determinare lo sforzo di taglio esercitato dal vento alla base del palo di una linea telefonica, supponendo che esso soffi ortogonalmente alla linea stessa.
Disegno:
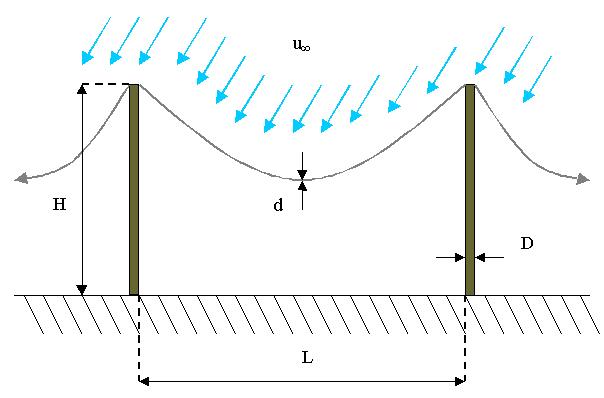
Dati:
lunghezza del cavo telefonico: ![]()
diametro del cavo telefonico: ![]()
diametro del palo di sostegno: ![]()
altezza del palo di sostegno: ![]()
temperatura dell’aria: ![]()
viscosità cinematica dell’aria (a ![]() ):
): ![]()
velocità del vento: ![]()
Risoluzione:
Lo sforzo di taglio alla base del palo è dato da due contributi :
Quindi, lo sforzo di taglio sarà uguale a:
![]() (21)
(21)
in cui:
![]() (22)
(22)
![]() (23)
(23)
Osservazione:
![]() area frontale del cavo
area frontale del cavo
![]() area frontale del palo
area frontale del palo
Sostituendo la 21) e la 22) nella 20) avremo :
![]() (24)
(24)
In questa equazione le uniche incognite sono ![]() e
e ![]() ,le quali sono espresse in funzioni del numero di Reynolds per mezzo del
,le quali sono espresse in funzioni del numero di Reynolds per mezzo del
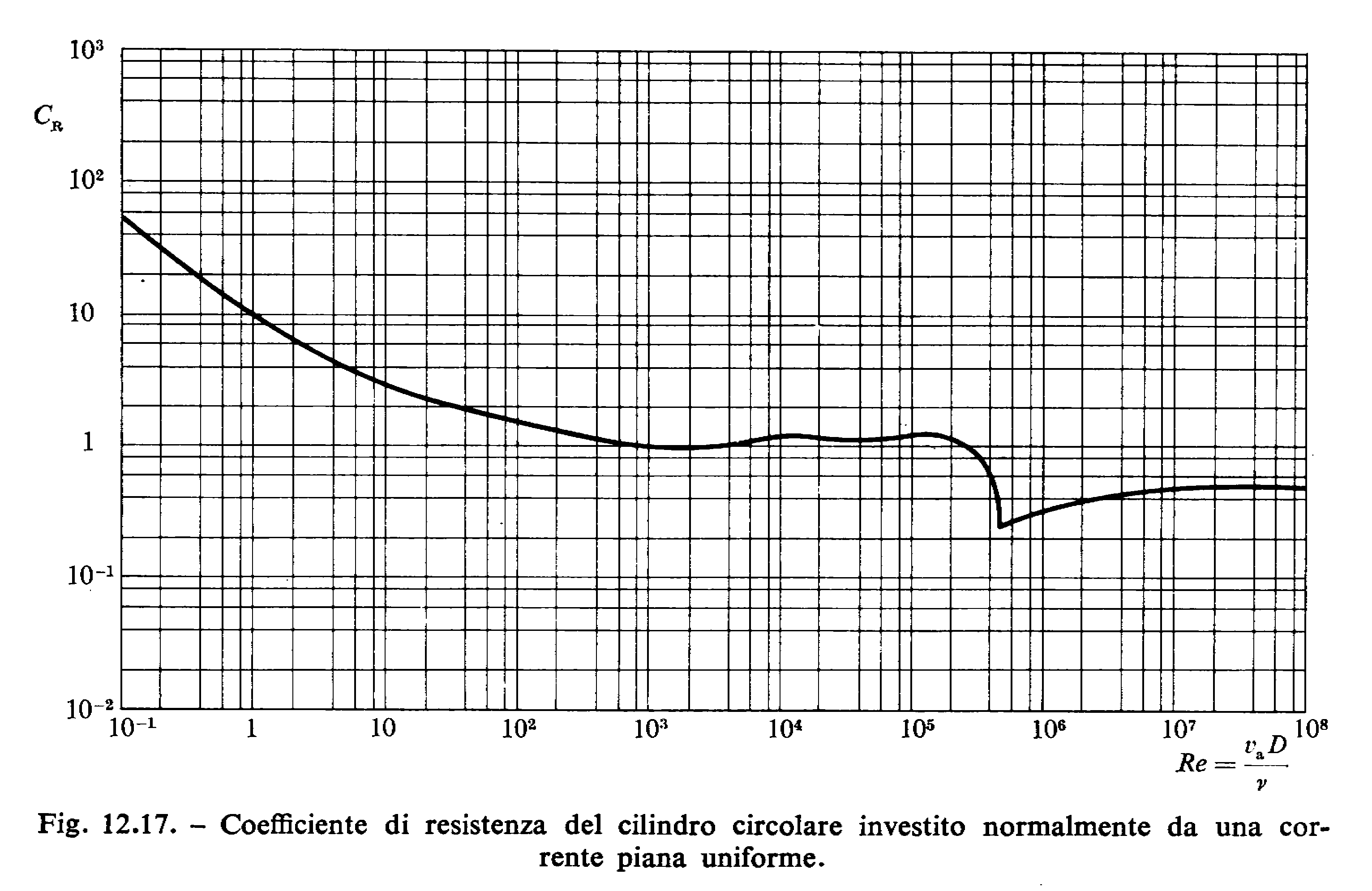
seguente grafico (fig 12.17) valido per una sup.cilindrica:
Determiniamo quindi, prima :
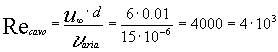
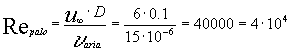
da cui con l’ausilio del grafico riportato di sopra ricaviamo :
![]()
![]()
Andando a sostituire tali valori nell’espressione (24) avremo:
![]()
Osservazione: abbiamo trovato uno sforzo alla base del palo decisamente basso. Questo perché abbiamo comunque considerato una velocità abbastanza modesta.
![]()
![]() ESERCIZIO N.5
ESERCIZIO N.5
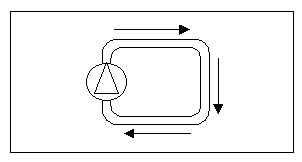
Si consideri un condotto (come in figura) alimentato da una pompa, in cui scorre dell’acqua. Calcolare :
Dati:
diametro del condotto: ![]()
lunghezza del condotto: ![]()
portata in massa dell’acqua: ![]()
Soluzione:
Questo esercizio può essere svolto in diversi modi. Il modo più semplice è quello di scegliere opportunamente le sezioni.
Considerando l’equazione del bilancio dell’energia :
![]() (25)
(25)
Può essere ad esempio una notevole semplificazione scegliere le sezioni 1 e 2 coincidenti, ma considerando la seconda dopo aver fatto un giro completo di tutto il condotto.
Sotto tale ipotesi, la (25) può essere scritta in maniera estremamente semplificata nel seguente modo:
![]() (26)
(26)
considerando il fatto che:
W1=W2 poiché siamo in regime stazionario
z1=z2 derivante dalla natura geometrica del condotto
P1=P2 poiché le sezioni coincidono
Ma chi è R?
![]() (27)
(27)
e tiene conto degli effetti dissipativi dovute alle perdite di carico concentrate e distribuite.
Osservazione:
Nell’espressione (27) appare nel secondo addendo un "4" dovuto al fatto che il condotto presenta 4 gomiti.
Esplicitiamo ora il valore della velocità del fluido. Essendo dall’equazione di continuità:
![]()
![]()
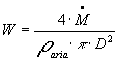
![]()
![]()
Nota la velocità, possiamo determinare il numero di Reynolds:
![]()
Consultando il diagramma di Moody (riportato nelle pagine precedenti) e considerando il tubo liscio, otteniamo:
![]()
Per cui la (27) diventa:
![]()
La prevalenza della pompa sarà quindi uguale a:
![]() (28)
(28)
ma è richiesta la prevalenza della pompa espressa in bar.
Osservando che:
![]()
Allora:
![]()
![]()
Resta da determinare la potenza della pompa:
![]()
![]() (29)
(29)
Osservazione:
Notiamo come per avere la potenza espressa in watt è necessario che la prevalenza della pompa sia espressa in ![]()
Cioè dimensionalmente:
![]()
come volevasi dimostrare.