Università degli Studi di Parma - Facoltà di Ingegneria
Corso di Laurea in Ingegneria Elettronica
Anno Accademico 2000/2001
Corso di Fisica tecnica
Prof. Angelo Farina
Lezione del 11/12/2000 Ora 14:30 ¸ 16:30
Scambio termico:
Equazione di Fourier
ed esercizi
Andrea Toscani Matricola 103754
Indice
Come già visto per l’acustica, in cui partendo dalla legge di Eulero si costruisce l’equazione di D’Alambert, e per il moto dei fluidi in cui dalla legge di Newton si ricava l’equazione di Navier, anche per la trasmissione del calore dalla legge di Fourier è possibile ricavare una equazione differenziale di secondo ordine che descrive la dinamica del fenomeno. La differenza sostanziale è che, mentre per i primi due casi citati il passaggio dalla legge costitutiva all’equazione differenziale rappresenta solo un’operazione matematica fine a se stessa, per lo scambio termico l’equazione di Fourier, ricavata dall’omonima legge, è un utile strumento per risolvere, mediante una integrazione numerica dell’equazione, alcuni casi pratici di transitori termici.
Per ricavare l’equazione di Fourier occorre considerare un elemento infinitesimo di volume![]() nel campo scalare delle temperature, e scrivere l’equazione di bilancio dell’energia applicando il primo principio della termodinamica.
nel campo scalare delle temperature, e scrivere l’equazione di bilancio dell’energia applicando il primo principio della termodinamica.
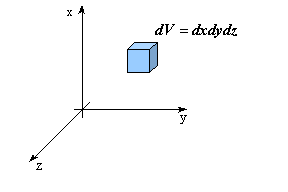
L’energia interna del volume infinitesimo ![]() (considerato rigido e indeformabile, motivo per il quale si usa il calore specifico a volume costante
(considerato rigido e indeformabile, motivo per il quale si usa il calore specifico a volume costante ![]() ) è data dall’espressione:
) è data dall’espressione:
![]() (1.1)
(1.1)
avendo assunto il volume infinitesimo indeformabile esso non può compiere nessun lavoro, percui la sua variazione di energia interna è uguale al flusso infinitesimo di energia entrante:
![]() (1.2)
(1.2)
il termine ![]() viene espresso come il differenziale dell’espressione (1.1)
viene espresso come il differenziale dell’espressione (1.1)
![]() (1.3)
(1.3)
mentre per calcolare l’espressione di ![]() è necessario tenere conto di due distinti contributi: il calore scambiato attraverso l’intera superficie esterna del volume
è necessario tenere conto di due distinti contributi: il calore scambiato attraverso l’intera superficie esterna del volume ![]() e il calore generato all’interno del volume stesso (si pensi, per esempio, ad un conduttore percorso da corrente elettrica che genera per effetto Joule una certa quantità di calore per unità di volume, oppure ad un corpo che partecipa ad una reazione chimica o nucleare). Risulta quindi:
e il calore generato all’interno del volume stesso (si pensi, per esempio, ad un conduttore percorso da corrente elettrica che genera per effetto Joule una certa quantità di calore per unità di volume, oppure ad un corpo che partecipa ad una reazione chimica o nucleare). Risulta quindi:
![]() (1.4)
(1.4)
dove: ![]() è il calore scambiato e
è il calore scambiato e ![]() è il calore generato internamente.
è il calore generato internamente.
Il termine ![]() a sua volta si esprime come il prodotto del termine
a sua volta si esprime come il prodotto del termine ![]() (quantità di calore generato per unità di tempo e unità volume, dimensionalmente [W/m3]), moltiplicato per
(quantità di calore generato per unità di tempo e unità volume, dimensionalmente [W/m3]), moltiplicato per ![]() e
e ![]() :
:
![]() (1.5)
(1.5)
(Nota: per calcolare ![]() si fa riferimento ad un infinitesimo di volume e non di massa perché esistono dei fenomeni generativi che sono proporzionali al volume e non al "peso" del sistema: si pensi, per fare un esempio eclatante, alle reazioni nucleari che interessano particelle di massa infinitesimale percui facendo riferimento a infinitesimi di massa si perderebbe ogni significato fisico).
si fa riferimento ad un infinitesimo di volume e non di massa perché esistono dei fenomeni generativi che sono proporzionali al volume e non al "peso" del sistema: si pensi, per fare un esempio eclatante, alle reazioni nucleari che interessano particelle di massa infinitesimale percui facendo riferimento a infinitesimi di massa si perderebbe ogni significato fisico).
Il termine ![]() si ottiene integrando sulla superficie esterna
si ottiene integrando sulla superficie esterna ![]() del volume
del volume ![]() il flusso di calore (l’integrazione su una superficie infinitesima
il flusso di calore (l’integrazione su una superficie infinitesima ![]() può sembrare una "forzatura" matematica, ma permetterà in seguito di applicare il teorema di Gauss)
può sembrare una "forzatura" matematica, ma permetterà in seguito di applicare il teorema di Gauss)
![]() (1.6)
(1.6)
dove ![]() è il versore orientato verso l’esterno e ortogonale alle facce dell’elemento di volume, percui il termine
è il versore orientato verso l’esterno e ortogonale alle facce dell’elemento di volume, percui il termine ![]() rappresenta la componente di
rappresenta la componente di ![]() parallela al versore
parallela al versore ![]() . Il segno meno davanti all’integrale si giustifica con le convenzioni termodinamiche sul calore scambiato.
. Il segno meno davanti all’integrale si giustifica con le convenzioni termodinamiche sul calore scambiato.
Applicando il teorema di Gauss, si trasforma l’integrale di superficie in un integrale di volume, e l’espressione diventa
![]() (1.7)
(1.7)
Ora, considerando che l’integrazione avviene su un elemento di volume infinitesimo ![]() il simbolo di integrale si può depennare senza alterare il significato fisico dell’espressione, percui
il simbolo di integrale si può depennare senza alterare il significato fisico dell’espressione, percui
![]() (1.8)
(1.8)
ricordando poi che, per la legge di Fourier,
![]() (1.9)
(1.9)
si ottiene
![]() (1.10)
(1.10)
considerando la conducibilità termica ![]() costante (questa ipotesi verrà discussa meglio in seguito) si può portarla fuori dall’operatore divergenza e scrivere:
costante (questa ipotesi verrà discussa meglio in seguito) si può portarla fuori dall’operatore divergenza e scrivere:
![]() (1.11)
(1.11)
ricordando che:![]() si ricava infine
si ricava infine
![]() (1.12)
(1.12)
sostituendo nella relazione (1.2) che esprime il bilancio di energia per il volume infinitesimo considerato le espressioni (1.3), (1.5) e (1.12) si ricava
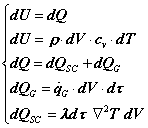 Þ
Þ
Þ
![]() (1.13)
(1.13)
semplificando per il termine ![]() che compare in ambo i membri e dividendo per l’infinitesimo
che compare in ambo i membri e dividendo per l’infinitesimo ![]() e per
e per ![]() si ottiene
si ottiene
![]() (1.14)
(1.14)
(nota: la derivata della temperatura ![]() rispetto al tempo
rispetto al tempo ![]() si scrive col simbolo di derivata parziale per sottolineare che la temperatura dipende anche dalle coordinate spaziali).
si scrive col simbolo di derivata parziale per sottolineare che la temperatura dipende anche dalle coordinate spaziali).
L’espressione (1.14) prende il nome di equazione di Fourier, e permette di ricavare l’andamento della temperatura ![]() una volta assegnate le opportune condizioni al contorno.
una volta assegnate le opportune condizioni al contorno.
L’equazione di Fourier governa la variazione della temperatura nel tempo in funzione del gradiente spaziale, quindi indica quanto varierà la temperatura nel tempo a causa o degli effetti generativi o degli effetti di trasporto del calore. L’equazione di Fourier, al contrario della legge di Fourier che permette di studiare i soli fenomeni termici stazionari, consente dunque di studiare i transitori termici.
L’importanza dello studio dei transitori termici è evidente: si consideri per esempio un diodo che sia utilizzato come raddrizzatore a singola semionda, esso deve dissipare energia solo quando è polarizzato direttamente, cioè per il 50% del tempo. Il regime termico al quale è sottoposto è quindi periodico, cioè composto da una serie di transitori termici che si susseguono regolarmente nel tempo. Il termine di generazione interna appare e scompare con regolarità periodica. Lo studio di un fenomeno del genere (considerando la frequenza di rete di 50 Hz) utilizzando un regime non transitorio equivalente sarebbe scorretto e porterebbe a conclusioni errate.
Si consideri una lastra piana di spessore ![]() ad una temperatura uniforme
ad una temperatura uniforme ![]() che viene immersa in un fluido a temperatura
che viene immersa in un fluido a temperatura![]() . Appena la lastra viene messa a contatto con il fluido inizia uno scambio di calore: all’inizio solo un sottile strato esterno della lastra "sente" che la temperatura esterna è cresciuta e si adegua. Trascorso un tempo un po’ maggiore la temperatura esterna inizia a far crescere la temperatura della lastra fino ad una certa profondità dalla superficie, mentre il nocciolo della lastra non ha ancora subito nessuna variazione di temperatura. Al trascorrere del tempo la variazione di temperatura della lastra a causa del fluido penetra sempre più in profondità, fino ad influenzare anche la parte più interna. Asintoticamente si tende a raggiungere in tutta la lastra un temperatura uniforme
. Appena la lastra viene messa a contatto con il fluido inizia uno scambio di calore: all’inizio solo un sottile strato esterno della lastra "sente" che la temperatura esterna è cresciuta e si adegua. Trascorso un tempo un po’ maggiore la temperatura esterna inizia a far crescere la temperatura della lastra fino ad una certa profondità dalla superficie, mentre il nocciolo della lastra non ha ancora subito nessuna variazione di temperatura. Al trascorrere del tempo la variazione di temperatura della lastra a causa del fluido penetra sempre più in profondità, fino ad influenzare anche la parte più interna. Asintoticamente si tende a raggiungere in tutta la lastra un temperatura uniforme![]() .
.
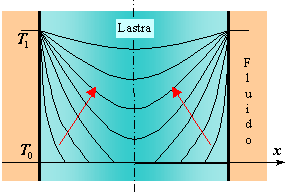
Fissato ![]() ecco come varia la temperatura
ecco come varia la temperatura ![]() con il tempo:
con il tempo:
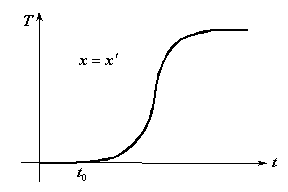
Il ritardo ![]() con cui la temperatura nel punto con ascissa
con cui la temperatura nel punto con ascissa ![]() inizia ad adeguarsi all’avvenuto cambiamento denuncia chiaramente la presenza di un ritardo nella propagazione del calore (come conferma anche l’esperienza pratica di tutti i giorni): in altre parole si vede chiaramente che la trasmissione del calore non avviene a velocità infinita. L’equazione di Fourier, essendo priva di un termine non omogeneo che corrisponde ad una velocità finita di propagazione (si confronti con l’equazione dell’acustica in cui compare espressamente un termine la velocità del suono
inizia ad adeguarsi all’avvenuto cambiamento denuncia chiaramente la presenza di un ritardo nella propagazione del calore (come conferma anche l’esperienza pratica di tutti i giorni): in altre parole si vede chiaramente che la trasmissione del calore non avviene a velocità infinita. L’equazione di Fourier, essendo priva di un termine non omogeneo che corrisponde ad una velocità finita di propagazione (si confronti con l’equazione dell’acustica in cui compare espressamente un termine la velocità del suono ![]() ), invece prevede una propagazione istantanea del calore.
), invece prevede una propagazione istantanea del calore.
Tutto ciò significa che la soluzione matematica che si ricava dall’equazione di Fourier non corrisponde esattamente alla realtà fisica del fenomeno: il modello semplificato usato per rappresentare il fenomeno non è sufficientemente accurato. La correzione di questa discrepanza comporterebbe notevoli complicazioni matematiche, percui si preferisce risolvere l’equazione di Fourier con metodi numerici.
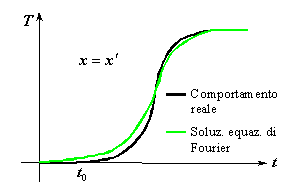
La soluzione numerica dell’equazione di Fourier si realizza discretizzando la geometria del sistema e discretizzando l’asse temporale. Questa tecnica introduce artificiosamente una velocità di propagazione finita poiché all’i-esimo passo temporale solo il j-esimo nodo ha informazioni riguardo alle variazioni che hanno riguardato il nodo precedente, e solo al passo i+1 il nodo successivo (j+1) conoscerà quello che è successo al suo predecessore. La scelta di un congruo passo spaziale a fronte della scelta di un congruo passo temporale introduce un limite alla velocità massima di propagazione. In sostanza la soluzione numerica trovata approssima abbastanza bene il risultato sperimentale, compensando inaspettatamente le lacune del modello analitico. La soluzione numerica, con una opportuna calibrazione del passo temporale e del passo spaziale, invece di aggiungere errori ed errori come ci si sarebbe potuti aspettare, migliora le cose.
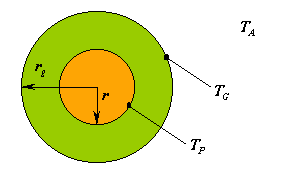
Si consideri un conduttore elettrico cilindrico di sezione ![]() e lunghezza
e lunghezza ![]() . Il cavo è percorso da corrente percui viene generato al suo interno calore per effetto Joule, tale calore viene disperso nell’ambiente circostante per irraggiamento e convezione con coefficiente di adduzione
. Il cavo è percorso da corrente percui viene generato al suo interno calore per effetto Joule, tale calore viene disperso nell’ambiente circostante per irraggiamento e convezione con coefficiente di adduzione ![]() . Il conduttore è percorso da una corrente
. Il conduttore è percorso da una corrente ![]() e ha una resistenza per unità di lunghezza di
e ha una resistenza per unità di lunghezza di ![]() (si tratta di un conduttore di pessima qualità). Determinare la temperatura
(si tratta di un conduttore di pessima qualità). Determinare la temperatura ![]() della parete esterna del conduttore nel caso in cui la temperatura esterna sia
della parete esterna del conduttore nel caso in cui la temperatura esterna sia ![]() .
.
La potenza dispersa a causa di irraggiamento e convezione è data dalla formula
![]() (3.1)
(3.1)
dove ![]() è la superficie laterale del conduttore cilindrico (fig. 3.1).
è la superficie laterale del conduttore cilindrico (fig. 3.1).
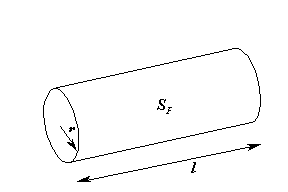
La potenza termica dissipata per effetto Joule sull’intero conduttore vale
![]() (3.2)
(3.2)
Il raggio del conduttore è dato dalla relazione
![]() (3.3)
(3.3)
percui la superficie laterale del conduttore (attraverso la quale si sviluppa il flusso termico) risulta
![]() (3.4)
(3.4)
Ora risulta immediato il calcolo della temperatura di parete, ricavando ![]() dalla relazione (3.1) si ottiene
dalla relazione (3.1) si ottiene
![]() (3.5)
(3.5)
La temperatura di parete risulta molto elevata, nonostante il rame la possa sopportare, essa rappresenta un pericolo per le persone che ne entrassero inavvertitamente in contatto.
È quindi consigliabile ricoprire il conduttore con una guaina isolante di gomma di raggio ![]() . La conducibilità termica della gomma utilizzata vale
. La conducibilità termica della gomma utilizzata vale ![]() .
.
Il raggio ottimale della guaina è dato dalla formula che esprime il raggio critico
![]() (3.6)
(3.6)
si sceglie dunque ![]() in modo da massimizzare lo scambio termico del conduttore con l’ambiente (fig. 3.3).
in modo da massimizzare lo scambio termico del conduttore con l’ambiente (fig. 3.3).
La potenza termica scambiata, nella nuova condizione risulta:
![]() (3.7)
(3.7)
dove ![]() è la resistenza termica totale che incontra in flusso termico, composta da due contributi, uno dovuto alla resistenza termica dello strato cilindrico di guaina
è la resistenza termica totale che incontra in flusso termico, composta da due contributi, uno dovuto alla resistenza termica dello strato cilindrico di guaina ![]() e uno alla resistenza di convezione/irraggiamento
e uno alla resistenza di convezione/irraggiamento ![]()
![]() (3.8)
(3.8)
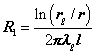 (3.9)
(3.9)
![]() (3.10)
(3.10)
sostituendo le espressioni (3.9) e (3.10) nella relazione (3.7), si ottiene
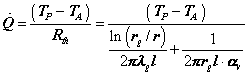 (3.11)
(3.11)
Ricavando dalla (3.11) l’espressione della temperatura della parete esterna del conduttore di rame ![]() si ottiene
si ottiene
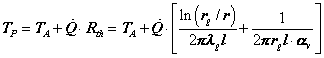 (3.12)
(3.12)
sostituendo i valori numerici
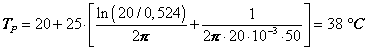 (3.13)
(3.13)
La temperatura della superficie del conduttore di rame è ora ad una temperatura più che accettabile. In questo caso però l’analogia elettrica non riesce a spiegare la diminuzione della temperatura della parete. A rigor di logica, aggiungendo una ulteriore resistenza, la temperatura sarebbe dovuta crescere anziché calare. Il fatto è che la guaina ha aumentato di molto la superficie di scambio e quindi ha favorito una diminuzione della temperatura di parete.
Un altro parametro da valutare è la temperatura della parete esterna dell’isolante ![]() , per il calcolo è utile ricordare l’analogia elettrica ed applicare la formula del partitore di tensione:
, per il calcolo è utile ricordare l’analogia elettrica ed applicare la formula del partitore di tensione:
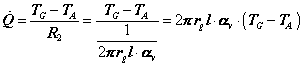 (3.14)
(3.14)
ricavando ![]() si ha
si ha
![]() (3.15)
(3.15)
sostituendo i valori numerici:
![]()
Si consideri un conduttore elettrico di acciaio inox percorso da corrente elettrica con conducibilità termica ![]() e raggio
e raggio ![]() . L’obiettivo è di calcolare l’andamento della temperatura in funzione del raggio
. L’obiettivo è di calcolare l’andamento della temperatura in funzione del raggio ![]() .
.
Per la soluzione si hanno due possibilità: la prima consiste nello scrivere l’equazione di Fourier per una geometria cilindrica, aggiungere il termine generativo e risolverla. La seconda possibilità consiste nello sfruttare la legge di Fourier ripetendo i ragionamenti fatti per ricavare l’equazione di Fourier ma prendendo come volume infinitesimo una corona cilindrica. Quest’ultima possibilità risulta preferibile.
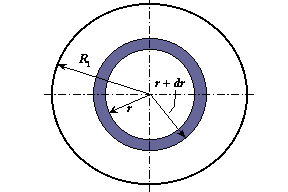
Il bilancio di energia per la corona è:
![]() (4.1)
(4.1)
cioè
![]() (4.2)
(4.2)
ma
![]() (4.3)
(4.3)
![]() (4.4)
(4.4)
![]() (4.5)
(4.5)
sostituendo le relazioni (4.3), (4.4) e (4.5) nell’equazione (4.2) si ricava
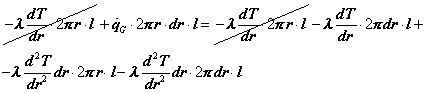 (4.6)
(4.6)
l’ultimo termine di questa espressione è un infinitesimo del secondo ordine ed è trascurabile, inoltre è possibile semplificare per ![]() che è presente in tutti i termini, e dividere per
che è presente in tutti i termini, e dividere per![]() , si ha allora
, si ha allora
![]() (4.7)
(4.7)
Risolvendo questa equazione differenziale del secondo ordine, ed imponendo le condizioni al contorno, si ricava la funzione ![]() cercata.
cercata.
La conduttività termica ![]() in generale ha una certa dipendenza dalla temperatura e in alcuni casi si riscontrano forti variazioni, tali da indurre scostamenti notevoli dalle distribuzioni di temperatura ricavate nell’ipotesi di conduttività termica costante.
in generale ha una certa dipendenza dalla temperatura e in alcuni casi si riscontrano forti variazioni, tali da indurre scostamenti notevoli dalle distribuzioni di temperatura ricavate nell’ipotesi di conduttività termica costante.
Nel caso di conduttività termica funzione della temperatura ![]() , l’equazione di Fourier si scrive nella forma:
, l’equazione di Fourier si scrive nella forma:
![]() (5.1)
(5.1)
supponendo nullo il termine di generazione, cioè ![]() , considerando un regime stazionario, cioè
, considerando un regime stazionario, cioè ![]() , e scrivendo l’equazione per una geometria monodimensionale si ottiene
, e scrivendo l’equazione per una geometria monodimensionale si ottiene
![]() (5.2)
(5.2)
Si applichi la relazione (5.2) al caso di una lastra piana di spessore ![]() , e siano date le seguenti condizioni al contorno:
, e siano date le seguenti condizioni al contorno:
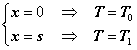 (5.3)
(5.3)
Si supponga che ![]() , sostituendo nell’equazione (5.2) si ottiene
, sostituendo nell’equazione (5.2) si ottiene
![]() (5.4)
(5.4)
che equivale, grazie alla linearità dell’operatore derivata, a
![]() (5.5)
(5.5)
Integrando l’espressione (5.5) si individua una prima costante ![]()
![]() (5.6)
(5.6)
integrando una seconda volta
![]() (5.7)
(5.7)
si individua anche la seconda costante ![]() .
.
Ora bisogna imporre le condizioni al contorno nella (5.6) per ricavare l’espressione analitica delle due costanti ![]() e
e ![]()
![]() si ha
si ha ![]()
![]() si ha
si ha ![]()
cioè 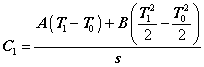
Riassumendo si è ottenuto
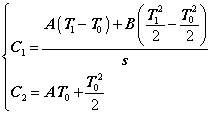 (5.8)
(5.8)
sostituendo le espressioni delle costanti così ottenute nella (5.7) si ricava l’andamento di ![]()
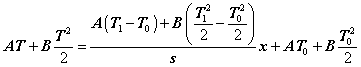 (5.9)
(5.9)
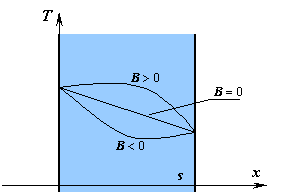
L’equazione (5.9) rappresenta, sul piano (![]() ) una parabola ad asse orizzontale. La concavità della parabola è determinata dal segno del coefficiente
) una parabola ad asse orizzontale. La concavità della parabola è determinata dal segno del coefficiente ![]() :
:
|
Segno di |
Significato fisico |
Verso della concavità |
|
|
La conduttività aumenta con l’aumento di |
Concavità verso sinistra |
|
|
La conduttività è costante al variare di |
(andamento rettilineo) |
|
|
La conduttività cala con l’aumento di |
Concavità verso destra |
Graficamente le situazione è la seguente
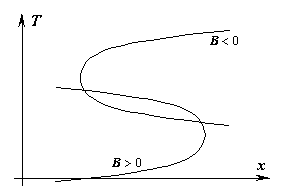
La gran parte dei materiali presenta una conducibilità termica che cresce con la temperatura, cioè ![]() , e questo porta normalmente ad uno scambio termico più elevato rispetto a quello che si avrebbe con una conducibilità termica costante (
, e questo porta normalmente ad uno scambio termico più elevato rispetto a quello che si avrebbe con una conducibilità termica costante (![]() ). Questo comportamento è gradito, per esempio, nel caso in cui si abbia da raffreddare un componente elettronico. Nonostante ciò comunque, siccome i dimensionamenti di questo genere si fanno sempre in maniera "prudente", nei calcoli non si considera la variabilità di
). Questo comportamento è gradito, per esempio, nel caso in cui si abbia da raffreddare un componente elettronico. Nonostante ciò comunque, siccome i dimensionamenti di questo genere si fanno sempre in maniera "prudente", nei calcoli non si considera la variabilità di ![]() proprio perché trascurarla garantisce un ulteriore margine di sicurezza.
proprio perché trascurarla garantisce un ulteriore margine di sicurezza.
Nel caso in cui, viceversa, si debba realizzare un isolamento termico, per esempio di un edificio, la variabilità di ![]() , che aumenta lo scambio termico complessivo, è un comportamento deleterio, ragione per cui si correggono i calcoli sviluppati comunque con conducibilità termica costante attraverso un opportuno coefficiente di sicurezza.
, che aumenta lo scambio termico complessivo, è un comportamento deleterio, ragione per cui si correggono i calcoli sviluppati comunque con conducibilità termica costante attraverso un opportuno coefficiente di sicurezza.
Una ulteriore considerazione si può fare riprendendo la legge di Fourier
![]() (5.10)
(5.10)
Poiché in condizioni stazionarie ![]() rimane ovunque costante, si può affermare che nella zona della lastra in cui la temperatura
rimane ovunque costante, si può affermare che nella zona della lastra in cui la temperatura ![]() è più elevata, la conducibilità termica
è più elevata, la conducibilità termica ![]() è più elevata, il gradiente è più piccolo e quindi la pendenza è minore. Nella zona in cui
è più elevata, il gradiente è più piccolo e quindi la pendenza è minore. Nella zona in cui ![]() è minore, seguendo lo stesso schema di ragionamento, si conclude che la pendenza è maggiore.
è minore, seguendo lo stesso schema di ragionamento, si conclude che la pendenza è maggiore.