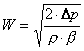Spaggiari
Emanuele matr-127243 lezione del 06/11/00
Richiamo dell’ equazione di Navier
Nella
lezione precedente eravamo arrivati all’equazione di Navier scritta in
regime
non
stazionario
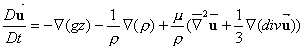
dove
sappiamo che se trascuriamo l’ ultimo termine diventa :
![]()
che
è l’equazione di Navier per un fluido incomprimibile nel quale non vi è
variazione di massa nel volumetto (figura 1) di fluido considerato durante
l’intervallo infinitesimo dt.
![]()
Consideriamo un elemento di volume
infinitesimo su cui agiscono forze viscose lungo l’asse y.
In figura sono indicate la direzione di queste forze.
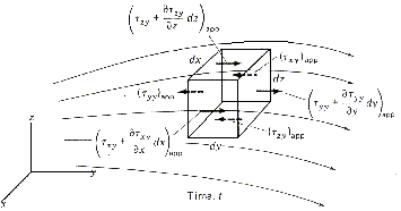
Figura 1:Rappresentazione delle forze viscose in un elemento infinitesimo.
Quindi
la somma di tutti questi sforzi lungo l’asse y mi da la forza viscosa lungo
l’asse y e cioè:
![]()
Considerando
anche le componenti x e y e servendoci dei versori avremo che :
![]()
da
cui :
![]()
Se
il fluido è incomprimibile ed è Newtoniano si hanno le seguenti definizioni
generali di viscosità :
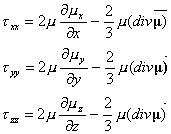
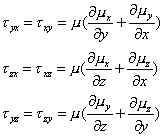
![]()
Combinando queste equazioni arriviamo all’
equazione di Navier scritta in regime non stazionario.
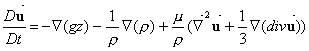
![]()
Esercizio sulle perdite di carico.
![]()
Si
abbia un condotto di sezione rettangolare nel quale scorre aria avente una
pressione PARIA= 1 atm. Determinare le perdite di carico Δp
lungo il condotto, considerando in un primo caso una temperatura dell’ aria T1
= 25 ˚C, e in un secondo una T2 = 80
˚C.
Del
condotto si conoscono le dimensioni :
B
= 0.70 m
H
= 0.25 m
L
= 25.0 m
e la portata in volume dell’aria del
condotto
![]()
Soluzione :
Sapendo
che la formula per il calcolo delle perdite di carico è :
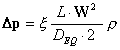
Dove ρ è la densità dell’ acqua, ξ
è il fattore di attrito , W è la velocità dell’ aria nel condotto (ed è l’
unica incognita che ci manca per risolvere il nostro problema!), DEQ
Cioè il DEQ è quel valore dato dalla formula
![]()
è il diametro equivalente .
che
devo utilizzare tutte le volte che ho a che fare con sezioni non circolari,
dove A è la sezione del condotto e PBAGNATO è il perimetro bagnato dal fluido.
● Calcoliamo il DEQ :
![]()
● Calcoliamo la
velocità del fluido W (velocità media):
Dalla
definizione di portata abbiamo:
![]()
da cui :
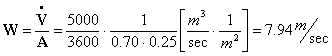
dalla tabella per una T1 = 25°C otteniamo i seguenti risultati:
![]()
Tab.1 – Caratteristiche dell’ aria secca alla pressione di 1 atm.
|
Temperatura |
Densità |
Calore specifico |
Viscosità dinamica |
Viscosità cinematica |
|||
|
t |
T |
ρ |
cp |
μ·10-6 |
ν·10-6 |
||
|
°C |
K |
Kg/m3 |
Kcal/KgK |
KJ/KgK |
Kgfs/m2 |
Ns/m2 |
m2/s |
|
-180 |
93.15 |
3.720 |
0.2500 |
1.047 |
0.660 |
6.472 |
1.75 |
|
-150 |
123.15 |
2.780 |
0.2480 |
1.037 |
0.876 |
8.591 |
3.14 |
|
-100 |
173.15 |
1.948 |
0.2440 |
1.022 |
1.210 |
11.866 |
5.96 |
|
-50 |
223.15 |
1.534 |
0.2420 |
1.013 |
1.510 |
14.808 |
9.65 |
|
-20 |
253.15 |
1.365 |
0.2400 |
1.005 |
1.660 |
16.279 |
12.00 |
|
0 |
273.15 |
1.252 |
0.2414 |
1.011 |
1.780 |
17.456 |
13.90 |
|
10 |
283.15 |
1.206 |
0.2415 |
1.010 |
1.820 |
17.848 |
14.66 |
|
20 |
293.15 |
1.164 |
0.2416 |
1.012 |
1.860 |
18.240 |
15.70 |
|
30 |
303.15 |
1.127 |
0.2419 |
1.013 |
1.905 |
18.682 |
16.58 |
|
40 |
313.15 |
1.092 |
0.2422 |
1.014 |
1.950 |
19.123 |
17.60 |
|
50 |
323.15 |
1.057 |
0.2426 |
1.016 |
1.990 |
19.515 |
18.58 |
|
60 |
333.15 |
1.025 |
0.2429 |
1.017 |
2.030 |
19.907 |
19.40 |
|
70 |
343.15 |
0.996 |
0.2432 |
1.018 |
2.080 |
20.398 |
20.65 |
|
80 |
353.15 |
0.968 |
0.2435 |
1.019 |
2.120 |
20.790 |
21.50 |
|
90 |
363.15 |
0.942 |
0.2438 |
1.021 |
2.165 |
21.231 |
22.82 |
|
100 |
373.15 |
0.916 |
0.2441 |
1.022 |
2.210 |
21.673 |
23.60 |
|
120 |
393.15 |
0.870 |
0.2447 |
1.025 |
2.300 |
22.555 |
25.90 |
|
140 |
413.15 |
0.827 |
0.2453 |
1.027 |
2.380 |
23.340 |
28.20 |
|
150 |
423.15 |
0.810 |
0.2456 |
1.028 |
2.420 |
23.732 |
29.40 |
|
160 |
433.15 |
0.789 |
0.2460 |
1.030 |
2.460 |
24.124 |
30.60 |
|
180 |
453.15 |
0.755 |
0.2466 |
1.032 |
2.540 |
24.909 |
33.00 |
|
200 |
473.15 |
0.723 |
0.2472 |
1.025 |
2.620 |
25.693 |
35.50 |
|
250 |
523.15 |
0.653 |
0.2490 |
1.043 |
2.810 |
27.557 |
42.20 |
|
300 |
573.15 |
0.596 |
0.2500 |
1.047 |
2.990 |
29.322 |
49.20 |
![]()
![]()
Dobbiamo calcolare il numero di Reynolds per calcolare se il regime è laminare o turbolento:
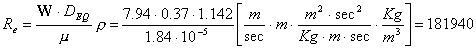
Cioè
abbiamo che il regime è turbolento.
Dal
diagramma di Moody calcoliamo il valore
di ξ , per fare questo mi manca la scabrezza relativa.In questo caso
consideriamo il tubo liscio e otteniamo uno
ξ= 0.016.
![]()
A questo punto abbiamo tutto per calcolarci
la caduta di pressione dovuta alle perdite distribuite quindi abbiamo che :
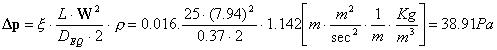
Consideriamo
ora il caso di una temperatura T2 di 80 ˚C ;
le caratteristiche dell’ aria sono:
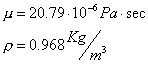
La velocità è ancora uguale, mentre il numero
di Reynolds è :
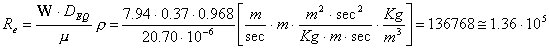
Quindi
dal diagramma di Moody ricaviamo uno ξ=0.0175 e quindi :
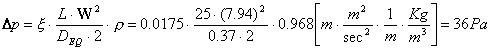
Quindi abbiamo che la caduta di pressione è diminuita ed è passata da 38 a 36 Pa a seguito di un aumento di temperatura di 55 ˚C.
Strumenti di misura
Gli
strumenti di misura della fluidodinamica si possono sostanzialmente dividere in
due tipi :
● Strumenti per misurare la velocità media (o
portata ) di un fluido.
● Strumenti per misurare la velocità locale
di un fluido.
Il metodo della pesata
E’ il metodo più semplice che mi permette di determinare la portata di un fluido, e quindi la sua velocità media (appartiene al primo tipo di strumento) .
Il funzionamento è dato da un recipiente graduato in cui finisce il fluido di cui si vuole misurare la velocità.Conoscendo la quantità di liquido che riempie il recipiente in un dato periodo di tempo siamo in grado di calcolarci la portata in massa tramite la formula elementare :
![]()
Questo metodo, ha grossi limiti dal punto di vista della precisione, infatti non è per niente facile sincronizzare l’inizio del tempo della misura con l’arrivo del liquido nel recipiente.
Infatti si capisce che al tempo iniziale T=0 a cui corrisponde l’apertura della valvola il flusso dell’ acqua non arriverà subito a “regime”, ma ci sarà un “transitorio” di tempo in cui il flusso del liquido uscirà più piano.
Tubo di Pitot
Strumento di misura della velocità locale in un fluido in moto.
Il tubo di Pitot si basa sulla considerazione sperimentalmente effettuata da H.Pitot (1732) che , immergendo in una corrente liquida un tubo, piegato ad angolo retto, aperto da ambedue le estremità, una delle quali rivolta controcorrente,il liquido sale in esso al di sopra del livello statico di una altezza proporzionale all’ altezza cinetica
W2/2g , ove W è la velocità del fluido nel punto considerato e g è la accelerazione di gravità.
H. Darcy unì due tubi uno rivolto contro corrente e l’ altro in senso opposto .
Il dislivello tra i due menischi (peli liberi nei due tubi) è ancora proporzionale all’altezza cinetica e la velocità può essere calcolata mediante la formula :
![]()
ove con h1 –h2 si è indicato il dislivello tra i due menischi e con K un coefficiente di velocità che dipende dalla forma dell’ estremità, dal tipo di fluido e dalle condizioni di moto.
I tubi di Pitot che attualmente si usano attualmente sono due : il tipo Prandtl, che ha l’estremità semisferica (fig. 2a), ed il tipo Brabbè, che ha l’ estremità tronco conica (fig. 2b).
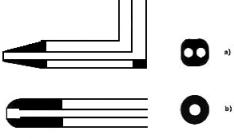
Figura 2: Tubo di Brabbè (a) e di Prandtl (b) , sezioni laterali
Entrambi i tipi sono formati da due tubi coassiali.Il tubo esterno presenta dei fori paralleli alla direzione della velocità (presa statica). Essi sono posti in modo tale che la pressione all’ interno è pari alla pressione corrispondente al livello statico.Il tubo interno ha l’ estremità controcorrente (presa dinamica).
Generalmente di acciaio inox può essere di diverse misure, si va da lunghezze di qualche centimetro e diametro di qualche millimetro a lunghezze di un metro e diametro di qualche centimetro.
La parte perpendicolare al terreno è detta gambo, mentre quella orizzontale al terreno è detta testa e può essere lunga una ventina di diametri.

Figura 3 : tubo di Pitot , sezione laterale.
Lo strumento va puntato nella direzione opposta al verso del fluido di cui si
vuole misurare la velocità. Come si nota in figura 3 il tubo è chiuso nella parte finale del gambo da un manometro; il fluido entra dalla testa del tubo, ma una volta riempiti gambo e testa è come se lo strumento fosse chiuso nella parte frontale, e quindi il fluido si vede costretto a girare attorno alla punta della testa.Nella parte iniziale della testa si ha evidentemente velocità nulla (punto di ristagno ) e di conseguenza un massimo di pressione.Ad una distanza dalla punta della testa di circa 5-8 D (diametri) il fluido ha riacquistato la sua velocità, e qui grazie ai fori per la pressione statica viene presa la pressione suddetta.
![]()
Vediamo ora di risalire alla formula che mi permette di risalire al calcolo
della velocità W del fluido partendo dall’ equazione di Bernulli :
![]()
Innanzitutto individuiamo 2 sezioni, una all’ ingresso del tubo e una all’ altezza dei fori della pressione statica.
Vediamo quali termini dell’ equazione possiamo trascurare ; il lavoro l perché non presente all’ interno del nostro sistema , le perdite di carico R perché il tubo è costruito in modo ( bassa resistenza aerodinamica…) che possano essere trascurate.
Anche il termine g(z2-z1) può essere trascurato in virtù del fatto che la posizione dei fori per la presa statica e l’asse del tubo stesso sono alla stessa quota, e poi la velocità W1 nella sezione 1 in quanto l’ingresso è un punto di ristagno e quindi W1 = 0.
Quindi con le seguenti semplificazioni l’ equazione diventa :
![]()
da
cui :
![]()
Quindi
abbiamo che per determinare la W2 basta determinare la differenza di
pressione tre le due sezioni prese in esame.
Per
fare questo ci serviamo di un manometro.
Manometro a tubo inclinato
E’
un manometro a colonna di liquido impiegato per misurare differenze di
pressione molto piccole. Esso è formato da un serbatoio, sul quale grava la
pressione P1 e in cui pesca un tubo di vetro inclinato di un angolo
α e comunicante col recipiente a pressione P2 o lasciato alla
pressione atmosferica.Si ottiene così un allungamento della scala di misura
proporzionale a senα essendo il dislivello pari a lsenα dove l è lo
spostamento del menisco quando il manometro entra in pressione.
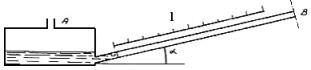
Figura 4: Manometro a tubo inclinato, sezione laterale.
Manometro differenziale a membrana
In questo manometro vi è un elemento sensibile costituito da una membrana deformabile sotto pressione, la quale trasmette il suo movimento ad un leveraggio
che aziona l’indice di una scala graduata (vedi figura 5).
I manometri a membrana sono utilizzati per misurare pressioni statiche relativamente basse (inferiori a 50 bar).
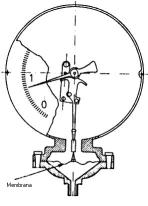
Figura 5: Manometro a membrana, sezione frontale.
A volte però al posto del leveraggio vengono usati trasduttori di pressione, cioè strumenti in cui la deformazione di una membrana produce un segnale elettrico che aziona l’indice di uno strumento o viene inviato ad un registratore o ad una apparecchiatura di controllo. A seconda di come il segnale elettrico viene prodotto si distinguono :
● trasduttori
piezoelettrici ,
che sono basati sulla proprietà delle sostanze piezoelettriche (quarzo) di emettere cariche elettriche quando vengono sottoposte a deformazioni meccaniche : tali cariche vengono raccolte su armature metalliche e producono un segnale di tensione proporzionale alla pressione (figura)
Figura 6: Trasduttore piezoelettrico, vista laterale.
● estensimetri o strain gauge ,
il cui funzionamento è basato su una variazione di resistenza derivante dalla deformazione di un elemento sensibile di tipo metallico.Dalla seconda legge di Ohm
risulta R = σ (L/A) per cui la resistenza di un conduttore è funzione, oltrechè della resistività, anche delle dimensioni (lunghezza e sezione ) del medesimo.Nel circuito di misura, nota la corrente, tale variazione di resistenza si traduce in una variazione di pressione proporzionale alla tensione.
Anemometro
Strumento per la misura della velocità del vento.L’ anemometro non viene usato solo in meteorologia, ma in senso più lato indica un misuratore di velocità di correnti gassose in un tunnel, gallerie aerodinamiche, condotti di impianti industriali, ecc. Esso, inoltre, installato a bordo degli aerei permette la misurazione della vera velocità di volo.
Si hanno due tipi di anemometri :
● a coppe
● a pale .
L’anemometro a coppe, usato soprattutto all’ aperto per misurazioni meteorologiche, è costituito da un mulinello che su tre o quattro bracci orizzontali porta altrettante coppe metalliche semisferiche.Investito dal vento che esercita una pressione maggiore sulla superficie concava delle coppe, il mulinello entra in rotazione girando sempre nello stesso senso qualunque sia la direzione del vento con una velocità proporzionale a quella del vento.
L’anemometro a pale è simile al precedente , salvo che ora il mulinello porta sei o otto palette orizzontali; questo anemometro è particolarmente usato per la misura della velocità alle bocchette di ventilazione degli impianti industriali di condizionamento e ventilazione.
Approfondimento
L’
impianto degli strumenti a capsula in un aereo.
Come avevamo accennato il tubo di Pitot è l’unico strumento per la misura di velocità di un aereo.Ma vediamo più in particolare la relazione tra l’ impianto dei dispositivi a bordo di un velivolo e gli strumenti precedentemente analizzati.
Gli strumenti a capsula in un aereo sono il variometro, l’altimetro, e l’ anemometro.
Sono chiamati strumenti a capsula perché il loro organo principale è appunto una capsula metallica dalle pareti sottilissime, che ha la proprietà di espandersi e contrarsi quando opportunamente sollecitata da differenze di pressione fra il suo interno e il suo esterno. Per questa ragione è a volte chiamata capsula differenziale.
Per far funzionare gli strumenti a capsula è pertanto necessario far loro pervenire quelle pressioni, la cui differenza di valore costituisce l’indice della grandezza da misure,che sono la pressione statica e la pressione dinamica.Ogni aereo deve perciò essere dotato almeno di una presa per la pressione statica, e di una per la pressione dinamica, dette appunto presa statica e presa dinamica.
La prima è ubicata sull’ aereo in una posizione tale per cui non venga influenzata dal moto, mentre la presa dinamica è disposta parallelamente all’ asse longitudinale dell’ aereo, in modo che la sua sezione possa captare tutta la sovrapressione generata dal moto, ma in una posizione nella quale non risenta della scia dell’ elica e di altri fattori di disturbo
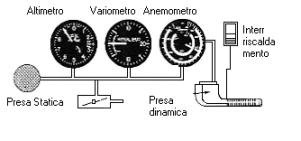
Figura 7: Strumenti di bordo a capsula di un aereo.
I costruttori di aeri possono adottare svariate soluzioni per la dislocazione delle due prese.Una soluzione consiste nell’ impiegare il tubo di Pitot, in cui la pressione d’impatto entra dall’apertura anteriore del tubo interno esposta al moto, mentre la pressione statica entra da una serie di fori praticati nella parete laterale del tubo esterno.Sui monorotori il tubo di Pitot è generalmente applicato sotto una seminala, mentre sui bimotori è applicato nella parte anteriore della fusoliera.
Una seconda soluzione è quella illustrata in figura , in cui si vede che la presa dinamica, è separata dalle prese statiche.Quando le prese statiche non sono situate sul tubo di Pitot , esse si trovano sui fianchi della fusoliera, una per lato , per compensare l’effetto di eventuali disallineamenti temporanei in manovra dell’ aereo rispetto al venti relativo.
Dalla figura si nota che tutti e tre gli strumenti ricevono la pressione statica, mentre solo l’ anemometro riceve la pressione dinamica.
Si nota inoltre che la presa dinamica è riscaldata elettricamente per prevenire o eliminare eventuali formazioni di ghiaccio, e che l’ impianto è dotato di una presa statica alternata da aprire in caso di ostruzione delle principali.
L’ anemometro o indicatore di velocità , è lo strumento che consente di misurare la velocità dell’ aereo relativa alla massa d’ aria che lo circonda .Come mostra la figura 8 è schematicamente costituito da una cassa a tenuta stagna, in collegamento con l’ esterno tramite una presa statica; all’ interno della cassa si trova la capsula, in collegamento con l’ esterno tramite la presa dinamica .
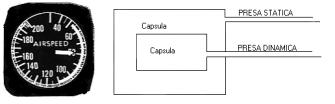
Figura 8: Indicatore di velocità di un aereo.
La capsula è collegata all’indice dello strumento da un’opportuna combinazione di leve e ingranaggi, i quali, oltre a trasformare il moto rettilineo di contrazione e dilatazione della capsula in moto rotatorio dell’indice,lo amplificano anche convenientemente.
Quando l’aereo è fermo al suolo, sia dalla presa statica sia dalla presa dinamica entra la sola pressione statica, e perciò le due pressioni all’interno e all’esterno della capsula sono uguali ; di conseguenza essa rimane nella sua posizione di riposo, e lo strumento segna zero.
Quando l’aereo comincia la corsa di decollo, da entrambe le prese continua a entrare la pressione statica, ma dalla presa dinamica entra anche la pressione dinamica generata dal moto, per cui all’interno della capsula si viene a trovare una pressione (pressione d’impatto) maggiore della pressione statica esistenze all’ esterno della capsula e questa si dilata.E’ ovvio che la dilatazione è tanto maggiore quanto maggiore è la presa dinamica, e quindi la velocità dell’aereo. Pertanto, l’indice dello strumento permette di leggere il valore della velocità del moto che provocato la dilatazione della capsula.
Venturimetro
Strumento di misura della portata transitante in una condotta, detto anche “contatore di Venturi”.
Il venturimetro è costituito da due tronchi, il primo convergente ed il secondo divergente vedi figura 9.
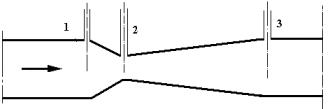
Figura 9 : Venturimetro , vista laterale
Come si può osservare in figura 9, lo strumento è costituito da tre
manometri situati nei tre punti indicati in figura (1,2,3), e da un tubo con
una brusca riduzione di sezione nella zona tra 1 e 2, e da un allargamento
molto più graduale alla sezione iniziale, tra 2 e 3.
Il manometro 3 non è di utilità diretta nella misura della velocità, in
quanto serve per controllare che la pressione sia ritornata la stessa che si ha
in 1 (di solito viene recuperata circa il 90% della potenza che c’è in uno) ;
questo è necessario in quanto il tubo di Venturi è uno strumento che non deve
dar luogo a perdite di carico lungo il circuito idraulico.
In questo caso viene calcolata la velocità media, mettendola in relazione
con la pressione, tramite l'equazione di continuità; tale equazione viene
scritta per il tubo di flusso che ha come sezione iniziale e finale le sezioni
1 e 2, e come profilo laterale lo stesso tubo.
Dall'equazione di Bernoulli, supposto il condotto orizzontale ed il fluido
incomprimibile, si ha:
![]()
Il problema, rispetto al tubo di Pitot, è che in questo caso compaiono due
velocità; si tratta quindi di esprimere una velocità in funzione dell'altra,
tramite una relazione ottenuta dall'equazione di conservazione della massa.
![]()
da cui:
![]()
dove A1 e A2 sono le aree delle
superfici delle sezioni di entrata e di uscita.
Se la densità r viene supposta costante (fluido incomprimibile),
è possibile semplificarla.
Trattandosi di sezioni circolari, la superficie è proporzionale al quadrato
dei raggi, quindi:
![]()
![]()
da cui si ricava la velocità W2
in funzione di W1:
![]()
Si sostituisce ora l'espressione della velocità W2 nell'equazione
:
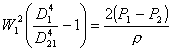
In questo modo si ottiene l'espressione della velocità W1:
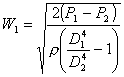
Anche nel caso del tubo di Venturi, per quanto riguarda la misura di
pressione su fluidi gassosi, si utilizza generalmente un micromanometro a tubo
inclinato, mentre nel caso di liquidi, si è soliti usare manometri a membrana.
Un possibile problema dei tubi di Venturi si verifica quando la strozzatura
della sezione 2 è troppo piccola; la velocità del liquido infatti aumenta
bruscamente, e di conseguenza diminuisce la pressione; se tale pressione scende
sotto la pressione di saturazione, il liquido vaporizza dando luogo ad
un fenomeno di cavitazione: si
formano delle interruzioni della continuità liquida, occupate dal vapore; i
risultati di questo fenomeno sono perdite di carico notevoli e formazione di
fenomeni turbolenti; quando la pressione torna a salire, le bolle collassano su
se stesse, e implodono provocando rumore e vibrazioni che possono danneggiare
il condotto.
I tubi di Venturi sono quindi progettati per un intervallo definito di
portate, in quanto se la portata è troppo piccola non avrò differenze di
pressioni misurabili, viceversa avverrà il fenomeno della cavitazione.
![]()
Diaframmi
e boccagli
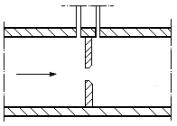
Figura 10: Diaframma , sezione laterale.
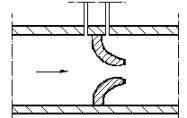
Figura 11: Boccaglio , sezione laterale.
Rotametro
I flussometri sono strumenti idonei alla misura di portate piccole o medie.Essi sono costituiti da un tubo di vetro conico entro cui si trova un galleggiante, che può avere sezione conica, come è indicato in figura 12 ,o sferica.
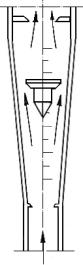
Figura 12: Rotametro, vista frontale.
Il rotametro è dispositivo verticalmente con l’entrata in basso e l’uscita in alto.La misura si basa sul fatto che l’aria, percorrendo il rotametro, investe il galleggiante e l’oltrepassa.Il galleggiante diventa per tanto un ostacolo che crea una perdita di pressione localizzata, dovuta al restringimento della sezione di passaggio.Si ottiene quindi un equilibrio tra la spinta dovuta alla differenza di pressione a monte e a valle del galleggiante ed il peso del galleggiante stesso.Essendo questo costante, se il flusso aumenta rispetto ad una certa condizione di equilibrio, si ha un incremento della caduta di pressione che provoca il sollevamento del galleggiante fino ad nuovo equilibrio.Si stabilisce allora una relazione tra la portata e la posizione del galleggiante .La posizione viene letta su una scala graduata incisa sul tubo di vetro o affiancata ad esso.
I rotametri richiedono una taratura rispetto a condizioni di pressione e di temperatura standard di riferimento.Con formule di correzione possono però essere utilizzati in condizioni di esercizio differenti.La portata che forniscono è comunque una portata di massa, espressa per lo più in volumi normali.
I rotametri possono anche essere utilizzati in relazioni con diaframmi per realizzare un misuratore in cui l’elemento primario per la misura della
portata è il diaframma, e il manometro differenziale e costituito da un rotametro la cui indicazione, proporzionale al flusso che lo attraversa e quindi alla caduta di pressione, dà il valore della portata che percorre la tubazione principale.
Misuratori a turbina
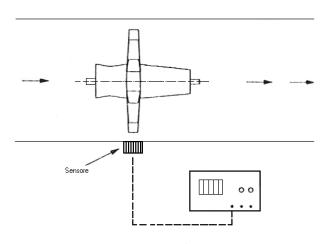
Figura 13:Misuratore a turbina, vista laterale.
Le turbine che operano sui liquidi sono dei misuratori di velocità media (di portata).
In un corpo cavo da montare in linea sulla tubazione è calettata una turbina che ruota
per effetto del flusso, compiendo nell’unità di tempo un numero di giri proporzionale alla portata.Di fronte alle palette della turbina è inserito un misuratore induttivo, che conta il numero di palette che gli passano davanti nell’unità di tempo.Le indicazioni digitali del trasduttore vengono convertite in un segnale analogico continuo proporzionale alla portata .I misuratori a turbina offrono un vastissimo campo di impiego, che a seconda delle dimensioni dell’ apparecchiava da frazioni di 1/min a 10000 1/min.