Scambio termico per irraggiamento
L’irraggiamento è, dopo conduzione e convezione, il terzo modo in cui può avvenire scambio termico tra due corpi.
In generale un qualsiasi corpo è soggetto simultaneamente ad un flusso di energia entrante in esso e ad uno uscente da esso, che sono gli effetti dell’interazione termica con l’ambiente in cui si trova. Se si considerano due corpi, ognuno di essi emetterà energia verso l’ambiente circostante, quindi ognuno di essi riceverà energia dall’altro corpo. Ovviamente queste energie saranno nel caso più generale diverse; se, infatti, fossero uguali non si vedrebbe alcuna variazione nello stato dei corpi, che recupererebbero la stessa energia persa.
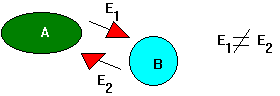
Fig. 1 : Scambio di energia tra due corpi
Questo discorso vale anche per le diverse parti di uno stesso corpo, che possono scambiarsi calore se sono affacciate; questo può avvenire solo nei corpi che presentano delle concavità. Per semplicità tali corpi non verranno considerati nella successiva analisi.

Fig. 2 : Esempio di corpo concavo
Il fenomeno dell’irraggiamento consiste nella classica propagazione delle onde elettromagnetiche. Come si può ricavare dalle due seguenti equazioni di Maxwell,
(valide in caso di assenza di sorgenti)
![]()
![]()
esse sono formate da campi elettrici e magnetici variabili. Questi campi nascono e si sostengono grazie ad effetti di induzione elettromagnetica. La Fig.3 rappresenta un’onda piana monocromatica, alla quale cioè possiamo associare una sola lunghezza d’onda e quindi una sola frequenza. Si ricordi infatti che queste due grandezze sono legate da una relazione di inversa proporzionalità:
![]()
dove l è la lunghezza d’onda, f la frequenza e c la velocità delle onde nel mezzo considerato. In particolare nel vuoto tale velocità è costante e vale c = 300000 km/s.
Negli altri mezzi essa vale![]() , dove n è il coefficiente di rifrazione del mezzo.
, dove n è il coefficiente di rifrazione del mezzo.
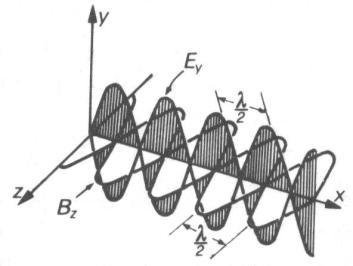
Fig. 3 : Onda elettromagnetica piana monocromatica
La Fig.3 mostra anche le posizioni reciproche dei campi in un’onda, che sono descritte dalle relazioni vettoriali
![]()
![]()
La prima mostra che ![]() e
e ![]() sono perpendicolari
tra loro, la seconda dà il vettore di propagazione.
sono perpendicolari
tra loro, la seconda dà il vettore di propagazione.
La monocromaticità delle onde elettromagnetiche è solo un’astrazione: infatti gli unici corpi reali che emettono ad una sola lunghezza d’onda (con buona approssimazione) sono le lampade laser. Tutti i corpi naturali e la maggior parte dei corpi artificiali emettono in banda larga, cioè distribuiscono l’energia emessa su un intervallo più o meno esteso di lunghezze d’onda. Tuttavia, come si può vedere dalla Fig.4, l’emissione non è continua, bensì l’energia è concentrata a certe lunghezze d’onda caratteristiche di ogni materiale; i picchi possono essere anche molto sottili, simili a righe, tanto che gli spettri di emissione vengono anche detti spettri a righe. Il fatto che le righe si collochino in punti ben precisi e fissi per un dato materiale deriva dal processo fisico che è alla base dell’emissione stessa.
Quando un corpo viene eccitato, gli elettroni ricevono energia e riescono a vincere la barriera che li separa dai livelli superiori. Tuttavia lo spostamento porta il sistema ad uno stato profondamente instabile, che costringe gli elettroni a tornare al punto di partenza. Naturalmente essi devono liberarsi dell’energia che avevano acquisito e si ha così l’emissione. Ma la separazione energetica dei vari livelli e la configurazione elettronica sono caratteristiche di ogni materiale e determinano univocamente il numero (numero di transizioni elettroniche a diversa energia permesse) e la posizione dei picchi di emissione. Si hanno così spettri con un basso numero di righe, come per l’idrogeno e gli elementi leggeri, e spettri con molte righe: quanto più un atomo è
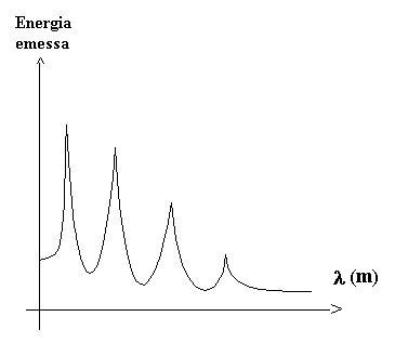
Fig. 4 : Energia emessa da un corpo reale in funzione della lunghezza d’onda
pesante, tanto più numerose sono le transizioni elettroniche permesse e tanto più lo spettro si avvicina a quello continuo.
Apparentemente l’emissione è uno dei fenomeni più evidenti che ci siano in natura, ma in realtà gran parte delle radiazioni si sottraggono alla nostra vista, perché non cadono nel visibile. A questo proposito è utile osservare lo spettro delle onde elettromagnetiche nella sua completezza. Facendo riferimento alla Fig.6, la radiazione visibile è la piccola striscia grigia che si colloca appena prima dei 10-6 m (0.4-0.7 nm). Si vede distintamente come i nostri occhi ci nascondano gran parte dei fenomeni elettromagnetici. Molte delle righe di emissione di tutti gli elementi possono essere individuate solo con l’ausilio di strumentazione apposita, poiché cadono fuori dalla zona di sensibilità della vista umana.
Nello stesso modo in cui emette, un corpo può anche assorbire radiazione elettromagnetica; questo fenomeno è legato agli stessi processi di transizioni elettroniche coinvolti nel caso precedente, quindi le energie in gioco sono le stesse e così le lunghezze d’onda. Si può allora concludere che un corpo assorbe alle stesse frequenze alle quali emette.
Se un corpo è colpito da luce bianca uniforme, parte dell’energia è riflessa, parte assorbita e parte trasmessa. Rappresentando quella trasmessa si nota che alle stesse lunghezze d’onda cui corrispondono i picchi di emissione vi sono ora delle buche di assorbimento. In particolare, se E è l’energia della radiazione incidente, vale la relazione
![]()
Il fenomeno dell’assorbimento influisce notevolmente sull’irraggiamento; infatti, per avere un buono scambio di calore tra due o più corpi è necessario che il mezzo che li separa sia trasparente. Per capire come questo sia importante è sufficiente osservare l’effetto della materia sulla intensità dell’onda.
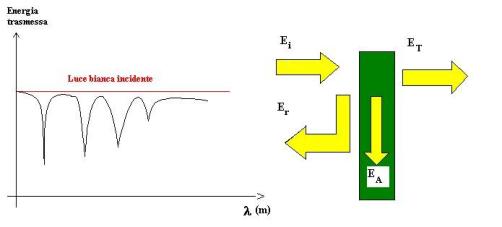
Fig. 5 : Assorbimento di energia
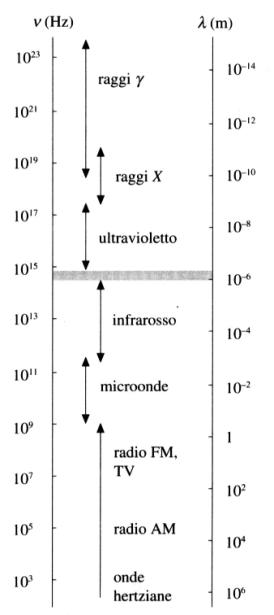
Fig. 6 : Spettro delle onde elettromagnetiche
Se una radiazione di intensità ![]() colpisce uno strato
di materiale di spessore X l’intensità dell’onda trasmessa è data da
colpisce uno strato
di materiale di spessore X l’intensità dell’onda trasmessa è data da
![]()
dove b è il coefficiente di estinzione. Osserviamo che la decrescita è esponenziale, quindi se il b del mezzo è troppo elevato la radiazione si estingue velocemente e gli interscambi tra i corpi sono notevolmente ridotti.
Questo coefficiente di estinzione assume valori diversi per le varie sostanze, ma non è una costante: esso dipende dalla lunghezza d’onda della radiazione incidente.
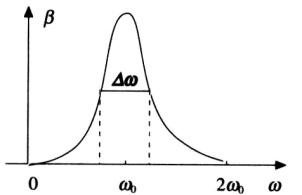
Fig. 7 : Coefficiente di estinzione e risonanza
Come si può vedere dalla Fig.7, dove ![]() , attorno a l ben
precise (nella figura ne è rappresentata una sola), fissate dalla
configurazione elettronica della sostanza, il b
è soggetto a risonanza e si ha un assorbimento anomalo: questa è l’origine
delle righe di assorbimento.
, attorno a l ben
precise (nella figura ne è rappresentata una sola), fissate dalla
configurazione elettronica della sostanza, il b
è soggetto a risonanza e si ha un assorbimento anomalo: questa è l’origine
delle righe di assorbimento.
Il colore che la nostra vista associa ad un corpo è quello della luce che esso riflette: in essa ci sono dunque tutte le componenti cromatiche eccetto quelle che esso assorbe. Ad esempio l’acqua è opaca per quasi tutto lo spettro, tranne per una finestrella nel visibile: essa riflette nel verde-azzurro. Per questo, ad esempio, la luce rossa perde già il 90% della sua intensità a 3 m di profondità. Se l’acqua non assorbisse tutte queste lunghezze d’onda assumerebbe per l’uomo una colorazione molto marcata. Una singolare coincidenza è il fatto che il verde-azzurro sia la zona di maggiore sensibilità dell’occhio umano, tanto da far pensare che l’uomo abbia avuto antenati marini!
Come si è visto precedentemente, lo spettro delle onde elettromagnetiche è molto vasto, ma per descrivere i fenomeni terrestri è possibile restringere il campo delle lunghezze d’onda d’interesse a quelle maggiori della minima l a cui emette il Sole.
Quest’ultima cade nell’ultravioletto e lo divide in due parti: quella interna alla zona d’interesse viene detta U.V.A. Si osservi in particolare che rimangono escluse da questo campo anche le radiazioni ionizzanti, le quali hanno un’alta energia e riescono a strappare elettroni agli atomi. Così facendo esse rompono dei legami chimici e creano dei radicali liberi, che sono molto reattivi e danno origine a composti in grado di provocare la morte cellulare negli organismi viventi.
La figura di emissione di un corpo (Fig.4) dipende fortemente dalla temperatura: all’aumentare di quest’ultima il corpo emette a l sempre minori. Se si considera
l’inviluppo dei picchi (si approssima cioè il corpo ad un corpo nero, come si vedrà), esso presenta un massimo, la cui posizione è legata alla temperatura dalla relazione
![]() .
.
Come vedremo questa è detta legge di Wien.
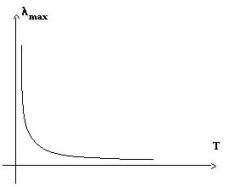
Fig. 8 : Legge di Wien
Questa legge stabilisce una corrispondenza tra temperatura e lunghezza d’onda di maggiore emissione, tanto che in colorimetria si parla di temperatura di colore: è la temperatura di un corpo il cui spettro ha l’emissione coincidente con quella della lampada. Ad esempio se la temperatura di colore di una lampada è alta, essa emette nel verde-azzurro, se è bassa si ha luce rossastra.
Analisi energetica
In vista di analizzare la figura di emissione di un corpo, è necessario
introdurre alcune grandezze energetiche fondamentali. Detta ![]() la potenza emessa
per unità di superficie ( W/m2 )(si può osservare per quanto
detto precedentemente che essa è funzione della temperatura), si definisce il potere
emissivo monocromatico o specifico e
come
la potenza emessa
per unità di superficie ( W/m2 )(si può osservare per quanto
detto precedentemente che essa è funzione della temperatura), si definisce il potere
emissivo monocromatico o specifico e
come
![]() (W/m3)
(W/m3)
Allora
![]()
e ![]() viene detto anche potere
emissivo integrale, in quanto rappresenta l’effetto cumulativo su tutto lo
spettro.
viene detto anche potere
emissivo integrale, in quanto rappresenta l’effetto cumulativo su tutto lo
spettro.
Si consideri ora un corpo e siano: ![]() la potenza incidente,
la potenza incidente,![]() la potenza riflessa,
la potenza riflessa, ![]() la potenza assorbita,
la potenza assorbita,
![]() la potenza trasmessa.
Si può subito osservare (vedere Fig.5) che
la potenza trasmessa.
Si può subito osservare (vedere Fig.5) che
![]()
I rapporti
![]()
![]()
![]()
prendono il nome rispettivamente di coefficienti di riflessione, trasmissione e assorbimento.
Allora
![]() .
.
Si osservi infine che questi coefficienti sono effettivamente dei numeri puri, ma comunque variabili con la lunghezza d’onda della radiazione incidente.
Corpo nero
Si è già detto come la figura di emissione sia segnata da alcuni picchi nei quali si concentra la maggior parte dell’energia. A causa delle difficoltà nella descrizione analitica del potere emissivo per i corpi reali, si usa introdurre una costruzione teorica: si definisce corpo nero un ipotetico materiale con elettroni eccitabili ad infiniti stati. Esso viene ad essere un corpo che ad ogni temperatura assorbe completamente la radiazione che gli arriva a qualsiasi lunghezza d’onda, cioè
![]()
![]()
Il potere emissivo specifico per un tale corpo viene ad essere l’involucro esterno dei picchi di un corpo reale e assume la forma visibile in Fig.9.
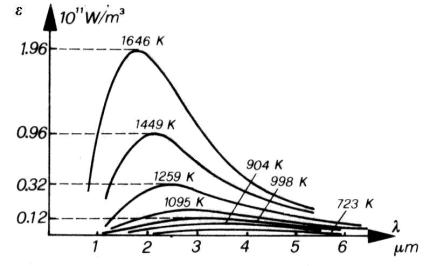
Fig. 9 : Potere emissivo specifico del corpo nero alle varie temperature
Si osservi infatti che in queste condizioni si ha la massima emissione possibile.
Per il corpo nero si usa convenzionalmente il pedice ‘0’
dopo le varie grandezze energetiche per distinguerle da quelle dei corpi reali:
ad esempio il potere emissivo monocromatico si chiama ![]() .
.
I corpi neri perfettamente fedeli alla definizione sono praticamente irrealizzabili; una realizzazione pratica accettabile è visibile in Fig.10: il corpo nero è il punto C.
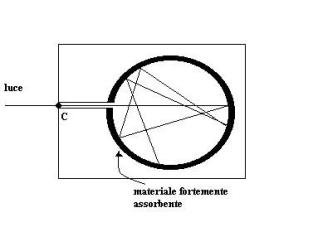
Fig. 10 : Esempio di corpo nero
E’ possibile descrivere in modo preciso il comportamento del corpo nero grazie ad alcune leggi.
Legge di Planck
Questa legge afferma che il potere emissivo specifico di un corpo nero è esprimibile nella forma
![]()
dove le due costanti valgono
![]()
![]()
Questa espressione si ottiene approssimando il corpo emettitore ad un insieme di oscillatori armonici e sposando la fisica quantistica, che associa ad essi dei livelli energetici discreti. Infatti la fisica classica, concedendo un intervallo continuo di energie, portava alla legge di Rayleigh-Jeans, che si scosta in modo netto dal risultato sperimentale, praticamente coincidente con la previsione di Planck.
Legge
di Wien
Come anticipato precedentemente, questa legge mette in relazione la lunghezza
d’onda del picco di emissione con la temperatura.
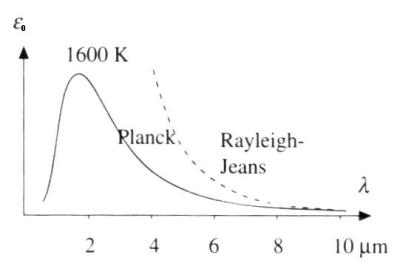
Fig. 11 : Legge di Rayleigh-Jeans e Planck: la curva sperimentale
coincide con quella di Planck
In particolare
![]() .
.
L’inversa proporzionalità è chiaramente visibile anche in Fig.9.
Questa espressione è analiticamente ottenibile dalla legge di Planck (per il calcolo si veda la Appendice 1), ma fu enunciata da Wien trent’anni prima che quest’ultima venisse formulata.
Legge di Stefan-Boltzmann
Integrando il potere emissivo specifico di Planck su tutto lo spettro (vedere l’Appendice 2) si ottiene questa legge, secondo la quale
![]()
dove la costante di proporzionalità è la costante di
Stefan-Boltzmann e si indica con ![]() .
.
Corpi grigi e corpi reali
L’astrazione applicata nella definizione del corpo nero è radicale; si può concedere un po’ di più definendo i corpi grigi, per i quali
![]() ;
; ![]()
il coefficiente di assorbimento è minore di 1, ma costante a
tutte le lunghezze d’onda e a tutte le temperature.Tuttavia in generale i corpi
reali non sono grigi e per essi vale che ![]() . In ambito tecnico i corpi vengono considerati come grigi.
Si può però osservare che quanto più un materiale è chimicamente complicato,
tante
. In ambito tecnico i corpi vengono considerati come grigi.
Si può però osservare che quanto più un materiale è chimicamente complicato,
tante
più sono le sue righe spettrali, tanto più il suo spettro si avvicina a quello del corpo nero. Per i corpi grigi vale in generale la relazione
![]() (grigiezza rispetto al potere e)
(grigiezza rispetto al potere e)
dove e è il coefficiente di emissione per i corpi grigi.
Quindi l’emissione non è più la massima possibile, ma è ridotta del 20%.(Fig.12)
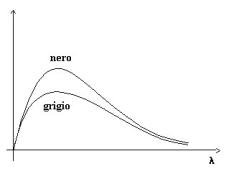
Fig. 12 : Corpo nero e grigio a confronto
Si consideri ora una superficie chiusa cava a temperatura
costante ![]() . Si immerga in essa un corpo nero: a regime esso ha
temperatura
. Si immerga in essa un corpo nero: a regime esso ha
temperatura ![]() e vale
e vale
![]()
Si tolga il corpo nero e vi si immerga un corpo grigio:
anch’esso si porta a ![]() e a regime
e a regime
![]()
da cui si ricava
![]() .
.
Allora per il corpo grigio è sufficiente porre il
coefficiente ![]() davanti
all’espressione di Stefan-Boltzmann per avere il potere emissivo integrale.
davanti
all’espressione di Stefan-Boltzmann per avere il potere emissivo integrale.
Emissione angolare
Non si è ancora detto nulla sulla distribuzione nelle varie direzioni dello spazio dell’energia emessa. E’ necessario allora introdurre un’altra grandezza, il potere emissivo angolare i, definito come la potenza emessa per unità di superficie su un angolo solido dW, cioè
![]() .
.
L’unità di misura di i è ![]() poiché l’angolo
solido si misura in sterad.
poiché l’angolo
solido si misura in sterad.
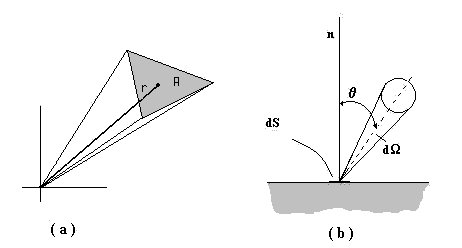
Fig. 13 : Angolo solido
Con l’aiuto della Fig.13 ( a ) è possibile ricordare la definizione dell’angolo solido:
![]()
da cui si può facilmente ricavare che ![]() . L’angolo solido totale misura 4p.
. L’angolo solido totale misura 4p.
Il potere emissivo angolare viene convenzionalmente rappresentato in coordinate polari: l’inviluppo delle sue ampiezze è detto solido fotometrico.
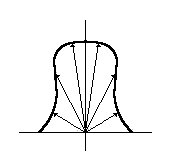
Fig. 14 : Esempio di solido fotometrico
In questi diagrammi l’angolo con l’orizzontale rappresenta la direzione di emissione, la distanza della curva dall’origine rappresenta l’ampiezza del potere emissivo angolare. Spesso essi sono simmetrici rispetto all’asse verticale, ma non è la regola.
Per il corpo nero vale la legge di Lambert, secondo la quale
![]()
dove ![]() è il valore massimo
di
è il valore massimo
di ![]() raggiunto sulla verticale.
raggiunto sulla verticale.
Quindi il solido fotometrico del corpo nero è una sfera.
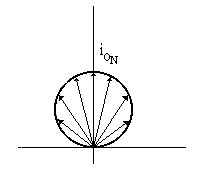
Fig. 15 : Solido fotometrico del corpo nero
Un corpo non nero ma che mantiene un comportamento alla Lambert presenta sfere più piccole, spesso di forma vagamente ovoidale, come nella Fig.16.
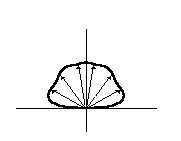
Fig. 16
Per un corpo non nero che emette in modo uniforme in tutte
le direzioni il solido fotometrico è una semisfera. A parità di ![]() vale
vale ![]() (Fig.17).
(Fig.17).
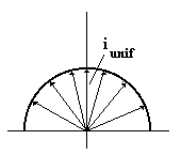
Fig. 17 : Solido fotometrico uniforme di un corpo non nero
Per i corpi grigi, vale la condizione
![]()
detta criterio di grigiezza rispetto al potere emissivo.
Infine, i corpi reali non approssimabili né a corpi neri né a corpi grigi presentano solidi fotometrici a volte molto complessi, come quelli visibili in Fig.18.
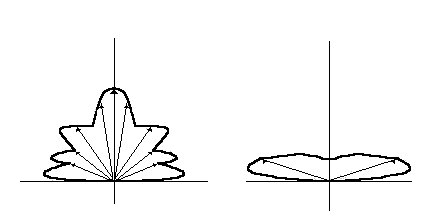
Fig. 18
Legge di Prevost
Questa legge, anche se non venisse citata, non creerebbe nessun problema, in quanto ormai suona ovvia a chiunque, ma quando venne enunciata era tutt’altro che scontata. Essa dice che
![]() .
.
Osservando che
![]() e
e ![]()
si ottiene
![]() .
.
Intensità
Per definire questo concetto è necessario inserirsi nell’ottica di chi riceve la radiazione: l’intensità rappresenta sempre una potenza per unità di superficie, ma questa volta è una potenza ricevuta.
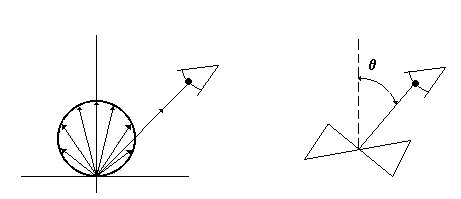
Fig. 19
Si supponga che la luce di un corpo nero (alla Lambert) colpisca un osservatore.
Facendo riferimento alla Fig.19, si può osservare che l’angolo dal quale l’occhio vede arrivare la luce influisce sulla superficie che viene effettivamente vista.
Infatti all’osservatore sembrerà che la luce arrivi da un superficie, che chiamiamo apparente, diversa da quella reale. In particolare varrà la relazione
![]() .
.
Ma, se l’emissione avviene fedelmente alla legge di Lambert, la potenza che viene irraggiata all’inclinazione q è diminuita dello stesso fattore cosq. Allora si ha cosiddetta Legge di Lambert sull’intensità, secondo la quale
![]() .
.
Appendice 1 – Legge di Wien
La legge di Wien è facilmente ottenibile dalla legge di Planck, basta infatti calcolare l’ascissa del massimo del potere emissivo:
![]() ( legge di
Planck )
( legge di
Planck )
Dobbiamo ora imporre che ![]() :
:
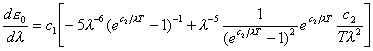
Ponendo ![]() si ottiene
si ottiene
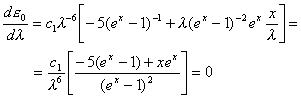
La condizione è verificata quando si annulla il numeratore:
![]()
Si tratta di un’equazione trascendente, che necessita di una risoluzione tramite approssimazione successiva. Il risultato è che la condizione è verificata per due valori: 0 (che non è accettabile) e un numero molto vicino a 5.
Allora
![]()
Stimando meglio il valore di x si ottiene che il prodotto
vale effettivamente ![]()
Appendice 2 – Legge di Stefan-Boltzmann
Per ottenerla è sufficiente integrare il potere emissivo specifico del corpo nero, dato dalla legge di Planck, su tutto lo spettro delle lunghezze d’onda.
![]()
Ponendo ![]() si ha
si ha ![]() , quindi
, quindi
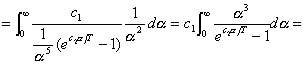
Conviene ora porre ![]() ; allora
; allora ![]()
![]()
Osservando che ![]() si ha infine
si ha infine
![]()
Quindi risulta
![]() .
.
Appendice 3 – Tabelle
Indice di rifrazione a 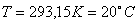
|
|
n |
|
|
Solidi |
Balsamo del Canada |
1,528 |
|
Calcite |
1,658 |
|
|
Crown dispersivo |
1,520 |
|
|
Flint pesante |
1,650 |
|
|
Quarzo amorfo |
1,458 |
|
|
|
Vetro pesantissimo |
1,890 |
|
Liquidi |
Acetone |
1,359 |
|
Acqua |
1,333 |
|
|
Alcool etilico |
1,361 |
|
|
Benzolo |
1,502 |
|
|
Etere etilico |
2,352 |
|
|
Solfuro di Carbonio |
1,627 |
|
|
Gas |
Anidride carbonica |
1,000448 |
|
Aria |
1,000292 |
|
|
Azoto |
1,000296 |
|
|
Elio |
1,000036 |
|
|
Idrogeno |
1,000132 |
|
|
Ossigeno |
1,000271 |
|
Coefficiente di assorbimento di superfici pulite
|
|
Temperatura(K) |
a |
|
Alluminio |
520 |
0.04 |
|
900 |
0.06 |
|
|
Amianto |
600 |
0.95 |
|
Cromo |
320 |
0.08 |
|
830 |
0.26 |
|
|
Ferro |
420 |
0.05 |
|
1300 |
0.37 |
|
|
Ghiaccio secco |
270 |
0.97 |
|
Nichel |
700 |
0.09 |
|
Rame |
370 |
0.02 |
|
Tungsteno |
300 |
0.03 |
|
3500 |
0.35 |
![]()
![]()