Esercizi sul 1° Principio della Termodinamica
Gli esercizi qui proposti sono caratterizzati da un recipiente ben definito, in modo da individuare facilmente il sistema che verrà trattato di volta in volta.
Per risolvere questi esercizi, è necessaria la presenza di qualche entità all’interno del sistema, e che la stessa sia soggetta a trasformazioni fisiche.
Esercizio n°1.
Consideriamo un contenitore termicamente isolato, tanto da poter supporre che lo scambio di calore fra sistema e ambiente sia nullo ( Q = 0 ): in tal modo vengono trascurati i fenomeni ai bordi.
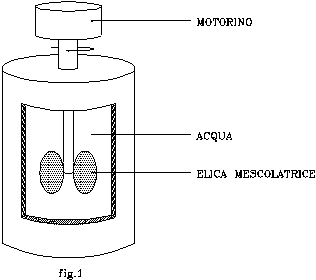
Nel recipiente di fig.1 sono contenuti 100 l di H2O agitati mediante un’elica calettata ad un motorino elettrico.
Si consideri
che la trasformazione avviene in condizioni
di pressione costante p =
![]() .
.
Sia L![]() = 0.5 CV la potenza erogata dal motore ( dove L
= 0.5 CV la potenza erogata dal motore ( dove L![]() =
= ![]() = P ) e
sia t =20min il tempo per cui lo stesso viene mantenuto in funzione.
= P ) e
sia t =20min il tempo per cui lo stesso viene mantenuto in funzione.
Determinare la variazione di energia interna DU del sistema in questione.
Inoltre,
sapendo che il calore specifico dell’acqua vale cp= 4187.0 ![]() alla pressione
atmosferica ( vedi tab.7 ), e che la temperatura iniziale del sistema
è Tin = 20°C,
calcolare la temperatura finale ( Tf ) al termine del
mescolamento.
alla pressione
atmosferica ( vedi tab.7 ), e che la temperatura iniziale del sistema
è Tin = 20°C,
calcolare la temperatura finale ( Tf ) al termine del
mescolamento.
Soluzione
esercizio n°1.
Normalizziamo i dati dell’esercizio in conformità alle unità di misura specificate dal SI ( vedi tab.1, tab.2, tab.3 ):
P = ![]() CV = 368
W ,
(1)
CV = 368
W ,
(1)
t = ![]() min = 1200s ( dato
che 1min = 60s ) , (2)
min = 1200s ( dato
che 1min = 60s ) , (2)
M = ![]() = 100kg ,
(3)
= 100kg ,
(3)
![]() . (4)
. (4)
![]()
Usiamo il 1° Principio della Termodinamica.
Sapendo che il calore scambiato dal sistema con l’ambiente è nullo e che il lavoro che andiamo calcolando è negativo ( dato che è eseguito sul sistema ), otteniamo una variazione positiva di energia interna:
![]() =
= ![]() . (5)
. (5)
Usando la (5), calcoliamo ora la variazione specifica di energia interna ( rispetto alla massa del corpo in esame ):
![]() .
(6)
.
(6)
Inoltre, ricordando la definizione di calore specifico:
![]() , (7)
, (7)
utilizzando le (4), (6), (7), otteniamo:
![]() .
(8)
.
(8)
Quindi, come era prevedibile, il sistema ha subito un aumento dell’energia interna e un rispettivo innalzamento della temperatura.
Esercizio
n°2.
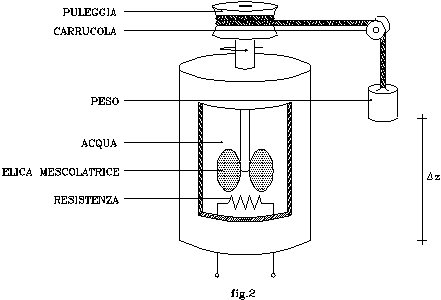
Sia dato nuovamente il recipiente di fig.1. In questo caso, però, l’elica mescolatrice sia azionata mediante un sistema a puleggia schematizzato in fig.2: l’albero viene messo in rotazione dalla caduta verticale di un peso di massa M=100kg ; questi è collegato alla puleggia per mezzo di una fune avvolta nella scanalatura della stessa, e passante attraverso una carrucola.
Il peso, in moto verso il basso (dovuto alla forza di gravità terrestre ), subisce una caduta di quota Dz ; dove con z si intende l’asse avente come direzione quella del grave in caduta, origine al livello del mare, e verso quello uscente dalla superficie terrestre.
Inoltre, all’interno del recipiente, sia presente un circuito elettrico composto da una resistenza R = 0.2 W, i cui capi siano collegati a cavetti uscenti dal contenitore.
La resistenza, sia isolata elettricamente dal fluido presente nel recipiente; esso contenga un volume V =100 l di H2O.
Il circuito elettrico, sia percorso da una corrente di intensità i = 6 A per un tempo t = 5 min .
Determinare il valore della caduta di quota del grave, supponendo che l’effetto prodotto dal riscaldamento di origine elettrica ( dovuto alla dissipazione sulla resistenza ) sia equivalente a quello di origine meccanica ( dovuto al mescolamento dell’elica ).
Soluzione
esercizio n°2.
Conformiamo le unità di misura dei dati a quelle del SI:
t = ![]() .
(9)
.
(9)
Procediamo utilizzando l’ipotesi secondo cui le energie di natura differente immesse nel sistema si equivalgono.
La variazione
di energia fornita dal circuito elettrico è data dalla legge di Joule ( che descrive la dissipazione di potenza
sotto forma di calore ceduto, da parte di una resistenza percorsa da corrente )
P = R i2 ;
dato che ci occorre la quantità di calore, moltiplichiamo la potenza ottenuta
per il tempo t (9)
, perciò:
![]() .
(10)
.
(10)
Considerando che il lavoro eseguito sul
sistema è nullo, l’aumento dell’energia interna ![]() per effetto Joule
è:
per effetto Joule
è:
![]() .
(11)
.
(11)
La variazione di energia ![]() determinata dall’
elica mescolatrice, è di natura meccanica: il lavoro compiuto sul sistema,
equivale alla variazione di energia potenziale Ep = M g Dz del grave dovuta alla caduta di quota.
determinata dall’
elica mescolatrice, è di natura meccanica: il lavoro compiuto sul sistema,
equivale alla variazione di energia potenziale Ep = M g Dz del grave dovuta alla caduta di quota.
Quest’ultima
avrà segno negativo dato che il peso decresce in altitudine.
Inoltre, il
calore fornito è nullo, perciò:
![]() . (12)
. (12)
Infine, uguagliando (11) e (12):
![]() ,
(13)
,
(13)
![]() ,
(14)
,
(14)
![]() . (15)
. (15)
Esercizio n°3.
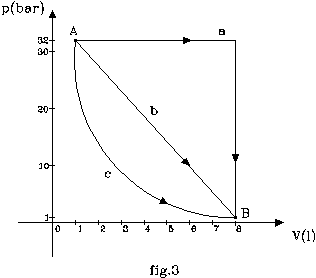
Si consideri un gas perfetto che compie una trasformazione da uno stato
fisico A ad uno B, individuati sul diagramma p-V ( fig.3 ) .
La
variazione di stato del gas avvenga da A verso B (espansione) avendo a
disposizione tre possibili percorsi:
a)
Trasformazione
isobara + isocora: a p (pressione) costante sul 1°tratto, a V (volume) costante sul 2°.
b)
Trasformazione
lineare: V e p variano linearmente.
c)
Trasformazione
adiabatica: di equazione ![]() (16)
(dove v è un volume per unità di massa).
(16)
(dove v è un volume per unità di massa).
Inoltre, il
processo sia quasi statico.
Dati i
valori di pressione e volume del gas agli stati A e B:
pa = 32 bar , pb = 1 bar , Va = 1 l , Vb = 8 l ,
determinare il lavoro eseguito per ogni trasformazione e fornire considerazioni sui risultati ottenuti.
NB:
Definizione: si dice trasformazione
adiabatica quel passaggio di stato per cui, considerando il percorso seguito,
localmente la quantità di calore scambiata fra sistema e ambiente è nulla Q = 0.
Dalla definizione, si deduce che è condizione
necessaria la conoscenza puntuale di tale trasformazione.
Questa proprietà è riscontrabile solamente nei processi quasi statici:
processi in cui ogni variazione infinitesima è quantificabile e rappresentabile
graficamente con una linea continua.
Occorre quindi molta attenzione quando si
trattano trasformazioni adiabatiche perché, affermando che il calore scambiato durante il processo è Q = 0 , si trascura il fatto che ciò è vero
localmente punto per punto.
Tale imprecisione può portare a
considerazioni errate, anche di notevole rilevanza, sul sistema in esame.
Esempio:
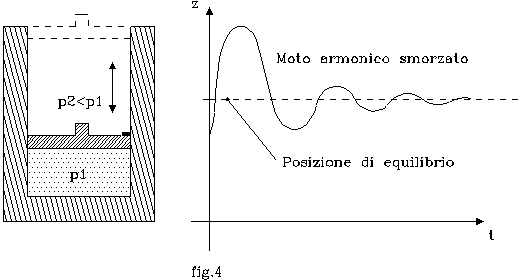
Sia dato un cilindro termicamente isolato ( fig.4
).
Al suo interno sia presente un gas mantenuto
alla pressione p1 da un pistone, bloccato tramite un fermo.
La pressione del fluido all’esterno p2 sia minore di p1.
Se ad un certo istante il fermo viene tolto, il pistone accelera bruscamente verso l’alto (relativamente alla differenza Dp = p1 - p2 ), raggiunge una estensione massima, ed infine oscilla di moto armonico smorzato attorno alla posizione di riposo (per cui Dp = 0).
Una trasformazione del genere non è quasi statica data la rapidità della stessa; quindi occorre una forza F agente dall’esterno che impedisca accelerazioni brusche e che decresca di quantità infinitesime fino a portare il pistone nella posizione di equilibrio.
Soluzione
esercizio n°3.
In generale possiamo dire che la grandezza
incognita dipende dal cammino eseguito dato che non è caratterizzata da una
forma differenziale esatta.
Questo, in prima approssimazione, ci porta ad
affermare che dovremo ottenere tre risultati differenti.
Conformiamo le unità di misura dei dati a quelle del SI ( tab.5 ):
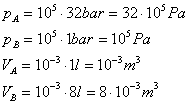
Calcoliamo il
lavoro sviluppato lungo il percorso c) (Lc).
Consideriamo l’espressione del lavoro per
unità di massa in forma integrale, sapendo che equivale all’area sottesa dalla
curva c):
![]() (17)
(17)
o meglio, dovendo calcolare il lavoro
effettivo:
![]() . (18)
. (18)
Sapendo che la relazione (16) descrive analiticamente il percorso c), troviamo il valore della costante imponendo la condizione di passaggio per il punto A:
![]() , (19)
, (19)
perciò, riscrivendola:
![]() ;
(20)
;
(20)
lo stesso discorso si poteva sviluppare per il punto B.
Svolgendo l’integrale (18) utilizzando (19) e (20), otteniamo:
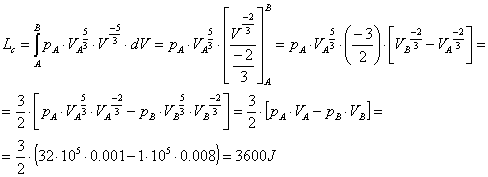 (21)
(21)
Dato che quella considerata è una trasformazione adiabatica, dal 1°Principio della Termodinamica si ha:
![]() . (22)
. (22)
Si noti che la variazione di energia del sistema è negativa dato che il lavoro è eseguito dal sistema.
Esaminiamo il cammino a).
Il lavoro eseguito è semplicemente dato dall’area del rettangolo sottesa dalla curva:
![]() ; (23)
; (23)
la variazione di energia non dipende dal percorso eseguito, perciò è la stessa anche per la trasformazione a).
Dalle (22) e (23):
![]() (24)
(24)
che è il calore assorbito dall’ambiente necessario per sviluppare lavoro durante il processo a).
Dal punto di vista del lavoro svolto, si può dire che questa trasformazione è migliore della c).
Esaminiamo il cammino b).
Il lavoro eseguito è dato dall’area del trapezio sottesa dalla curva, pertanto:
![]() . (25)
. (25)
Analogamente al caso precedente,dalle (22) e (25):
![]() (26)
(26)
che è il calore assorbito dall’ambiente necessario per sviluppare lavoro durante il processo b).
Come ci si poteva aspettare, dato che l’area sottesa dalla curva b) era visibilmente minore di a), il lavoro eseguito dall’ultima trasformazione è stato peggiore rispetto alla precedente (considerando il fatto che è stato richiesto meno calore dall’ambiente).
Esercizio
n°4.
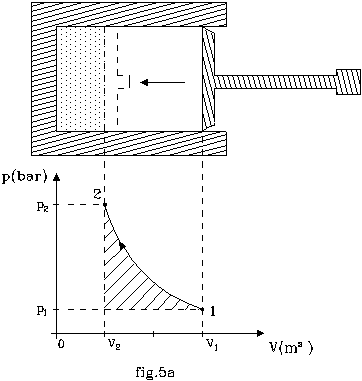
Sia dato un cilindro al cui interno sia presente aria mantenuta a pressione p1 = 1bar e volume iniziale V1 = 1m3 da uno stantuffo in equilibrio con l’atmosfera esterna ( fig.5a ).
Lo stesso venga azionato manualmente in modo da comprimere l’aria molto lentamente, per ottenere una trasformazione quasi statica.
Tale trasformazione avvenga a temperatura costante mediante l’utilizzo di un serbatoio refrigeratore ( per compensare l’aumento di energia interna del sistema ).
La
compressione prosegua fino a che il volume raggiunto dall’aria ( V2
) non sia pari ad un terzo del volume iniziale (V2 = 1/3 V1 ).
a) Determinare la pressione finale ( p2 ) all’interno del sistema ed il lavoro svolto sullo stesso dall’azione manuale.
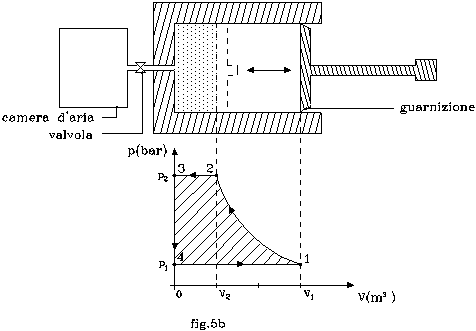
b) Ora si supponga che sul fondo del cilindro ci sia una valvola ( fig.5b ) che connetta il sistema iniziale ad una camera d’aria. Tale valvola sia in grado di favorire il flusso dell’aria solo verso l’esterno e solo se la pressione raggiunta nel cilindro sia pari a p2. Supponendo che la spinta dello stantuffo continui a fine corsa, e che successivamente venga riportato nella posizione di partenza, descrivere cosa avviene nel sistema e determinare il nuovo lavoro manuale svolto sullo stesso.
Si assuma inoltre che lo stantuffo sia munito di una guarnizione che funga da valvola: durante la fase di compressione non lasci fluire l’aria interna verso l’esterno, in fase di ritorno permetta a quella esterna di entrare.
Soluzione esercizio n°4.
a)
Conformiamo le unità di misura dei dati a quelle del SI ( tab.5 ):
![]()
Nel punto 1 (relativo al
grafico di fig.5a), lo stantuffo resta in equilibrio perché la pressione
interna dell’aria (p1)
bilancia perfettamente la pressione esterna dell’atmosfera: questo implica che
tutto il lavoro svolto sul sistema è dato dalla somma di quello compiuto
manualmente e quello svolto dall’atmosfera (dato che se non ci fosse dovremmo
imprimere più forza sullo stantuffo).
Quindi il lavoro manuale che andiamo cercando è rappresentato da tutta
l’area sottesa dalla curva fra 1 e 2, tranne quella del rettangolo di base V1
- V2 e altezza p1:
![]() .
(27)
.
(27)
Inoltre, in precedenza, abbiamo assunto T = cost; dal 1° Principio della Termodinamica:
![]() ,
(28)
,
(28)
si deduce che la trasformazione 1-2 è descritta da un’ iperbole
equilatera (dato che l’esponente su V nella (28) vale 1).
Imponiamo il passaggio della stessa per il punto 1 trovando il valore
della costante:
![]() ,
(29)
,
(29)
risostituendo nella
(28):
![]() .
(30)
.
(30)
Risolviamo la (27) utilizzando la (30):
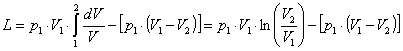 , (31)
, (31)
![]() . (32)
. (32)
Dato che il prodotto pV è costante lungo la curva, calcolo p2:
![]() ,
(33)
,
(33)
![]() . (34)
. (34)
b)
Arrivati al punto 2, continuando a premere sullo stantuffo, la valvola si apre ed istantaneamente l’aria viene espulsa tutta all’esterno, nella camera d’aria.
La caduta di volume del gas è rappresentato da un’isobara (tratto 2-3).
Non appena lo stantuffo viene ritratto di poco, la valvola si richiude; perciò, all’interno del cilindro, cala bruscamente la pressione poiché non c’è più aria (tratto 3-4).
Però, la guarnizione del pistoncino, è costruita in modo da permettere la immissione d’aria nuova in fase di recupero; così si torna a creare un sistema a pressione atmosferica e volume V1 (tratto 4-1).
Se però osserviamo quanto è avvenuto, ci accorgiamo che il gas di partenza non è più presente nel nuovo sistema (è stato rinchiuso nella camera d’aria); quindi si dice che siamo passati da un sistema chiuso ad uno aperto.
Qui non vale più il 1° Principio della Termodinamica (che è impostato sulla energia interna del sistema); si deve perciò ricorrere ad una nuova grandezza, l’entalpia (che tiene in considerazione non solo il sistema, ma anche l’ambiente che lo circonda).
Il lavoro manuale eseguito sul sistema aperto è rappresentato dall’area racchiusa dal cammino complessivo 1-2-3-4-1 (vedi l’area tratteggiata in fig.5b ):
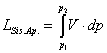
Si noti che durante la fase di spinta (1-2-3) il sistema ha richiesto lavoro dall’ambiente, in quella di recupero (4-1) l’ha riceduto, di modo che il lavoro netto dell’ambiente è stato nullo;quindi non c’è stato bisogno di sottrarlo come al punto a).
Infine, il percorso eseguito, si dice ciclo chiuso: partendo dal punto 1, attraverso varie trasformazioni vi siamo tornati.
Per quanto detto precedentemente il sistema è aperto; quindi, dato il ciclo chiuso effettuato, ed essendo l’entalpia una funzione di stato (non dipende dal cammino), la variazione della stessa è nulla DH = 0.
Esercizio n°5.
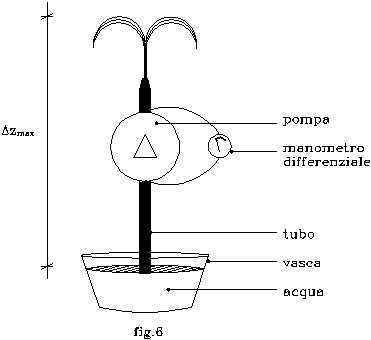
Sia data una vasca contenente acqua ( fig.6 ).
Un tubo disposto verticalmente attinga dalla stessa tramite una pompa avente una prevalenza Dp = 3 bar .
Questo salto di pressione venga misurato ai capi della pompa mediante un barometro differenziale.
Considerando che il tubo termini con un beccuccio da cui fuoriesce l’acqua, determinare spannometricamente la massima altezza Dzmax che può raggiungere lo zampillo rispetto al pelo libero della vasca.
Soluzione esercizio n°5.
L’acqua ha un peso specifico pari a rAcq.= 1000 kg/m3 mentre il mercurio rHg=13596 kg/m3 ( tab.2 ) , cioè 13.6 volte minore del secondo.
Per ottenere la stessa pressione che esercita una colonna di 760 mmHg (dall’esperienza di Torricelli), la colonna d’acqua dovrà avere un’altezza pari a:
![]() .
(35)
.
(35)
Da cui, se la prevalenza della pompa vale 3 bar, l’acqua riuscirà a raggiungere una quota 3 volte superiore che in presenza della sola atmosfera (pAtm. = 1 bar):
![]() .
(36)
.
(36)
Esercizio n°6.
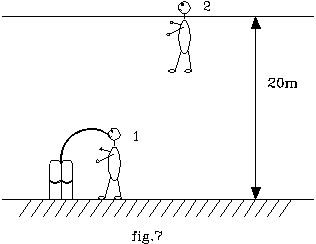
Si consideri un subacqueo zavorrato sul fondo del mare ad una profondità di 20m .
La sua capacità polmonare sia di V1 = 6l .
Dopo aver inspirato tale volume d’aria dalla bombola, egli risalga in superficie levando le zavorre che lo tengono ancorato.
Si assuma, inoltre, che la pressione dell’aria uscente dall’erogatore (p1)sia pari a quella dell’ambiente in cui si trova.
Determinare il volume dell’aria nei polmoni (V2) del sub risalito a galla e il valore della forza di galleggiamento dello stesso.
Soluzione esercizio n°6.
Conformiamo le unità di misura dei dati a quelle del SI ( tab.5 ):
![]() ,
,
![]() .
.
La pressione con cui l’aria esce dal respiratore è pari a quella presente nell’ambiente 1; essa è data dalla somma fra la pressione atmosferica e quella dovuta alla ipotetica colonna d’acqua di 20m .
Viste le considerazioni fatte nell’esercizio precedente (una colonna d’acqua alta 10.3m esercita una pressione di 1 bar), la pressione dovuta all’acqua è circa di 2 bar, perciò:
![]() .
(37)
.
(37)
Supponendo che la temperatura corporea rimanga costante, possiamo considerare i polmoni del sub un sistema chiuso in cui avviene una trasformazione isotermica:
![]() ,
(38)
,
(38)
![]() , (39)
, (39)
e il volume in 2 sarà:
![]() .
(40)
.
(40)
Dato che il peso specifico dell’acqua è rAcq.= 1000 kg/m3 ( tab.2 ) e dato che la forza di galleggiamento è pari al peso del liquido spostato (Archimede), si ha:
![]() . (41)
. (41)
Naturalmente il sub muore per l’eccessivo aumento di volume dei suoi polmoni.
Esercizio n°7.
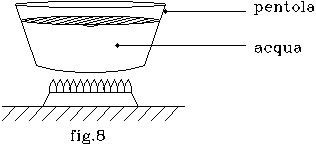
Sia data una pentola contenente 10 lb di acqua ( fig.8 ).
Venga messa sul fuoco aumentando la temperatura dell’acqua da 0°R a 80°R e da 32°F a 212°F.
Determinare la quantità di calore necessaria per operare il riscaldamento nei due casi.
Soluzione esercizio n°7.
Osservando le tabelle di conversione ( tab.3, tab.4, tab.6 ) si ha che:
a)
0°R =
0°C
b)
80°R =
100°C
c)
32°F =
0°C
d)
212°F
= 100°C
e)
10lb
(GB) = 4356g
f)
1 cal
= 4.186 J
Quindi l’acqua subisce in ogni caso un salto di temperatura che và dal congelamento all’ebollizione (DT = 100°C).
La caloria è la quantità di calore necessaria per innalzare di 1°C la temperatura di 1g d’acqua (14.5°C – 15.5°C) alla pressione atmosferica.
Perciò il calore necessario per la trasformazione è lo stesso in entrambe i casi e vale:
![]() ,
(42)
,
(42)
![]() . (43)
. (43)
Tabelle relative agli
esercizi proposti.
tab.1
Potenza
|
W
|
Kpm/s
|
CV
|
HP
|
|
W |
1 |
0.102 |
1.36 ×10-3 |
1.34 ×10-3 |
Kpm/s
|
9.80 |
1 |
0.01333 |
0.01315 |
CV
|
736 |
75 |
1 |
0.986 |
|
HP |
745.2 |
76.04 |
1.014 |
1 |
legenda:
W :
Watt ,
Kpm/s : kilogrammetro al secondo
, CV : cavallo-vapore , HP
: horse-power
tab.2
Pesi
specifici di alcuni solidi e liquidi ( kg/m3 )
|
Acciaio 7.86 |
Gomma lavorata 1-2 |
|
Acqua distillata 1 |
Graffite 1.9-2.3 |
|
Acqua di mare 1.02-1.03 |
Granito 2.3-2.6 |
|
Alabastro 2.3-2.8 |
Linoleum 1.2 |
|
Alcool etilico 0.8 |
Malta 1.8 |
|
Alluminio 2.7 |
Marmo 2.7-2.8 |
|
Ambra 1 |
Mattoni 1.4-1.8 |
|
Amianto 2.1-2.8 |
Mercurio 13.596 |
|
Arenaria 1.8-2.5 |
Mica 2.6-3.2 |
|
Argento 10.49 |
Nafta 0.75-0.77 |
|
Argilla 2-2.5 |
Neve 0.080-0.19 |
|
Avorio 1.9 |
Nichel 8.8 |
|
Bachelite 1.3 |
Oli vegetali 0.91-0.93 |
|
Basalto 2.7-3.2 |
Oro 19.3 |
|
Benzina 0.68-0.7 |
Ottone 8.4-8.6 |
|
Bitume 1.5 |
Paraffina 0.9 |
|
Bronzo 7.4-8.8 |
Petrolio 0.79-0.82 |
|
Burro 0.95 |
Piombo 11.34 |
|
Calcare compatto 2.4-2.8 |
Pirite 4.9-5.2 |
|
Calcestruzzo 2 |
Platino 21.4 |
|
Caolino 2.1-2.3 |
Pomice 0.4-0.9 |
|
Carbone fossile 0.72-0.85 |
Porcellana 2.4 |
|
Carta 0.7-1.1 |
Quarzo 2.6 |
|
Catrame 1.2 |
Rame 8.93 |
|
Celluloide 1.4 |
Sabbia in mucchio 1.6 |
|
Cellulosa 1.5 |
Sale da cucina 2.15 |
|
Cemento 1.4 |
Salgemma 2.2 |
|
Cera 0.95 |
Sego 0.95 |
|
Cromo 7.14 |
Serpentino 2.5-2.7 |
|
Cuoio ingrassato 1.05 |
Silice 1.8-2 |
|
Dinamite 1.5 |
Stagno 7.28 |
|
Ebanite 1.15 |
Sughero 0.2-0.35 |
|
Eternit 2 |
Talco 2.6-2.8 |
|
Ferro 7.86 |
Travertino 2.2-2.5 |
|
Fibra vulcanizzata 1.1-1.45 |
Tufo 1.1-1.9 |
|
Ghiaccio 0.9 |
Tungsteno 19.1 |
|
Ghisa in getti 7.25 |
Zinco 7.1 |
|
Gomma elastica 0.92 |
Zolfo 2 |
tab.3
Relazioni fra scale di temperatura
|
T(K) = T(°C) + 273.15 = 5/9 T(°F) + 255.37 = 5/4 T(°R) +273.15 |
|
T(°C) = T(K) – 273.15 = 5/9 [T(°F) – 32] = 5/4 T(°R) |
|
T(°F) = 9/5 [T(K) – 255.37] = 9/5 T(°C) +32 = 9/4 T(°R) +32 |
|
T(°R) = 4/5 [T(K) – 273.15] = 4/5 T(°C) = 4/9 [T(°F) –32] |
Relazioni intuitive
|
Congelamento dell’acqua |
Ebollizione dell’acqua |
|
K |
273.15 |
373.15 |
|
°C |
0 |
100 |
|
°F |
32 |
212 |
|
°R |
0 |
80 |
legenda:
K :
Kelvin o scala di Temperatura Assoluta
°C : Grado Celsius o Centigrado
°F : Grado Fahrenheit (grado britannico o statunitense)
°R : Grado Réamur o Ottantigrado (grado tedesco)
tab.4
Energia
|
J
|
erg |
cal |
eV |
J
|
1 |
107 |
0.239 |
6.24×1018 |
erg
|
10-7 |
1 |
2.39×10-8 |
6.24×1011 |
cal
|
4.184 |
4.184×107 |
1 |
2.61×1019 |
|
eV |
1.602×10-19 |
1.602×10-12 |
3.83×10-20 |
1 |
legenda:
J :
Joule , erg : Erg , cal : caloria , eV : elettronvolt
tab.5
Pressione
|
Pa
|
atm |
bar |
torr (mmHg) |
mH2O |
kp/cm2 |
Pa
|
1 |
9.869×10-6 |
10-5 |
7.5×10-3 |
1.019×10-4 |
1.019×10-5 |
atm
|
1.013×105 |
1 |
1.013 |
763.3 |
10.33 |
1.033 |
bar
|
105 |
0.9869 |
1 |
750 |
10.2 |
1.02 |
|
torr (mmHg) |
1.333×102 |
1.31×10-3 |
1.333×10-3 |
1 |
0.0135 |
0.00135 |
|
mH2O |
9.81×103 |
0.0968 |
0.098 |
73.5 |
1 |
0.1 |
|
kp/cm2 |
9.81×104 |
0.968 |
0.98 |
735.7 |
10 |
1 |
legenda:
Pa :
Pascal(N/m2) , atm : atmosfera , torr : Torricelli o
millimetri di mercurio ,
mH2O : metri d’acqua
, kp/cm2 :
chilogrammosucentimetroquadrato
tab.6
Relazione
fra scale di peso
|
1 lb(USA)
=0.453600 kg |
|
1 lb(GB) =
0.435600 kg |
tab.7
Calore specifico di alcune sostanze a temperatura ambiente
(T = 298 K) e a pressione atmosferica
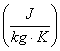
|
Acqua 4186.0 |
Idrogeno 14985.9 |
|
Alluminio 962.8 |
Mercurio 138.1 |
|
Anidride carbonica 837.2 |
Oro 134.0 |
|
Argento 238.6 |
Ossigeno 920.9 |
|
Aria 1004.6 |
Ottone 376.7 |
|
Carbonio 506.5 |
Rame 389.3 |
|
Elio 5232.5 |
Vapore d’acqua 2009.3 |
|
Ferro 481.4 |
Vetro (in media) 837.2 |