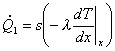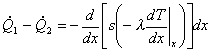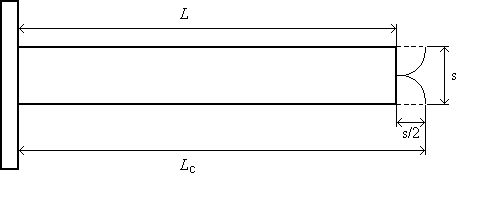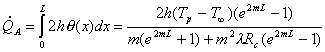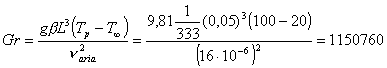Superfici Alettate

Cosa sono le alette

Le alette sono particolari componenti che servono per aumentare lo scambio termico tra un dispositivo e l’ambiente e dunque a migliorare il raffreddamento del dispositivo stesso.

Possono essere ricavate direttamente sul corpo del dispositivo per fusione, in fase di costruzione, oppure essere realizzate a parte e poi essere applicate in un secondo tempo.

Fig.1 – Dispositivo munito di alette.

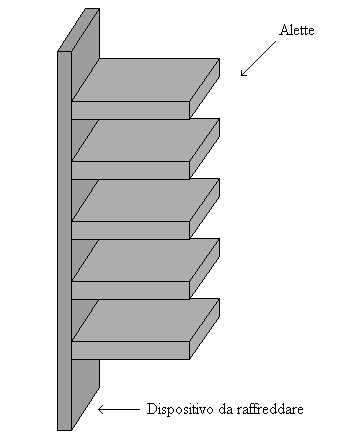
Le alette possono avere svariate forme che permettono loro di migliorare le prestazioni. Esistono alette diritte, coniche, a spillo, circolari e molte altre; quelle qui presentate sono quelle diritte, che sono anche le più semplici da studiare.

Lo studio di una aletta avviene tramite due parametri geometrici: la lunghezza L e lo spessore s. Per quanto riguarda la larghezza possiamo supporla infinita o unitaria.

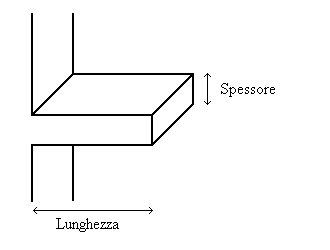
Fig.2 – Aletta diritta.

Come funzionano

Il calore fluisce per conduzione nel metallo, dal dispositivo attraverso le alette e poi viene disperso per convezione sulle facce

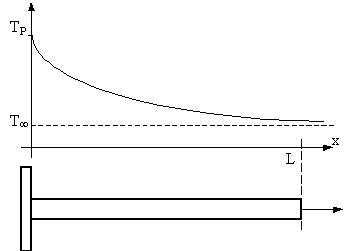
Lo scambio termico, però, non è proporzionale alla superficie dell’aletta in quanto la temperatura di questa varia lungo di essa. Nel caso in cui l’aletta sia stata ottenuta per fusione dal dispositivo, nel punto di contatto entrambi avranno la stessa temperatura che indicheremo con T_P (temperatura di parete). Spostandoci lungo l’aletta, la temperatura tenderà a diminuire fino al valore di temperatura dell’ambiente circostante (normalmente rappresentato dall’aria) che indicheremo con T_.

Fig.3 – Temperatura di una aletta ottenuta per fusione, in funzione della sua lunghezza.

Nel caso in cui, invece, l’aletta sia stata applicata successivamente, bisognerà tenere conto di una certa resistenza R_C nel punto di contatto col dispositivo. In tal caso la temperatura alla base dell’aletta sarà inferiore a T_P .

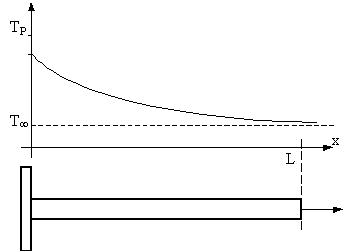
Fig.4 – Temperatura di una aletta applicata successivamente ad un dispositivo, in funzione della sua lunghezza.

Osservando le figure 3 e 4 si nota che esiste una lunghezza ottimale per le alette oltre la quale lo scambio di calore è pressoché nullo essendo la temperatura dell’aletta di poco superiore a quella dell’ambiente, cioè T.

Vediamo ora di studiare il funzionamento delle alette dal punto di vista matematico. Prima di tutto facciamo un’ipotesi semplificativa: supponiamo che la propagazione del calore per conduzione nell’aletta avvenga solo lungo la componete parallela ad essa.

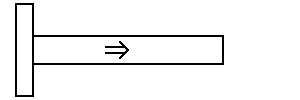
Fig.5 – Verso di propagazione del calore nell’aletta.

In realtà il calore si propaga anche dal centro verso le superfici esterne dell’aletta ma se lo spessore è trascurabile rispetto alla lunghezza (s<<L) l’ipotesi fatta risulta accettabile.

Vediamo ora il calcolo.

Prendiamo un elemento infinitesimo dell’aletta e valutiamo il calore scambiato.

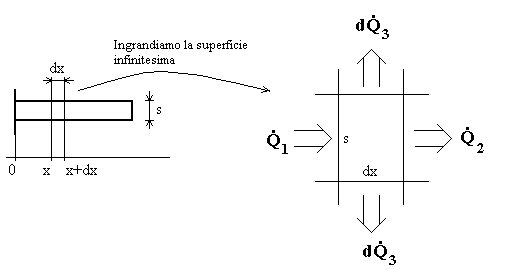
Fig.6 – Analisi di un elemento infinitesimo.

e rappresentano le potenze scambiate per conduzione, mentre rappresenta la potenza scambiata per convezione. Supponiamo che quest’ultima assuma lo stesso valore sia relativamente alla superficie superiore che a quella inferiore.

Bilanciando gli scambi abbiamo che:

Potenza entrante = Potenza uscente (1)

ovvero

(2)

ma anche:

(3)

La potenza di conduzione si calcola tramite la Legge di Fourier:

(4)

dove l è la conducibilità termica del materiale di cui è fatta l’aletta.

Per il calore entrante nell’elemento nel punto x, dunque, otteniamo:

(5)

mentre per il calore uscente dall’elemento nel punto x+dx possiamo utilizzare uno sviluppo di Taylor:

(6)

da cui otteniamo:

(7)

Sostituendo la (5) nel secondo membro della (7) otteniamo:

(8)

ovvero

(9)

Per quanto riguarda la potenza scambiata per convezione, abbiamo:

(10)

dove h è il coefficiente di convezione.

Sostituendo, dunque, la (9) e la (10) nella (3) otteniamo:

(11)

ovvero, ponendo :

(12)

che è un’equazione differenziale omogenea di secondo grado.

Poniamo ora e otteniamo:

(13)

analoga all’equazione di D’Alembert vista in acustica.

La soluzione, dunque, risulta:

(14)

Nell’acustica m² era negativo e quindi m era immaginario; questo, secondo le equazioni di Eulero, portava ad avere una funzione q oscillante.

In questo caso invece m² è positivo e dunque q rappresenta una funzione smorzata.

Non ci resta che risolvere l’equazione (13). Per farlo dovremo procedere ad un’integrazione. Vediamo dunque di valutare le condizioni al contorno, vale a dire per x=0 e per x=L.

Per x=0 imponiamo il valore della temperatura alla base dell’aletta. Per farlo dobbiamo tenere conto che il dispositivo si trova alla temperatura T_P e che fra esso e la base dell’aletta esiste una resistenza R_c.

Per x=L impongo il valore del flusso di convezione. Supponiamo, infatti, che la punta dell’aletta non scambi calore per convezione con l’ambiente, ovvero . Se s<<L ciò è più che accettabile ma esistono anche alette il cui spessore è paragonabile alla lunghezza. Tali alette si dicono “tozze”. In tal caso si procede in questo modo: si considera un’aletta equivalente di lunghezza L_c=L+(s/2) e si suppone che non scambi calore tramite la punta. In questo caso, infatti, la perdita di calore per convezione avviene solo tramite le pareti ma equivale alla perdita della aletta originaria.

Procedendo in questo modo è come se avessimo spaccato la punta dell’aletta e l’avessimo aperta in modo da prolungare la sua superficie.

Fig.7 – Metodo grafico per il calcolo della lunghezza corretta L_c.

Le condizioni al contorno, dunque, diventano:

(15)

(16)

dove e .

Risolvendo, troviamo l’espressione (14) con:

(17)

(18)

Sostituendo (17) e (18) nella (14) otteniamo:

(19)

dove si vede che m, costante di estinzione dell’onda, è dimensionalmente l’inverso di una lunghezza essendo l’esponenziale ad esponente adimensionale.

Calcoliamo, ora, la potenza scambiata per convezione dall’aletta:

(20)

Notiamo che se l’aletta fosse stata ricavata dal dispositivo per fusione avremmo avuto R_c = 0 e il risultato si sarebbe notevolmente semplificato.

Efficienza dell’aletta

La potenza scambiata dall’aletta è inferiore a quella scambiata se l’aletta fosse isoterma. Vediamolo meglio introducendo l’efficienza dell’aletta:

(21)

dove 2hL(T_P – T_¥) rappresenta la potenza che l’aletta scambierebbe se fosse tutta alla medesima temperatura.

Sostituendo (20) in (21) otteniamo:

(22)

Al crescere della lunghezza L () l’efficienza diminuisce sempre più () mentre la potenza tende ad un valore massimo.

Migliore è la conducibilità l, invece, migliore risulta essere il funzionamento (ad esempio utilizzando alluminio).

Bisogna dunque bilanciare L e l. In genere le alette non hanno mai un’efficienza inferiore al 40%.

Efficienza dell’alettatura

Cerchiamo, ora, di valutare l’efficienza di una alettatura, ovvero di un insieme di alette.

Fig.8 – Rappresentazione di un’alettatura.

Chiamiamo S₀ la superficie da raffreddare, S_al la superficie del dispositivo ricoperta di alette, S_piana la superficie del dispositivo in contatto diretto con l’ambiente e S_svil la superficie dell’alettatura a contatto dell’aria.

Abbiamo che S₀ = S_al + S_piana.

La superficie non alettata del dispositivo S_piana scambia calore direttamente da T_P a T_¥: per questo processo prendiamo efficienza e = 1.

Valutiamo la potenza scambiata:

(23)

dove al secondo membro abbiamo rispettivamente la potenza scambiata dalle alette e quella scambiata dalla superficie non alettata.

Consideriamo l’alettatura come una singola aletta e sviluppiamo la (23):

(24)

dove nel secondo addendo del secondo membro non compare l’efficienza che avevamo precedentemente posto unitaria.

Il tutto si può riscrivere come:

dove S_al,tot = S_piana + S_svil ovvero l’intera superficie a contatto con l’aria, mentre e_al,tot risulta essere l’efficienza dell’alettatura che tiene conto sia delle alette che della superficie non alettata.

Riportiamo di seguito due grafici molto importanti riguardo l’efficienza.

Fig.9 – Efficienze comparate di un’aletta rettangolare ed una triangolare.

Fig.10 – Efficienze comparate di alette circolari e diritte.

Esercizio

Una CPU di superficie quadrata (L=50mm) dissipa una potenza di 20w nell’ambiente (avente temperatura pari 20°C).

· trovare a che temperatura si porta.

· progettare un’opportuna alettatura per abbassarne la temperatura.

I 20w dissipati rappresentano i watt elettrici assorbiti nel funzionamento. La CPU dissipa tutto in calore.

Risolviamo il problema in convezione naturale, ovvero l’ambiente è rappresentato dall’aria ferma. Questo caso risulta un po’ più difficile rispetto alla convezione forzata che si ha, ad esempio, con l’impiego di una ventola.

La dissipazione del calore da parte della CPU avviene solo da un lato (in questo caso dal destro) poiché dall’altro si trova la Mainboard.

Consideriamo innanzitutto il problema senza alettatura.

Fig.11 – CPU priva di alettatura.

La potenza scambiata sarà:

da cui:

Supponiamo di considerare accettabile per la CPU una temperatura di 100°C.

Calcoliamo dunque il numero di Grashof Gr:

g=9.81m/s² è l’accelerazione di gravità

b=1/T è il coefficiente di dilatazione termica (che nel caso di gas è l'inverso della temperatura).

L=0.05m è il lato della superficie quadrata

n_aria=16^.10^-6m²/s è la viscosità cinematica dell’aria

Il numero di Prandtl in queste condizioni è Pr=0,71

Possiamo, dunque, calcolare il numero di Rayleigh Ra:

che come si vede è <<, il che significa che ci troviamo di fronte ad un moto laminare.

Valutiamo, ora, il numero di Nusselt:

ma anche:

con l_aria=0,03w/mK conducibilità termica dell’aria.

Ricaviamo, dunque, h:

Possiamo calcolare la temperatura del dispositivo:

decisamente troppo alta!

Nella trattazione precedente, però, è stato trascurato lo scambio termico dovuto all’irraggiamento. Ripetiamo il procedimento considerandolo.

Al posto di h prenderò h_tot=h+h_r,dove h_r è il coefficiente di irraggiamento:

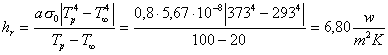
dove a=0,8 è il coefficiente di assorbimento del materiale, in genere plastica nera, e s₀=5,67·10^-8 w/m²K⁴ è la costante di Stefan-Boltzmann

Per cui

Il che ci porta a calcolare comunque troppa alta!

Non v’è dubbio che serva un’alettatura.

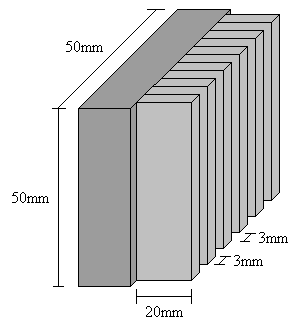
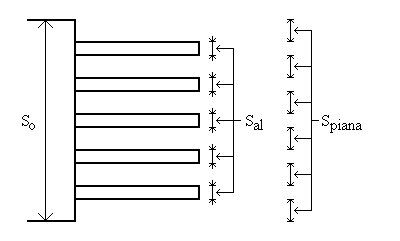
Fig.12 – CPU munita di alettatura.

Consideriamo un’alettatura in alluminio (l_all=206w/mK) ricavata per fusione (R_c=0). Ogni aletta ha lunghezza L=20mm, larghezza pari al dispositivo, spessore s=3mm e dista dalla successiva 3mm. Da ciò si deduce che il numero massimo di alette applicabili sarà 8.

Rifacendoci alla teoria abbiamo:

ma anche:

dove:

Inoltre:

da cui notiamo che lo sviluppo completo delle alette è decisamente maggiore dell’area della CPU.

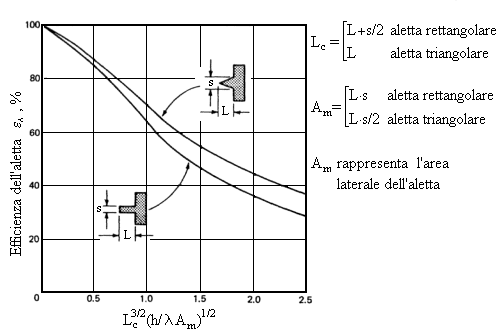
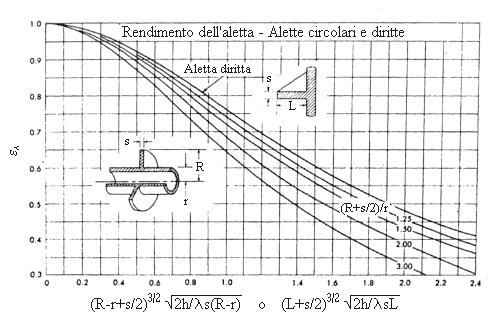
Calcoliamo inoltre:

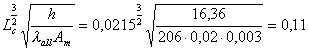
conoscendo il quale possiamo ricavare l’efficienza sul diagramma di Fig.9 che risulta e_A=0,93.

Inoltre, conoscendo:

ricaviamo la temperatura:

che è un valore accettabile.

In questi caso, come nei precedenti quando non utilizzavamo l’alettatura, dopo aver trovato la temperatura dovrei ricalcolare i coefficienti per i quali avevamo scelto la temperatura di 100°C. In tal modo troverei una temperatura leggermente diversa ma più vicina a quella reale. Se poi iterassimo il procedimento ricalcolando nuovamente i coefficienti e poi la temperatura più volte, troveremmo la temperatura esatta.

Potevo inoltre migliorare le prestazioni allungando le alette o aumentare il coefficiente di convezione applicando una ventola (in convezione forzata il coefficiente di convezione risulterebbe 30 – 35 volte superiore). Così facendo avremmo aumentato la dissipazione e diminuito la temperatura.