Facoltà di Ingegneria

Corso di Laurea in Elettronica

 

 

 

 

anno accademico 2000/2001

corso di Fisica Tecnica

docente : Prof. Ing. Angelo FARINA

 

Relazione su : “Onde piane stazionarie e onde sferiche”

inerente la Parte n°3 del corso, ovvero “Acustica ed Elettroacustica”

svolta nella lezione del 14/11/2000 nelle ore 16.30 - 18.30

 

Redattore : Mario MOLES (matr. N°135678)

 

Sommario degli argomenti :

 

¨    Onde piane e definizione di Impedenza acustica (Tubo di Kundt)

¨    Definizione ed analisi del fenomeno delle Onde stazionarie

¨    Calcolo del Coefficiente di assorbimento

¨    Calcolo dell’impedenza (modulo e fase)

¨    Definizione ed analisi delle Onde Sferiche

¨    Analisi energetica

¨    Effetto di prossimità

¨    Analisi intensimetrica

 

 

 

 

nota : per una corretta visualizzazione dei disegni è necessario passare dalla visualizzazione NORMALE a quella LAYOUT DI PAGINA.

Onde piane - definizione di Impedenza acustica

 

Spesso, nell’impiego di svariati materiali, è utile, se non necessario, conoscerne le proprietà acustiche quali il coefficiente di assorbimento  e l’impedenza Z, sì da privilegiare l’impiego di un tipo specifico all’uso che si richiede. A tal fine è d’abitudine avvalersi di uno strumento misuratore, che possa testare un campione di grandezza significativa. Questo è lo scopo del cosiddetto “tubo di Kundt”, illustrato qui di seguito :

 

 

   a)

 

 

 

 

   b)

 

 

 

 

   c)

   d)

 

 

 

 

 e)

 

 

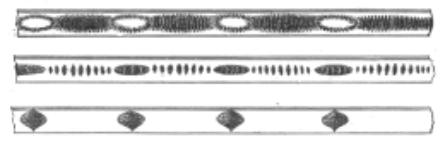
Fig.1 - Tubo di Kundt

 

Le figure qui di sopra mostrano un modello di Tubo di Kundt da laboratorio (figg.a, b, d) ed un suo spaccato (fig.c), mentre l’ultima un modello, di dimensioni considerevoli, utilizzato per prove su scala industriale.

 Esso è costituito da un cilindro sigillato alla cui estremità è alloggiato un altoparlante. Quest’ultimo genera una serie di onde piane (cioè dirette lungo un solo asse spaziale) che vanno ad investire il campione da testare posto nel fondo, come fosse una sorta di tappo, all’altra estremità del cilindro. Le onde generate dall’altoparlante giungono perpendicolari al campione, con una certa pressione P ed una velocità u istantanee. Dalla formula riportata qui di seguito è immediato  il calcolo dell’impedenza equivalente. Data la frequente sfasatura tra P ed u, essa è spesso una grandezza complessa :

 

                                                                                                      (1)  

 

Perché la misura presenti la maggiore accuratezza possibile è necessario che il tubo presenti accorgimenti costruttivi, ad esempio un’estensione decisamente maggiore della lunghezza d’onda stabilita per il suono di prova emesso dall’altoparlante. Infatti, in tal maniera, è possibile che il campione venga investito da un’onda per così dire “pulita e completa”, che non risente della vicinanza alla sorgente sonora. Dunque si ragiona sempre in termini di. Per procedere con la misurazione, è conveniente fissare un sistema di riferimento cartesiano, destrorso, ideale, con origine nel centro del campione, sulla faccia rivolta all’altoparlante. Ora un suono di prova con specifiche pressione e lunghezza d’onda può bersagliare il campione che, a sua volta, reagirà assorbendone una certa quantità e riflettendone un’altra. In seguito entreremo meglio nello specifico.

 

Nascita delle onde stazionarie

 

Nel processo sperimentale a cui si faceva cenno poc’anzi è di considerevole importanza l’insorgere di fenomeni aggiuntivi, quali quello delle “Onde stazionarie”. Esse sono il prodotto della sovrapposizione di due distinti fenomeni ondulatori : il primo generato dall’altoparlante (il suono di prova), il secondo generato dal materiale (suono riflesso). Infatti, l’onda in arrivo sul campione non ha “strada libera” innanzi a sé, ma deve scontrarsi con quella porzione che viene riflessa dal materiale. Ne consegue una nota matematica : per tener conto di tale effetto, in materia di equazione di D’Alambert, dobbiamo considerare l’espressione del potenziale della velocità  come la sommatoria di due distinte componenti, una positiva, l’altra negativa,  rispettivamente appartenenti all’onda diretta la prima e all’onda riflessa la seconda. Pertanto, omettendo passaggi algebrici intermedi, l’espressione diviene:

 

                                                                            (2)

 

ove appunto il pedice + e quello - indicano il potenziale lungo la direzione positiva e negativa rispettivamente.

 

Calcolo del coefficiente di assorbimento

 

Per giungere al calcolo del coefficiente d’assorbimento del materiale in esame premettiamo alcune considerazioni : innanzitutto, come avviene per la maggior parte di questi fenomeni fisici, possiamo considerare valido il principio di sovrapposizione degli effetti. Difatti è possibile calcolare separatamente le intensità dell’onda incidente e di quella riflessa, come se l’altra delle due non fosse presente. L’intensità totale è dunque semplicemente la somma di quelle componenti. Nel caso specifico avviene questo : l’onda sonora investe il campione di materiale, poi mentre una parte di essa viene assorbita dallo stesso, la rimanente torna “sui propri passi”. In formule abbiamo :

 

                                                                                (3)

 

Poi, dividendo la (3) membro a membro per l’intensità incidente, otteniamo due nuove grandezze : il coefficiente di riflessione r e quello di assorbimento.

 

                                                    (4)

 

Infine esplicitiamo  con semplici passaggi algebrici ponendo la (4) come :

 

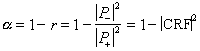                                                                      (5)

 

in cui ci siamo avvalsi del rapporto tra la pressione dell’onda riflessa e quella incidente, denominato appunto CRF (ovvero Rapporto complesso di riflessione), oltre che della relazione che lega l’intensità I alla pressione P, come espressione del modulo quadro di quest’ultima.

Adesso non dobbiamo fare altro che misurare i moduli delle due pressioni per risalire direttamente al coefficiente ricercato. Quest’operazione, però, non è del tutto banale. Infatti, per quanto discusso prima, è vera la possibilità di considerare separatamente le varie componenti ondulatorie, ma è altresì vero che in natura tale distinzione è del tutto ideale. Come sempre, giunge in soccorso di tale necessità uno strumento appositamente creato : esso è un microfono molto particolare. Viene inserito nel cilindro in questione attraverso un foro sulla faccia del provino e ancorato ad un’asta di dimensioni minime, che a sua volta è saldata ad un carrello esterno al cilindro. Questo sistema permette all’apparato asta-microfono di scorrere lungo tutta la parte interna del cilindro stesso. Così facendo è possibile misurare i valori di pressione presenti in ogni punto appartenente all’asse geometrico del cilindro. Ne risulta il grafico sottostante :

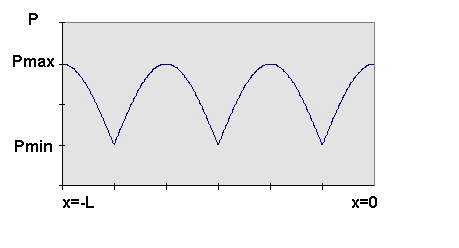
Fig.2 - grafico andamento pressione acustica nel Tubo di Kundt

 

in cui la coordinata x=-L rappresenta la posizione dell’altoparlante e quella x=0 la posizione del campione di materiale da testare.

 

Facciamo ora alcune significative considerazioni che scaturiscono da questo rilevamento : innanzitutto notiamo che la pressione dell’onda acustica fluttua in modo del tutto regolare, tra un valore minimo ed uno massimo, e che quest’ultimo è assunto precisamente anche all’origine del sistema (sulla faccia del provino) e nella coordinata x=-L (ovvero nel punto in cui è situato l’altoparlante, la sorgente del suono). Il fatto che la pressione non mantenga un livello costante è dovuto alla sola sfasatura tra le sue due principali componenti : infatti, per norma del tutto generale, quando due onde s’incontrano se esse sono in fase i loro moduli si sommano, altrimenti in opposizione si sottraggono. L’onda risultante fluttua perciò tra un valore massimo (onde in fase) ed uno minimo (onde in opposizione di fase). Algebricamente si può scrivere così :

 

                                                                                                (6)

 

Questo sistema rappresenta il legame tra i valori di picco delle pressioni e le due componenti principali. Dalla sua risoluzione otteniamo :

 

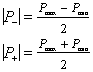                                                                                                                        (7)

 

che rappresentano proprio i valori ricercati. Ricordiamo ancora una volta che dalla (5), mediante l’espressione del CRF, scaturisce l’espressione finale del coefficiente di assorbimento :

 

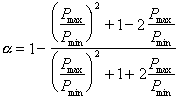                                                                           (8)

 

Il grafico alla pagina seguente mostra il coefficiente  in funzione del rapporto tra la pressione massima e quella minima rilevate, denominato n :

 

 

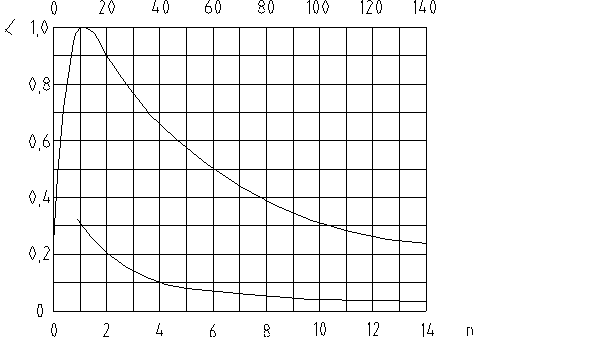
Fig.3 - Grafico dell’andamento del C.d.A. in funzione delle pressioni acustiche

 

Attenzione però alla consultazione del grafico in Fig.3 ! Esso va letto così : la curva superiore deve essere riferita in funzione della scala superiore, quella inferiore viceversa.

Ad una conclusione analoga, sebbene più esaustiva rispetto a quella appena raggiunta, si giunge mediante la soluzione della nota equazione d’onda. Essa però è di difficile accesso, per causa di lungaggini matematiche insite nei calcoli connessi, eppure porta alla conoscenza ulteriore di tutti i valori di pressione compresi tra quelli di picco.

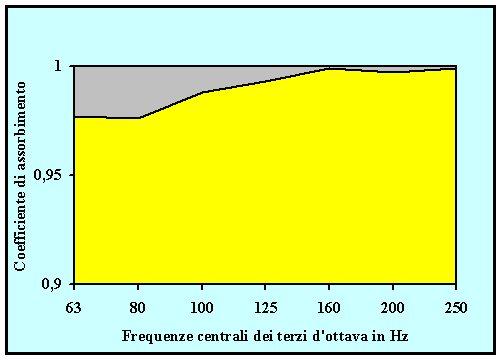
Fig.4 - Grafico-esempio dell’andamento del C.d.A. in una prova

Calcolo dell’impedenza acustica

 

Da quanto analizzato nelle lezioni precedenti e direttamente dalla (1) discende l’espressione :

 

                                                (9)

 

La relazione (9) sovrastante mostra come i dati finora acquisiti permettano un calcolo diretto dell’impedenza superficiale (in modulo) del campione in esame. Il calcolo della fase non è così diretto e al solito passa per l’equazione d’onda :

 

                                                             (10)

 

in cui la fase è rappresentata di consueto dal termine  all’esponente.

Citiamo un esempio chiarificatore, che è anche un metodo più rapido per determinare l’impedenza : nella prova di un materiale a caso, supponiamo che esso ne sia caratterizzato da una di misura reale, proprio nell’origine del sistema, ovvero sulla superficie del campione stesso. Per quanto discusso prima qui ha luogo un massimo nell’espressione delle pressioni acustiche. Ritroviamo un minimo appena prima, retrocedendo lungo la coordinata longitudinale : avevamo concluso che ciò implica che le due onde, e i loro rispettivi fasori rappresentativi  ed , si trovano in opposizione di fase, ovvero hanno ruotato rispettivamente di 90° cadauna, formando tra loro un angolo piatto. Ciò accade proprio ad una distanza di  dall’origine del sistema di riferimento. Cambiando materiale e supponendo al contrario che, all’origine del sistema, questo abbia le due componenti già sfasate, noteremo che il punto di minimo di cui sopra si sarà spostato in un intorno della posizione x=-. Tutto ciò riconduce ad un’equivalenza di tutti i materiali a meno di una costante spaziale, propria di ogni mezzo, che ne identifica il punto di riflessione. In altre parole è come se il materiale “sfasato” presenti una superficie di riflessione virtuale spostata della stessa costante spaziale prima citata più al suo interno o al di fuori di esso. Il grafico seguente è utile alla comprensione di quanto avviene in un materiale con impedenza reale :

 

                             P

                     Pmax

 

 


                     Pmin

                 -x

                                                     

 

Fig.5 - grafico dell’andamento della Pressione in un materiale con impedenza superficiale reale.

 

 

Fig.6 - Grafico dell’andamento della fase nelle due onde dell’esperimento nel Tubo di Kundt

 

Da ciò scaturisce un metodo ancora più diretto di quello del calcolo della pressione per ricavare la fase : occorre semplicemente conoscere la posizione del primo minimo e confrontarla con la distanza dalla superficie del campione. In formule abbiamo :

 

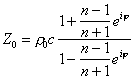                                                                                (11)

 

in cui :                                                                                          (12)

 

e la fase all’esponente risulta essere :

 

                                                                                      (13)

ove per  s’intende la distanza dell’ultimo minimo dal provino.

Onde sferiche

 

Si definiscono Onde sferiche quelle prodotte da una sorgente di forma sferica che immaginiamo variare il proprio volume, dilatandosi e riducendosi rispetto alla posizione di quiete, in maniera uniforme per ogni punto della superficie. Tale moto oscillatorio lungo le tre coordinate spaziali, paragonabile ad un palloncino che si gonfia e si sgonfia ciclicamente, fa sì che ciascun punto dello spazio, equidistante dalla superficie sferica in esame, venga perturbato nello stesso modo. Ciò significa medesima velocità di propagazione per l’onda generata, qualunque ne sia la direzione considerata.

Per avere un’idea di quanto detto si veda l’illustrazione seguente :

 

 


                             

                                            r

 

 

 

 


Fig.7 - rappresentazione di una sorgente di onde sferiche

 

Per l’analisi di tale fenomeno è opportuno considerare l’equazione di D’Alambert espressa in coordinate sferiche. Essa diviene pertanto :

 

                                                                                                           (14)

 

la cui soluzione è rappresentata da :

 

                                                                                                                         (15)

 

Calcoliamo allora la velocità di un generico punto, posto a distanza r dal centro della sfera. Essa è ricavabile, com’è noto, svolgendo il gradiente della soluzione appena ricavata, (in analogia al moto monodimensionale, effettuare il gradiente appena calcolato è come derivare rispetto al tempo la coordinata x di un punto in movimento lungo un asse cartesiano, ovvero ricavarne la velocità istantanea, solo che, nel caso della (16), la derivata è calcolata nelle tre dimensioni spaziali). Si ottiene pertanto :

                           

                                                                     (16)

 

Considerando che la parete sferica e l’aria (il mezzo circostante) sono a contatto, è giusto assumere che i loro due moti siano interdipendenti. Si ha pertanto :

 

                                                                                                      (17)

 

                                                                                    (18)

 

Detto ciò, esplicitiamo come :

 

                                                                            (19)

 

Sostituendo la (19) appena ottenuta nella (16) ricaviamo la velocità u in funzione di r e :

 

                                                                  (20)

 

Ora, mediante l’Equazione di Eulero :

 

                                                                             (21)

 

possiamo ricavare l’espressione della pressione acustica, sostituendo la (15) nella (21) appena citata :

 

                                                       (22)

 

Risulta anche di semplice manipolazione il calcolo dell’impedenza Z in funzione della distanza r dal centro della sfera stessa. Essa, per quanto visto nella (1) è equivalente al rapporto locale tra pressione e velocità. Allora, sostituendo  (20) e (22) appena ricavate nella (1), otteniamo :

 

                                                                          (23)

 

in cui si aveva :

 

                                                                                                      (24)

 

In forma alternativa l’espressione di Z in funzione della distanza r può essere ulteriormente riscritta come :

 

                                                                            (25)

 

Dalle precedenti considerazioni scaturisce il grafico di seguito illustrato, che mostra l’andamento qualitativo della pressione acustica e della velocità delle particelle sempre in funzione della distanza dal centro della sfera sorgente :

                     P,u      P

                                            u

 

 

 


                                                                                 r

Fig.8 - Grafico andamento Pressione e Velocità in funzione di r

A parte l’andamento non rettilineo che ci si poteva immaginare, notiamo un fenomeno d’inversione delle due grandezze in prossimità dell’origine del riferimento (il centro della sfera). Man mano che ci si avvicina, la velocità tende a crescere molto più rapidamente di quanto non faccia la pressione, cosa che non succede lontano dall’origine, dove quest’ultima, pur andando a valori infinitesimi come la velocità, si mantiene sempre ad una soglia più sensibile. Ne scaturisce una riflessione del tutto generale : lontani dalla sorgente sonora, è più probabile udire un suono (l’orecchio umano è sensibile alla pressione acustica e la utilizza come “veicolo” sonoro) che avvertirne gli effetti perturbativi su particelle circostanti.

Anche il grafico seguente è utile per la comprensione di questi fenomeni :

 

        1,0                                                     

                    0,5

 

                   0,01                                        

 

               0,0001                                                       Kr

 

Fig.9- Grafico-esempio mostrato a lezione come lucido.

 

Come noto, consideriamo queste due uguaglianze :

 

                                                                                         (26)

 

da cui :

 

                                                                                                 (27)

 

In genere, un mezzo riproduttore del suono, quale un altoparlante, può assumere valori di Kr dell’ordine di 0,05

 

Effetto di prossimità

 

E’ degno di nota un fenomeno chiamato “di prossimità”, che si verifica con tutti i microfoni. Oggigiorno, per ricavare l’informazione trasportata dal suono, esistono dei trasduttori col compito di rilevare le variazioni di pressione e velocità acustiche chiamati microfoni. Sono oggetti che tutti bene o male conosciamo, ma molti potrebbero ignorare il fatto che, principalmente, ne esistono di due tipi : quelli sensibili alla pressione e quelli che, invece, rilevano la variazione di velocità. Ambedue, però, presentano il fenomeno prima citato, che può essere ritenuto pregio o difetto a seconda dei casi e dell’utilizzo a cui si deve destinare l’oggetto. Noi la consideriamo una caratteristica e come tale andiamo a definirla : per i microfoni “a pressione” l’avvicinamento alla sorgente del suono (pensiamo ad un cantante che muove lo stesso vicino e lontano dalla sua bocca) provoca un aumento dell’ampiezza del segnale riprodotto, anche se esso resta inalterato. L’effetto che percepiamo da questa operazione è un aumento considerevole di volume, anche se le altre caratteristiche restano invariate. Per quanto riguarda invece i microfoni “ a velocità”, essi presentano la stessa sensibilità alla distanza dalla sorgente sonora, ma questa ha influenza invece che sull’ampiezza del segnale riprodotto, sulla sua composizione in frequenza. Avvicinando lo stesso alla fonte del suono, pur fornendogli sempre lo stesso suono, vengono risaltate le componenti a bassa frequenza. Ne consegue un’uscita più cupa e marcata. Come anticipato prima, questa caratteristica, in maniera conscia o meno, viene sfruttata spesso dai cantanti che avvicinando un microfono a pressione possono simulare un aumento di volume pur senza innalzare troppo il loro grido, mentre, col modello di microfono a velocità, possono ottenere dei suoni bassi soddisfacentemente corposi, pur senza essere provetti baritoni, mentre possono risaltare al meglio i loro acuti semplicemente allontanando il microfono dalla bocca, evitando così di coprirli. Tale fenomeno spesso è indesiderato (pensiamo ai lirici che, abituati a cantare senza amplificazione di alcun genere, si trovano a netto disagio dovendo imparare a maneggiare dinamicamente il microfono). Pertanto mediante filtri elettronici è possibile appiattire ambedue i fenomeni citati, così da rendere la risposta del microfono pressoché costante in ogni situazione.

Il grafico di seguito illustrato è significativo dello sfasamento tra pressione e velocità nei pressi della sorgente. Analizziamolo :

 

      

 

 

 

 

 


         0                                      Kr

 

Fig.10 - Grafico dell’andamento della fase tra Pressione e Velocità in funzione del prodotto Kr

 

Quanto visibile è da spiegarsi in maniera molto semplice : avvicinandosi alla sorgente sferica, mentre la velocità u varia come 1/r, la pressione P varia invece come . Ne consegue un irrimediabile sfasamento.

 

Analisi intensimetrica dell’onda sferica

 

Partiamo dalle due grandezze ricavate, ora note : la pressione, come esposta nella (20) e la velocità, mostrata nella (22).

Riassumendo quest’ultima sappiamo che :

 

                                                                                   (28)

 

così come ricaviamo dalla (20) che :

 

                                                   (29)

 

Nota l’espressione dell’intensità :

 

                                                                                     (30)

 

possiamo scrivere la (30) come prodotto della (28) e (29) :

 

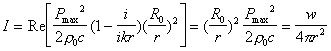                               (31)

 

che rappresenta la relazione di propagazione in campo libero, evento che è molto difficile da verificarsi a causa della costante presenza di corpi circostanti, di ogni genere, che modificano il moto ondulatorio prodotto dalla sfera.

 

 

Fine.