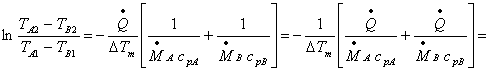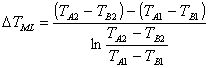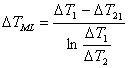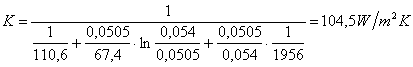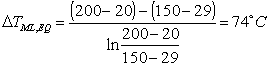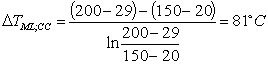Scambiatori di calore
Gli scambiatori di calore
sono macchine che permettono uno scambio termico, e quindi di entalpia, tra due
fluidi. In genere i fluidi sono separati da un divisorio metallico che
impedisce il contatto chimico, caratteristica indispensabile nei processi in
cui si vuole mantenere separato un fluido “pulito” (latte o altri liquidi
alimentari) da uno contaminato (acqua, olio,…). Non essendoci contatto le
pressioni dei fluidi possono anche essere molto diverse.
L’ esempio più importante
di utilizzo di uno scambiatore in cui i fluidi si miscelano è quello della
pastorizzazione del latte: in questo caso vapore ad alta temperatura si mischia
al latte per sterilizzarlo, separandosi poi a fine processo.
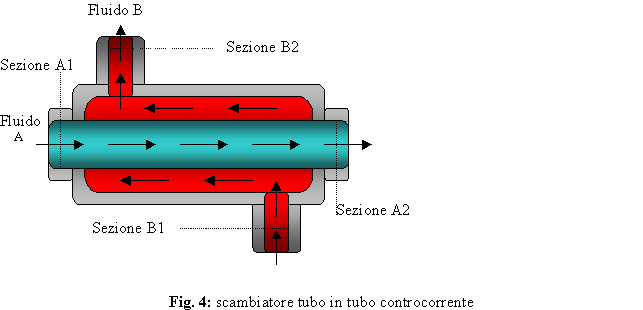
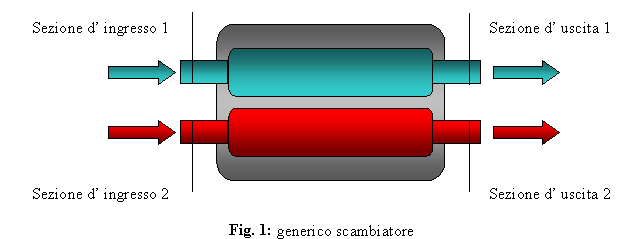
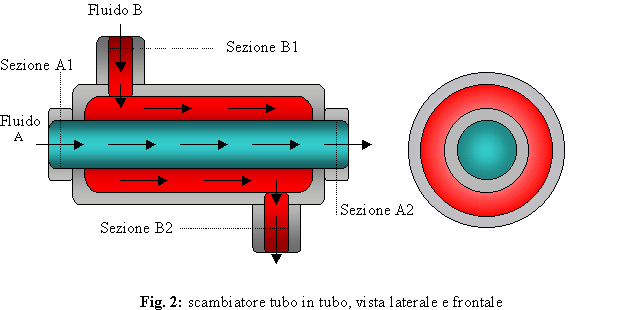
Il generico scambiatore è
un apparecchio avente due sezioni d’ ingresso e due d’ uscita:
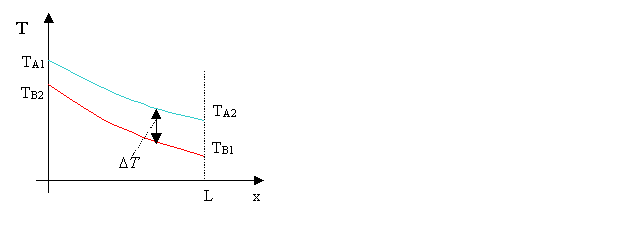
Bilancio entalpico, andamento della temperatura
Si nota facilmente che
gli scambiatori controcorrente sono particolarmente efficienti, mantenendo un DT elevato lungo tutto il tragitto. Addirittura può
accadere, come nel caso preso in esame nel grafico, che ![]() .
.
Esercizio
Il seguente esercizio mostra la valutazione delle prestazioni termodinamiche di uno scambiatore.
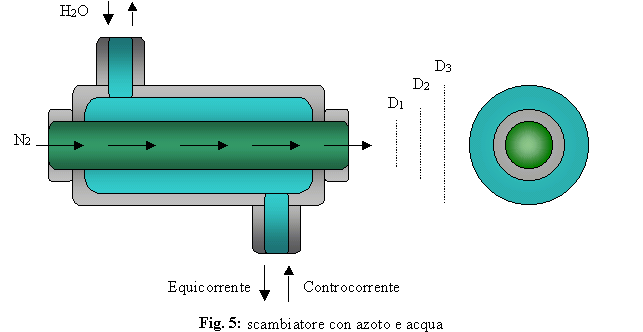
Sia dato uno scambiatore
avente come fluido di processo azoto, come fluido di servizio acqua.
Determinare la temperatura di uscita dell’ acqua e la superficie interna del
tubo nei casi lo scambiatore sia equicorrente e controcorrente.
Vengono forniti i
seguenti dati:
![]()
![]()
![]()
![]()
![]()
![]()
a)determino la
temperatura d’ uscita dell’ acqua, essa non dipende dal verso in cui scorre:
![]() (23)
(23)
i calori specifici sono
tabellati:![]() ,
, ![]()
ricavo così ![]() (verrà utile in
seguito) e
(verrà utile in
seguito) e ![]() :
:
![]() (24)
(24)
![]() (25)
(25)
![]()
L’ acqua ha un incremento
di temperatura modesto, del resto immetto molta più acqua che azoto, ed essa ha
un calore specifico quadruplo di quello dell’ azoto.
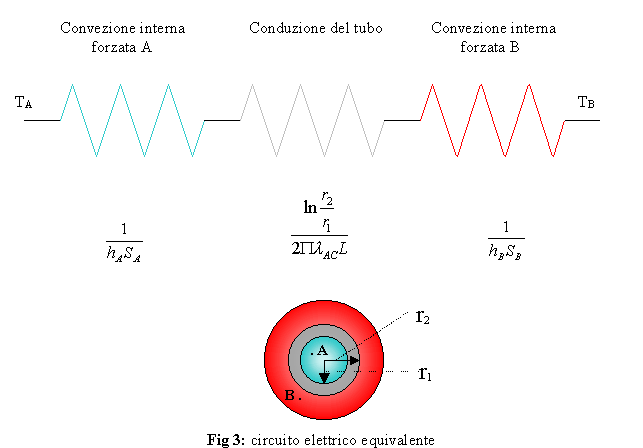
b)determino la superficie
interna del tubo; prima di procedere definisco il coefficiente globale di
scambio K come :
![]() (26)
(26)
Quindi:
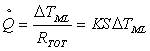 (27)
(27)
con: ![]()
Le lunghezze dei raggi di
tubo e camicia devono essere misure commerciali, reperibili cioè sul mercato.
Pongo:
![]() ,
, ![]() ,
, ![]()
K risulta essere:
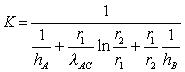 (28)
(28)
Dalle tabelle ricavo ![]() , ma
, ma ![]() e
e ![]() restano incognite.
restano incognite.
Parto cercando ![]() : si tratta di convezione forzata, è dunque ragionevole
applicare l’ equazione di Dittus-Boelter:
: si tratta di convezione forzata, è dunque ragionevole
applicare l’ equazione di Dittus-Boelter:
![]() (29)
(29)
Il numero di Prandtl è
tabellato: Pr = 0,71, ricavo il numero di Reynolds:
![]() (30)
(30)
La viscosità è tabellata:
![]() , manca la velocità, però so che:
, manca la velocità, però so che:
![]() (31)
(31)
con ![]() area interna:
area interna: ![]()
Essendo l’ azoto un gas
perfetto vale :
pv = RT
da cui ricavo la densità:
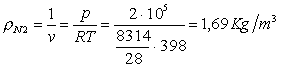 (32)
(32)
essendo ![]() ,
, ![]() la massa molare
dell’ azoto e T = 398K un ragionevole valor medio di temperatura tra ingresso e
uscita. Allora:
la massa molare
dell’ azoto e T = 398K un ragionevole valor medio di temperatura tra ingresso e
uscita. Allora:
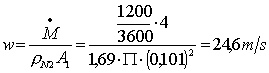 (33)
(33)
![]() (34)
(34)
Poiché l’ equazione di
Dittus-Boelter vale per ![]() , la posso usare, ottenendo così Nu:
, la posso usare, ottenendo così Nu:
![]() (35)
(35)
dalle tabelle ricavo: ![]() , posso così trovare
, posso così trovare ![]() :
:
![]() (36)
(36)
![]() (37)
(37)
Per trovare ![]() procedo nello stesso
modo, partendo dal numero di Reynolds:
procedo nello stesso
modo, partendo dal numero di Reynolds:
![]() (38)
(38)
L’ acqua scorre tra due
cilindri, devo dunque considerare il diametro idraulico equivalente:
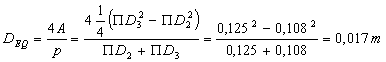 (39)
(39)
essendo p il perimetro
bagnato dall’ acqua. La viscosità dell’ acqua è tabellata: ![]() ; manca la velocità, che ricavo come già fatto per l’ azoto:
; manca la velocità, che ricavo come già fatto per l’ azoto:
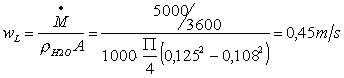 (40)
(40)
![]() (41)
(41)
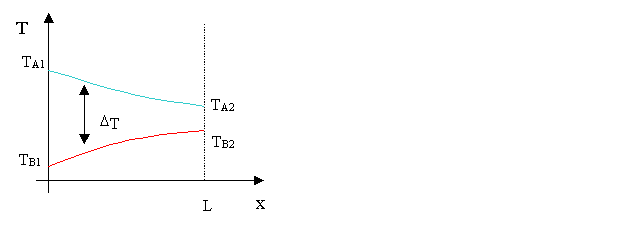
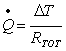
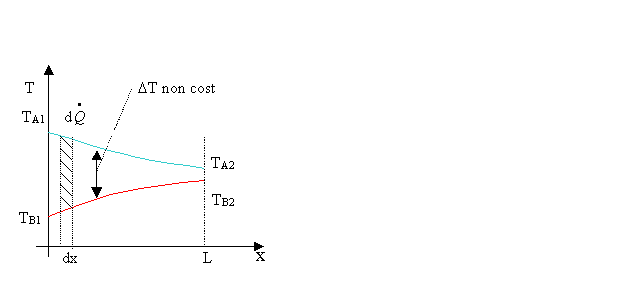
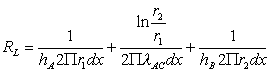
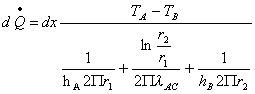

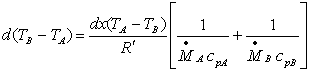
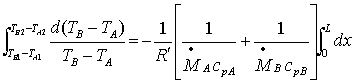
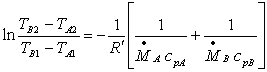
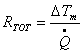 , sostituisco,
, sostituisco,