EQUAZIONI DEL MOTO ISOTERMO DEI FLUIDI
INTRODUZIONE
Le equazioni necessarie per descrivere il moto isotermo di un fluido sono due: una scalare ,data dall'equazione di continuità ,ed una vettoriale (quindi proiettabile lungo i tre assi di riferimento cartesiano) data dall'equazione di Navier.
Scopo di questo insieme di equazioni è determinare le incognite fluidodinamiche all'interno di una regione di flusso definita da una "pelle", che rappresenta il nostro sistema.
Le variabili u e p dipendono anche dal tempo, perché non sempre ci si trova in regime stazionario. Avremo quindi
![]()
![]()
L'EQUAZIONE DI CONTINUITA`
Il principio di conservazione della massa, valido per qualunque massa fluida in movimento, comporta un legame fra i caratteri cinematici del processo di moto e la densità del fluido; a questo legame viene dato il nome di equazione di continuità.
Isoliamo nel campo di moto un volume finito v racchiuso dalla "pelle" S, fissa rispetto alla terna di riferimento; siano u e r rispettivamente la velocità e la densità del fluido in corrispondenza dell' elemento infinitesimo di superficie dS al quale compete una normale n.
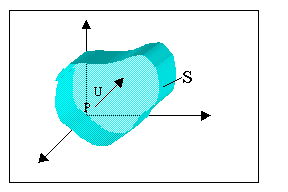
La variazione di massa nel nostro volume infinitesimo nell'unità di tempo è data dalla differenza tra la massa entrante e quella uscente:
![]()
Nell’intervallo di tempo dt attraverso la superficie del volume passa la massa
![]()
dove il segno negativo è dovuto al fatto che il vettore normale n e la direzione della massa entrante sono opposti. Questa differenza tra massa entrante ed uscente attraverso la superficie di contorno deve essere compensata dalla variazione che la massa
![]()
ha subito nello stesso intervallo dt per effetto dei cambiamenti di densità; deve perciò
essere:
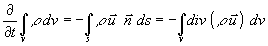
dove l'ultimo passaggio è dovuto al teorema di Gauss.
Data l'arbitrarietà del volume scelto, affinché i due integrali siano uguali, gli argomenti degli stessi devono essere uguali. Si ottiene quindi
![]()
che è l'equazione di continuità cercata. Solitamente noi ci occupiamo di fluidi in regime stazionario, dove tutti i punti sono nelle stesse condizioni perciò
![]()
Abbiamo quindi
![]()
Per le proprietà della divergenza
![]()
che significa che il campo delle velocità è solenoidale e, in termini fisici, che la portata entrante è uguale a quella uscente.
E' possibile dimostrare l'equazione di continuità anche in un altro modo, non usando integrali ma variazioni infinitesime su un volume dalla forma ben definita: un parallelepipedo di lati dx, dy, dz.
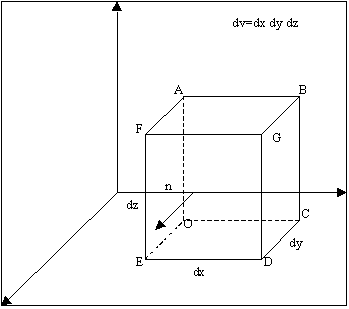
Siano ux, uy, uz le componenti della velocità e r la densità del fluido. Attraverso la faccia AOEF, di area dy dz, entra, nell’intervallo di tempo infinitesimo dt, la massa
![]()
Dalla faccia parallela BCDG, viceversa, esce la massa
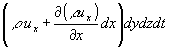
![]()
Analogamente,dalle altre coppie di facce del parallelepipedo escono le masse
![]()
![]()
Per il principio di conservazione della massa, la massa uscente nel tempo dt attraverso l'intera superficie di contorno del volume considerato
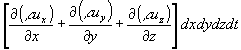
deve uguagliare la diminuzione
![]()
subita, nello stesso intervallo di tempo, per effetto della variazione della densità, dalla massa in esso ontenuta. L’equazione diventa quindi
![]()
che è l'equazione cercata.
Consideriamo ora un tubo di flusso
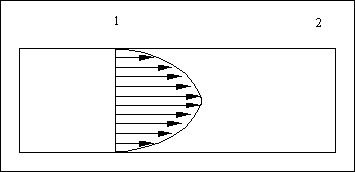
Consideriamo due sezioni, indipendentemente dal profilo assunto dal fluido nel tubo di flusso. Noteremo che in base all'equazione di continuità sono uguali non solo la portata in massa, ma anche la velocità del fluido stesso.
![]()
Ma
![]()
![]()
e quindi, supponendo la densità costante,
![]()
Consideriamo ora un altro caso
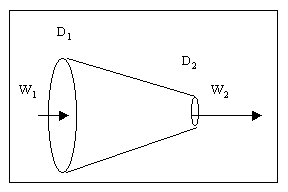
Supponiamo che valga la seguente relazione tra D1 e D2
![]()
Vogliamo calcolare la velocità di uscita del fluido dalla sezione 2, in funzione di quella nella sezione 1.Per fare questo uguagliamo le portate in massa, considerando costante la densità del fluido.
![]()
![]()
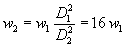
Quindi la velocità d'uscita è sedici volte quella d’entrata. In base a questa osservazione si spiegano tanti fenomeni dell'esperienza comune, per esempio perché quando si innaffia il giardino con una canna, se si vuole aumentare la gittata si cerca di diminuire la sezione del tubo con il dito: l'aumento di gittata è dovuto all'aumentata energia cinetica dell'acqua, non da un aumento di pressione. Infatti se volessimo chiederci la pressione d'uscita non avremmo bisogno di effettuare alcun calcolo: è sempre quella atmosferica.
EQUAZIONE DI NAVIER
Per introdurre l’equazione di Navier dobbiamo considerare un nuovo sistema di riferimento e dotarci di alcuni strumenti matematici che ci saranno utili nella spiegazione successiva.
Esistono due sistemi di riferimento:
In questa esposizione useremo un riferimento Lagrangiano.
Cerchiamo di evidenziare le principali differenze tra le due convenzioni. In un riferimento Euleriano l’accelerazione è data da
![]()
Quando ci mettiamo in un sistema Lagrangiano non possiamo più applicare semplicemente le derivate temporali , perché il sistema , nel tempo dt , trasla nello spazio insieme al fluido . Precisamente:
![]()
dove ds è l’ascissa curvilinea della traiettoria descritta dalla particella e i, j, k sono i versori degli assi cartesiani. Ciò vuol dire che ho anche dei termini di trasporto, che comporta che la descrizione dell'accelerazione richieda non la solita derivata temporale ma un altro tipo di derivata , la derivata sostanziale , così definita :
![]()
In pratica quando si deve derivare rispetto al tempo , si deve derivare anche lo spostamento rispetto alle direzioni lungo le quali è avvenuto. L’accelerazione diventerà quindi
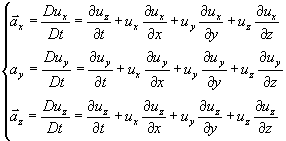
Voglio arrivare a scrivere una formula del tipo
![]()
dove la massa sarà
![]()
e l'accelerazione
![]()
Lo sforzo può considerarsi dato dalla sovrapposizione di due parti, una costituita dai soli sforzi normali dovuti alla pressione p, alla quale soltanto si fa riferimento quando si considera il fluido come perfetto, l'altra individuata dalle sei componenti che nascono durante il movimento a causa della viscosità, alle quali si deve attribuire il differente comportamento del fluido reale rispetto a quello perfetto. Si viene cosi a scomporre il tensore degli sforzi nella somma di una parte che possiamo chiamare idrostatica e di una parte che trae origine dal movimento.
In un fluido in movimento ci sono, quindi, due tipi di forze:
L'unica forza di massa presente è quella dovuta all'attrazione gravitazionale. Il potenziale gravitazionale è
![]()
e quindi la forza per unità di massa è
![]()
Le forze di volume si dividono a loro volta in
Analizziamo ora le forze normali
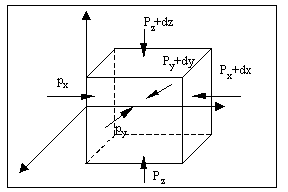
![]()
![]()
Analogamente per le componenti y e z
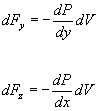
Da cui si ottiene che
![]()
Analizziamo le forze tangenziali
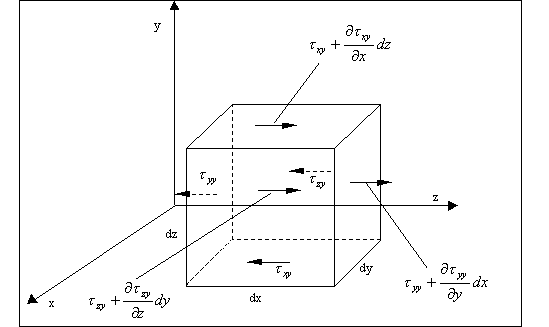
Scriviamo la risultante degli sforzi nella direzione y, cioè moltiplichiamo la differenza tra gli sforzi delle facce parallele per l'area della faccia stessa:
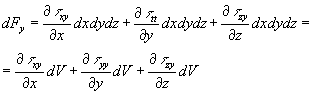
Ricordando ora la definizione di sforzo tangenziale si ha :
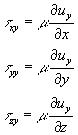
Quindi si ottiene, sostituendo in (38)
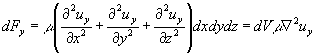
Tenendo conto infine delle componenti lungo x e z (che si calcolano in modo analogo) si ottiene lo sforzo complessivo:
![]()
L’equazione di Navier si può interpretare come la somma delle forze di massa, delle forze di pressione e di quelle tangenziali. Sostituendo le forze calcolate in (32),(37),(40) otteniamo
![]()
dove la differenza di segno sta ad indicare che i primi due termini accelerano il fluido mentre le forze tangenziali lo frenano. Ricordando ora l’espressione della forza con le derivate sostanziali ,e dividendo entrambi i membri per r dV otteniamo
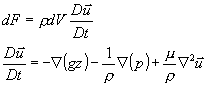
L’equazione (43) rappresenta l’equazione di Navier per un fluido incompressibile, nel quale , nel tempo dt considerato, non vi è variazione di massa. Per rimuovere questa ipotesi ,e dare quindi un’equazione più generale, dobbiamo introdurre la viscosità dinamica
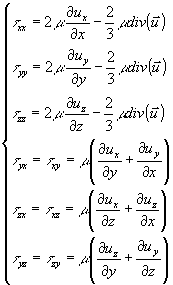
Questa definizione comporta una variazione del contributo dovuto alle forze viscose. Analizziamo ancora una volta per semplicità solo la componente y delle forze viscose : sostituiamo in (38) le nuove definizioni degli sforzi.
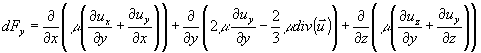
Svolgendo i conti
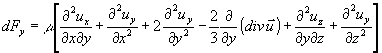
![]() Cioè
Cioè
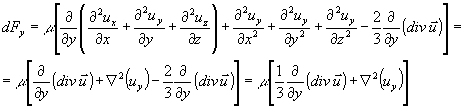
Analogamente per le altre componenti della forza quindi
![]()
Sommando infine tutti i componenti si ottiene la formula più generale
![]()
In condizioni stazionarie la divergenza del vettore u si annulla di modo che si ritorna all’equazione ( 43) e nel caso di fluidi perfetti si riconduce all’equazione di Eulero
![]()
L'equazione più generale è piuttosto complicata e viene integrata solo in pochissimi casi, ma è molto utile per impostare algoritmi numerici per la risoluzione del moto dei fluidi e per la teoria dei modelli.