ANALISI IN FREQUENZA
Lo scopo dell’analisi in frequenza è quello di definire il contenuto di un suono complesso, che contiene componenti a diverse frequenze, anche variabili istantaneamente.
Ricordando che il campo sonoro udibile umano va circa dai 20 Hz ai 20 kHz e che l’orecchio non percepisce tutte le frequenze allo stesso modo, si capisce come mai in molte applicazioni tecniche che vanno dalla registrazione e riproduzione della musica all’analisi del rumore prodotto da macchinari o ambienti, si è interessati a valutare non tanto il livello sonoro complessivo, cioè l’energia totale del suono, bensì la sua distribuzione alle varie frequenze.
In natura non esistono però solo suoni puri (le sinusoidi utilizzate in teoria e molto comode per un’analisi matematica sono molto lontane dalla realtà); sono presenti forme d’onda molto strane (ad esempio dall’analisi della voce umana si nota che essa non ha nulla a che fare con una semplice sinusoide). Anche il suono prodotto da uno strumento musicale (una ben precisa nota) non è fatto unicamente di sinusoidi.
In un suono reale sono quindi sempre presenti sinusoidi discrete con opportune ampiezze, frequenze e fasi alle quali è sovrapposta una quota di rumore.
Effettuare l’analisi in frequenza significa partire da una rappresentazione del suono nel dominio del tempo, cioè dalla forma d’onda, ed arrivare a definire lo spettro (un procedimento analogo è fatto nell’ottica dove la luce è scomposta nelle sue componenti cromatiche, nient’altro che onde a diversa frequenza).
Spettro
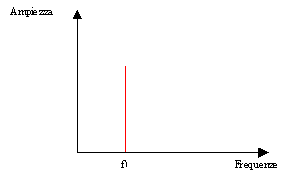
Si tratta di una rappresentazione grafica su un diagramma cartesiano che presenta in ascissa le frequenze ed in ordinata una grandezza rappresentativa dell’ampiezza del suono (fig. 1).
Nel caso più semplice dell’utilizzo di un microfono (che non è altro che un trasduttore di pressione), il segnale ottenuto potrà essere mappato come livello di pressione dopo essere stato messo in scala logaritmica (dB).

Fig. 1 – Spettro di un tono puro
Un tono puro (in altre parole una sinusoide) è facilmente rappresentato come una singola riga spettrale: lo spettro vale quindi zero a tutte le frequenze, salvo una particolare frequenza (nell’esempio sopra f1) dove si otterrà un particolare valore, che corrisponde alla pressione RMS del trasduttore. In corrispondenza di f1 vi è dunque la cosiddetta componente armonica fondamentale.
Ciò nonostante, questo è un caso puramente teorico: in generale, infatti, lo spettro di un segnale non è costituito da una singola riga ad una ben precisa frequenza.
Se un segnale complesso ha, oltre che alla fondamentale f1, anche altre armoniche a frequenze multipli interi di f1, il suono è definito armonico e le righe spettrali sono dette: 1a armonica, 2a armonica, ecc.
Un suono complesso è, in ogni caso, periodico con un periodo T corrispondente alla frequenza fondamentale.
Ad esempio con f1 = 1000 Hz, il periodo sarà: T = 1/f = 1ms.
Anche un segnale periodico costituisce un caso particolare: in natura, infatti, si possono trovare parecchi suoni armonici complessi aperiodici. In questi ultimi, pur restando costanti nel tempo le ampiezze delle componenti armoniche, cambiano le fasi e di conseguenza la forma d’onda si deforma.
Esiste anche un suono definito disarmonico nel quale vi sono componenti a frequenze che non sono multipli esatti della fondamentale (vi possono essere anche delle sub-armoniche). Anche questa è, comunque, una rappresentazione spettrale per righe isolate.
Uno stesso segnale si può in ogni caso rappresentare con spettri di diverso tipo.
Le conversioni dal dominio del tempo a quello della frequenza sono, infatti, sempre imprecise: non esiste, a tutt’oggi, un’apparecchiatura in grado di riprodurre fedelmente i fenomeni di analisi in frequenza che avvengono nel nostro orecchio, che rimane quindi un apparato migliore di qualunque macchinario realizzato.
Per un segnale stazionario, cioè costante nel tempo, l’analisi è facilmente realizzabile esaminando una frequenza alla volta.
Rumore
Il rumore (noise) è un segnale in banda larga, d’andamento casuale nel tempo, assolutamente aperiodico, che si sovrappone al segnale utile e che pertanto ne influenza l’intelligibilità; a causa del rumore si ha quindi un limite sotto al quale il segnale utile non è più rilevabile in modo soddisfacente.
Su un qualunque intervallo di frequenze che si estende da f1 a f2, l’energia del rumore è continua cioè infinitamente densa su tutto lo spettro (non è possibile trovare zone prive d’energia così come invece era nel caso di un suono disarmonico complesso).
Per l’energia contenuta in un campo di frequenze, vale la relazione:
![]()
Filtri d’ottava e a frazione d’ottava
Un primo metodo per effettuare l’analisi in frequenza dei segnali stazionari prevede l’utilizzo di un "banco" di filtri passa – banda (come i filtri d’ottava), vale a dire di una serie di dispositivi ciascuno dei quali permette il passaggio solo di un determinato range di frequenze, escludendo le componenti del suono a frequenze maggiori e minori. Con uno strumento di misura all’uscita d’ogni filtro, è possibile misurare il livello che compete al particolare intervallo di frequenze (fig. 2).
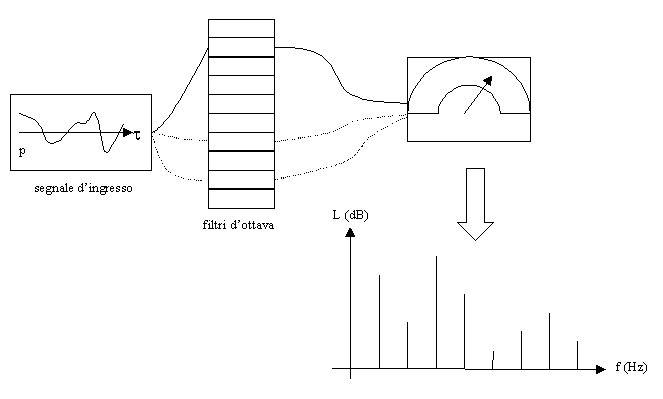
Fig. 2 – Banco di filtri passa-banda
Graficamente è possibile rappresentare un filtro passa-banda con una zona in cui il guadagno è pressoché costante e pari a 0 Db (banda efficace, D f) e con due zone, esterne alla prima, in cui il guadagno è trascurabile (fig. 3). La banda efficace è compresa tra f1 e f2, dette frequenze di taglio, poste a metà energia rispetto alla banda passante; per definizione G(f1) = G(f2) = -3 db. fc è definita frequenza di centro banda ed è tale che G(fc) = 0 db.
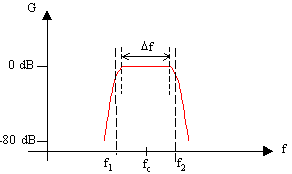
Fig. 3 – Guadagno di un filtro passa-banda
Teoricamente, un filtro ideale dovrebbe avere come curva del guadagno un impulso rettangolare, ma essendo il dispositivo realizzato con componenti passivi i fronti di salita e di discesa non potranno mai essere perfettamente verticali.
La pendenza dei fronti della caratteristica deve comunque essere contenuta all’interno di una tolleranza definita dall’I.E.C., (organizzazione che si occupa della definizione degli standard per le misure acustiche).
Fondamentalmente esistono due spettri per bande: lo spettro a bande costanti, in cui tutte le bande hanno la stessa ampiezza, e lo spettro a bande percentuali costanti, in cui ogni banda è ampia il doppio della precedente.
Si definisce quindi l’ottava come intervallo in cui la frequenza minima (f1) e quella massima (f2) verificano le relazioni:
![]()
In sostanza, la frequenza massima è esattamente il doppio della minima.
In molte applicazioni, però, la suddivisione dell’asse delle frequenze in bande d’ottava è approssimativa: vi è quindi la necessità di usare filtri a banda più stretta (a frazione d’ottava), che mantengano però sempre la proporzione tra la larghezza di banda e la frequenza di centro banda:
![]()
Per i filtri d'ottava, questa costante è pari a:
![]()
In questo modo la frequenza massima di un filtro è sempre uguale alla minima del successivo. Questi sono appunto i filtri ad apertura percentuale costante.
Esistono quindi diversi tipi di filtri, in base al numero di parti in cui è divisa ogni banda:
Tra queste, la più nota è quella in 1/3 d’ottava: il suo utilizzo è dovuto principalmente al fatto che corrisponde con buon’approssimazione al sistema uditivo umano soprattutto per frequenze al di sopra dei 600 Hz (al di sotto di questo valore non è infatti possibile ricostruire la crescente risoluzione del nostro udito).
Ad esempio possiamo calcolare quanti filtri occorrono per coprire l’intero campo delle frequenze udibili. Per far questo prendiamo dei filtri ciascuno dei quali ha una frequenza di centro banda doppia di quella del filtro precedente. (il tutto è disciplinato da norme I.S.O.):
|
fc1 |
fc2 |
fc3 |
fc4 |
fc5 |
fc6 |
fc7 |
fc8 |
fc9 |
fc10 |
|
31,5 Hz |
63 Hz |
125 Hz |
250 Hz |
500 Hz |
1 kHz |
2 kHz |
4 kHz |
8 kHz |
16 kHz |
Tab. 1
Dalla tabella precedente si nota che con 10 filtri d’ottava viene coperto l’intero spettro udibile in quanto il filtro centrato a 16 kHz arriva a coprire oltre i 20 kHz e quello a 31,5 Hz arriva a frequenze inferiori di 20 Hz.
Dal momento in cui in ogni ottava vi sono tre terzi d’ottava, il numero di filtri in terzi d’ottava cresce a 30.
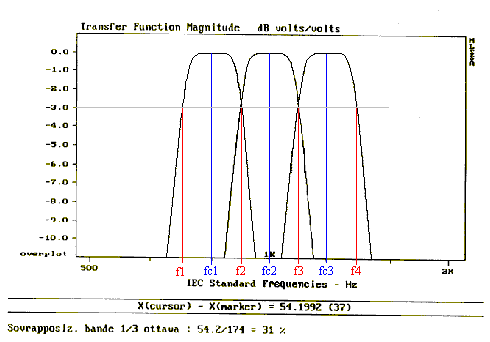
Fig. 4
Dalla fig. 4 è possibile vedere che i filtri non separano mai perfettamente le frequenze. Vi è infatti un’elevata probabilità che un suono puro cada nella zona in cui due bande da 1/3 d’ottava si sovrappongono. Ad esempio, in presenza di una componente alla frequenza f3, lo spettro rileverà un’energia sia nella banda inferiore che in quella superiore. Questo fenomeno si presenta spesso dato che la sovrapposizione è circa del 31% (ciò sarà successivamente dimostrato).
Analisi software dello spettro
Vediamo ora come e’ possibile analizzare un segnale audio attraverso un personal computer, con l’ausilio di un particolare software: SpectraRTA (RTA sta per Real Time Analyzer: analizzatore in tempo reale).
Il programma è direttamente scaricabile dal sito www.soundtechnology.com.
Altri software utili per l’analisi di un segnale sono:
Questo programma permette un’analisi in frequenza, sia di un segnale inserito via microfono, sia di uno generato internamente dal programma stesso. Permette inoltre di analizzare il suono in differenti modi: con bande d’ottava, in terzi, in sesti, in noni o dodicesimi d’ottava (aumentando la risoluzione), ponderando il segnale con le curve A, B, C. Inoltre, è possibile impostare il range di frequenze da analizzare ed osservare il valore istantaneo del segnale che può essere calcolato con tempo d’integrazione FAST (125 ms), SLOW (1 s), IMPULSE oppure con un periodo infinito (FOREVER). Infine, è consentito effettuare misure della durata di pochi secondi, alcuni minuti, ma anche di qualche ora o giorno (nel campo del rumore ambientale, ad esempio, la norma italiana prevede misure di un’ora, calcolando poi il valore complessivo riferito alle 14 ore del periodo diurno (dalle 6 alle 22) e alle 8 ore di quello notturno(dalle 22 alle 6)). Tutto ciò è definibile attraverso la funzione options à settings.
Ci occupiamo ora unicamente di SpectraRTA come analizzatore di spettro in terzi d’ottava.
In primo luogo è necessario calibrare il software. Generando un tono puro da 1KHz (attraverso il generatore di segnali incluso in SpectraRTA) a 94dB, attraverso l’apposita funzione options à calibration si procede alla calibrazione, verificando poi che il tono sia esattamente valutato 94dB.
Si noti che l’asse delle frequenze è logaritmico (in SpectraRTA non è possibile avere l’asse lineare): questo perché normalmente le analisi in terzi d’ottava sono fatte con l’asse delle frequenze in scala logaritmica.
Bisogna specificare che i filtri di quest’analizzatore SW sono implementati con un algoritmo di calcolo numerico; pertanto presentano un’elevata capacità di separazione delle frequenze: sono filtri con fianchi molto ripidi. Ovviamente ciò non è ottenibile con analizzatori analogici, che presentano sempre bande sovrapposte.
Il primo segnale che andiamo ad analizzare è quello del rumore bianco (anch’esso generato via SW). Si ricorda che per rumore bianco (white noise) s’intende un rumore che ha uno spettro uniforme con densità spettrale costante a tutte le frequenze. Il suo nome è dovuto al fatto che comprende tutte le frequenze (da 20 Hz a 20 kHz), così come il bianco comprende tutta la banda di colori.
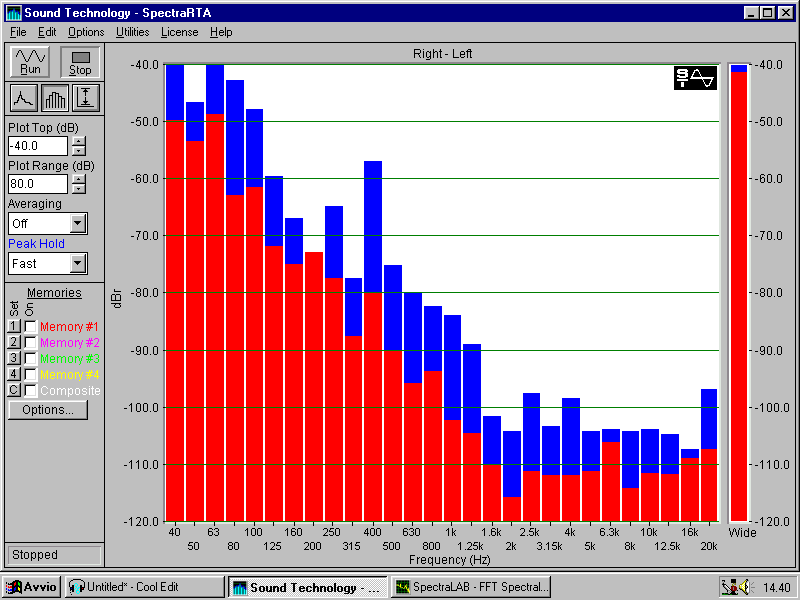
Fig. 5 – Rumore bianco visto in terzi d’ottava
Andiamo ora ad analizzare un rumore rosa, che presenta uno spettro piatto in un analizzatore in terzi d’ottava:
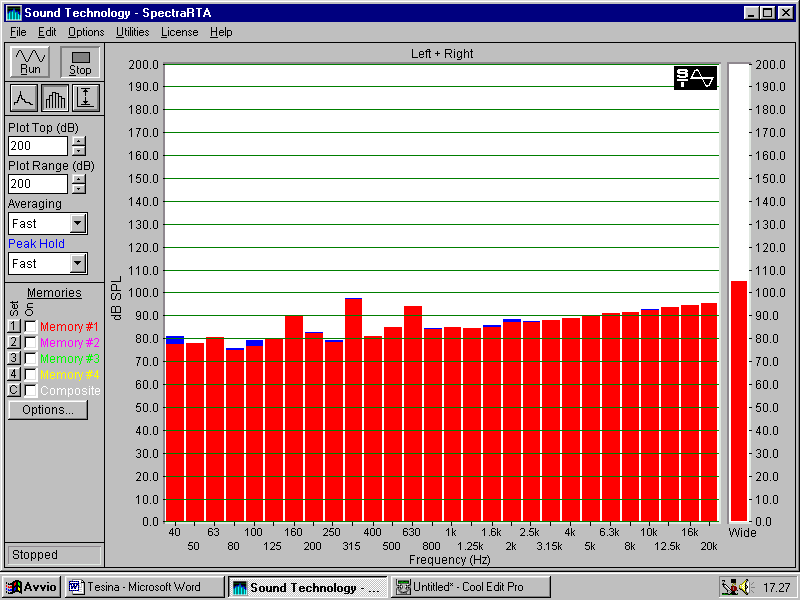
Fig. 6 – Rumore rosa visto in terzi d’ottava
Come ci aspettavamo, lo spettro è praticamente piatto. Il non perfetto appiattimento dipende dalla scarsa qualità della scheda audio del PC (strumento non professionale).
Una terza analisi presenta il confronto tra uno stesso segnale, prima lineare (fig.7) e poi ponderato A (fig. 8). Ricordiamo che la ponderazione A è un particolare tipo di equalizzazione che esalta le frequenze maggiormente percepite dall’uomo e taglia quelle meno udibili (ovvero quelle basse). Per questa prova s’inserisce tramite microfono il segnale sonoro prodotto dalla voce umana. Il segnale non ponderato si presenta nel seguente modo:
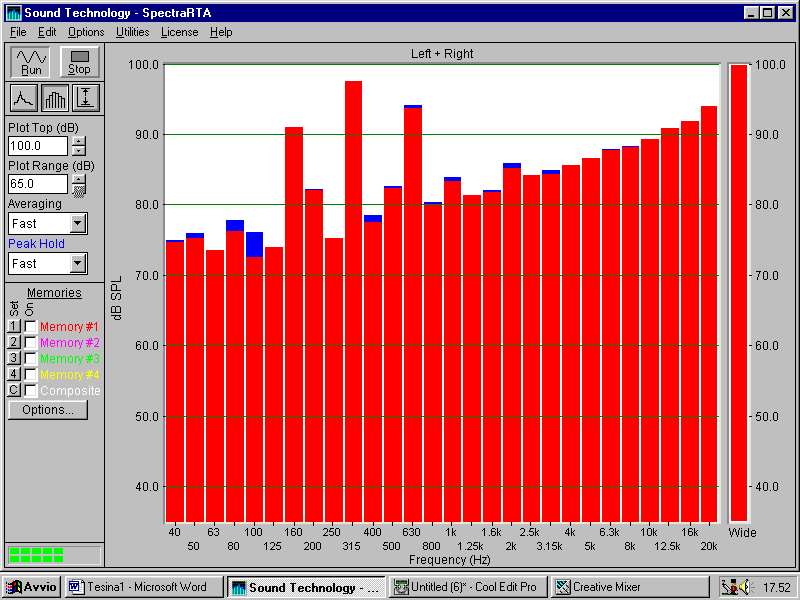
Fig. 7 – Segnale non ponderato
Applichiamo ora la ponderazione A (fig. 8): ciò che si nota è una forte attenuazione delle basse frequenze, presenti invece nel segnale non ponderato.
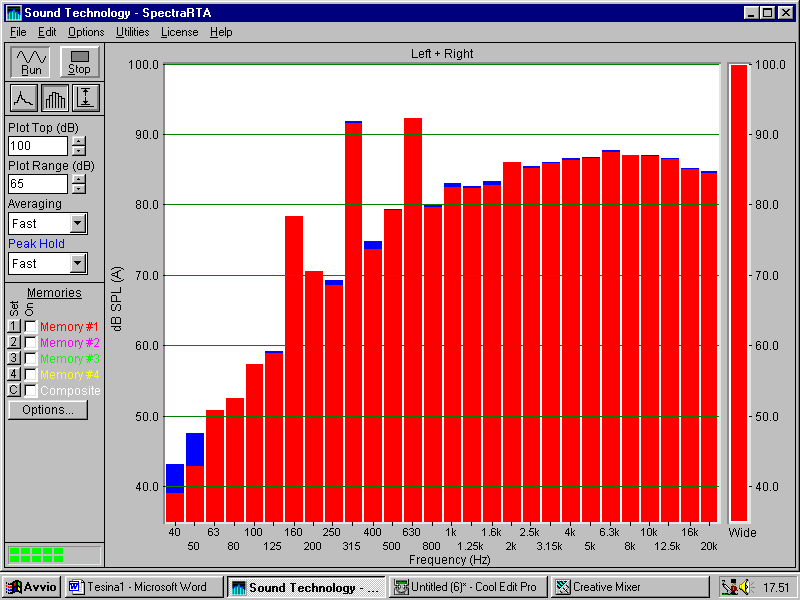
Fig. 8 – Segnale ponderato A
Specifichiamo che la sottile barra alla destra dello spettro rappresenta il segnale "totale" di quel canale, cioè presenta la somma di tutte le energie, mostrandone il valore non ponderato.
In questo caso, il segnale è ponderato via software, anziché per via analogica come farebbe uno strumento come il fonometro. Questo tipo di ponderazione, ampiamente criticata, si rivela comunque buona: il metodo via SW infatti, porta a risultati praticamente identici al metodo HW.
Per rappresentare al meglio ciò che il nostro sistema uditivo percepisce è bene lavorare in terzi d’ottava, con una costante d’integrazione FAST e inserendo la curva di ponderazione A.
Un difetto presente in SpectraRTA è l’impossibilità di visualizzare lo spettro minimo, che è invece richiesto dalla normativa italiana. La normativa del nostro paese, una delle più avanzate, è di difficile attuazione a causa della mancanza di strumenti in grado di effettuare le misure richieste.
Una soluzione a questo problema è l’utilizzo di un software come Excel nel qual è possibile copiare in forma numerica lo spettro valutato con SpectraRTA: in questo modo si possono visualizzare i dati tabulati ed elaborarli al fine di una particolare analisi.
Regolazione delle misure acustiche
In Italia, la regolazione delle misure acustiche è stata attuata tramite il decreto misure del marzo '98 (di seguito sono riportate solo le parti che a noi interessano maggiormente: l’intero teso è scaricabile dal sito www.assoacustici.it). Esso afferma che sul suono misurato possono essere effettuate tre possibili correzioni:
Per ogni correzione di questo tipo vengono addizionati 3 dB e il livello del rumore ambientale L è dato dalla somma:
L = Leq + C1 + C2 + C3
Ma come riconoscere le componenti tonali?
"Al fine di individuare la presenza di componenti tonali nel rumore, si effettua:
Il decreto richiede quindi di fare un’analisi spettrale per bande normalizzate in 1/3 d’ottava, considerando solo le componenti di carattere stazionario (in tempo e in frequenza). Si deve poi determinare il minimo d’ogni banda con costante di tempo FAST e realizzare il diagramma frequenza per frequenza delle bande così normalizzate.
Il decreto quindi continua:
"Si è in presenza di una componenti tonale se il livello minimo di una banda supera i livelli minimi delle bande adiacenti per almeno 5 dB"
Si può presentare un problema: i filtri in 1/3 d’ottava hanno i fianchi non perfettamente verticali (fig. 9), dunque si ha una parziale sovrapposizione di due bande Questo nasconde la possibile presenza della componente tonale, in quanto fa elevare allo stesso modo due bande vicine.
Siccome l’ampiezza del terzo d’ottava è di circa 174 Hz e che la zona d’incrocio tra due bande è approssimativamente di 54 Hz, vi è un’elevata probabilità (del 31%) che il tono puro cada in questo range. La presenza di un tono puro in questo intervallo non sarebbe quindi passibile di penalizzazione.
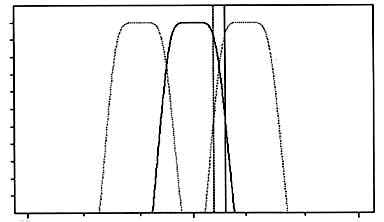
Fig. 9 -
Grafico del filtro di 1/3 d’ottava
Per ovviare a questo problema, il decreto afferma che:
"Per evidenziare componenti tonali che si trovano alla frequenza d’incrocio di due filtri ad 1/3 d’ottava, possono essere usati filtri con potere selettivo maggiore o con frequenze d’incrocio alternative."
Per effettuare questa misura, però, sarebbero necessari appositi filtri che, non essendo a norma IEC, non sono in vendita. Bisognerebbe inoltre effettuare per due volte la misura: questo non sempre è possibile poiché alcuni eventi si ripresentano solo dopo lunghi periodi.
Una soluzione potrebbe essere registrare il segnale senza perdere nessuna informazione e senza introdurre disturbi su disco fisso nel computer o su un sistema di registrazione "privo di perdite".
Attualmente la soluzione migliore prevede di effettuare una misurazione in 1/6 di ottava e poi riunire nei due differenti modi possibili (Fig. 10 a) e b)) i 1/6 per formare due grafici in 1/3 di ottava con frequenze di centro banda a norma e non: confrontando i due casi si potrà determinare la presenza o meno delle componenti tonali.
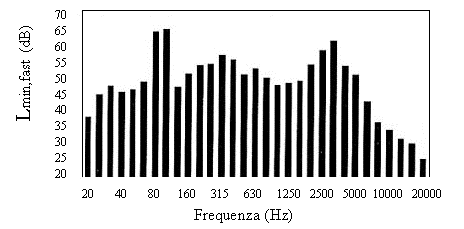
Fig. 10 a) -
Spettro in terzi d’ottava (primo modo)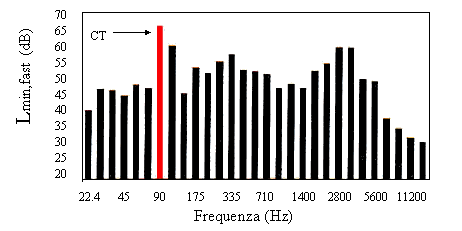
Fig. 10 b) -
Spettro in terzi d’ottava (secondo modo)
Ma, prima di applicare il fattore di correzione di 3 dB(A), la normativa prevede un ulteriore controllo:
"Si applica il fattore di correzione solamente se la componente tonale tocca un’isofonica eguale o superiore a quella più elevata raggiunta dalle altre componenti dello spettro."
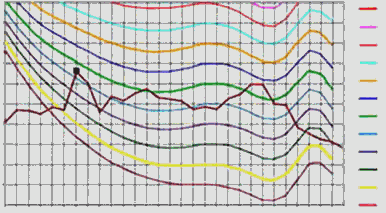
Fig. 11 -
Verifica della componente tonale con le isofoniche
Osservando lo spettro sembra che questo abbia una componente tonale a 80 Hz che svetta sulle altre, cioè che raggiunge l'altezza maggiore. Considerando, però, l'isofonica verde al centro del digramma di Fletcher e Manson, si nota che altre due vette, più elevate di quella a 80 Hz, la intersecano e la superano. Ciò significa che la componente tonale a 80 Hz non è penalizzabile con il fattore correttivo, in quanto non "svetta" sul diagramma delle isofoniche.
Il decreto prevede anche la possibile presenza di una componente tonale a bassa frequenza.
"Se l’analisi in frequenza svolta con le modalità precedentemente esposte, rivela la presenza di componenti tonali tali da consentire l’applicazione del fattore correttivo C2 nell’intervallo di frequenze compreso fra 20 Hz e 200 Hz, si applica anche la correzione C3, esclusivamente nel tempo di riferimento notturno."
Siamo in presenza di una componente tonale a bassa frequenza se sono verificate le tre seguenti condizioni:
In questo caso oltre alla normale correzione per componente tonale, è applicata anche quella per componente tonale a bassa frequenza (sempre di 3 dB(A) ).
I decreti che regolano le misure acustiche sono presenti solamente in pochi paesi: ciò accade perché il criterio con cui queste norme devono essere applicate è talmente restrittivo che nel 95-98% dei casi non sono necessarie eventuali correzioni.
Somma di segnali
Somma coerente
Dati due segnali sonori è possibile calcolare i livelli associati nei due casi:
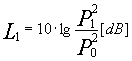
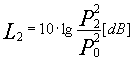
Se i due segnali sono perfettamente in fase, istante per istante le due pressioni sonore possono essere sommate per trovare un livello totale:
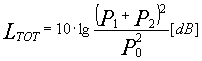
Se, inoltre, P1=P2:
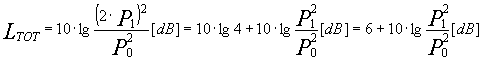
Sommando in pressione due livelli si ottiene un incremento massimo di 6 dB.
Per cui giungiamo all’inaspettato risultato che ![]() .
.
Somma incoerente
Nel caso in cui si abbiano a disposizione due altoparlanti che emettono lo stesso segnale, ricevere con un microfono due suoni assolutamente identici è praticamente impossibile: spesso, infatti, due segnali sono già lievemente differenti in partenza e percorrono distanze diverse prima di raggiungere il microfono. In un punto arbitrariamente lontano, quindi, a volte i segnali si sommano raddoppiando la pressione sonora, s'annullano oppure si presentano sono a fasi intermedie.
Generalmente, per somma di due livelli si considera una somma incoerente.
Quindi, per ottenere il livello sonoro totale si sfrutta il principio di conservazione dell'energia: esso prevede che la densità d'energia sonora sia uguale alla somma aritmetica delle due prese singolarmente.
Fig. 12: Somma incoerente
Quindi, sommando le intensità dei due segnali si ottiene:
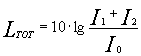
Se I1=I2 allora:
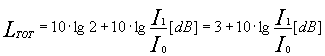
Per cui, ad esempio, ![]() e non
e non ![]() .
.
Possiamo quindi affermare che: sommando due livelli L1 ed L2, si ottiene un segnale che è dato dal maggiore dei due incrementato al massimo di 3 dB (lo si può notare anche dal grafico seguente).
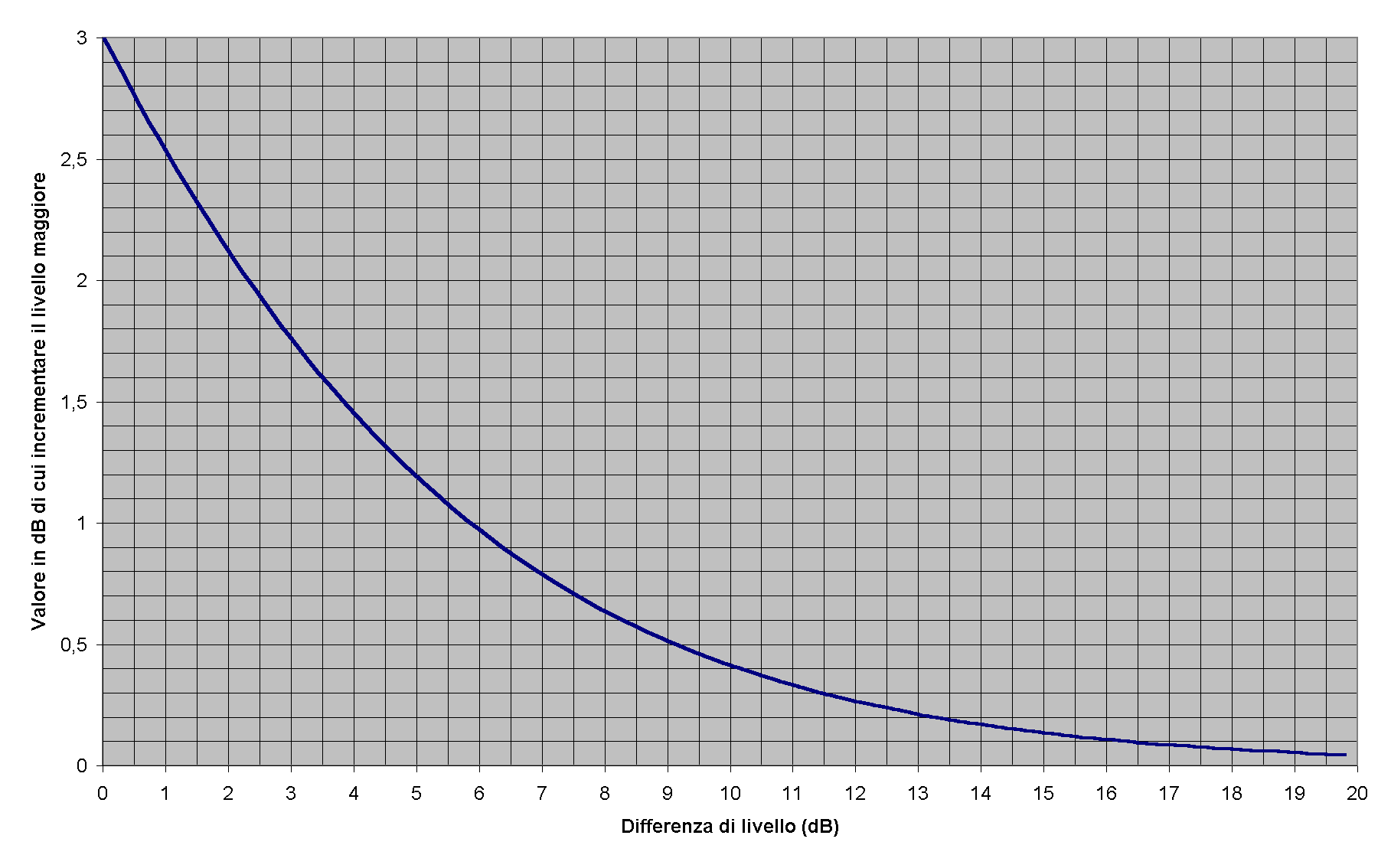
Fig. 13
Dalle proprietà del logaritmo possiamo inoltre capire che il valore da sommare al maggiore dei due suoni dipende unicamente dalla differenza di livello tra i due, non dal livello di partenza.
In fig. 13 è indicato quanto si deve sommare al livello del maggiore tra i due segnali per ottenere il livello totale.
Come si può notare, se i due livelli differiscono per più di 10 dB, l’incremento sul maggiore è sostanzialmente nullo (di soli +0,4 dB).
Ad esempio ![]() .
.
Supponiamo allora di essere in presenza di una sorgente forte e di una debole: l’orecchio umano percepisce entrambe le sorgenti, un fonometro invece soltanto la prima. Il suono è quindi trascurabile dal punto di vista del livello totale, ma è comunque udibile (sempre che non sia presente il fenomeno del mascheramento).
Interferenza
In presenza dello stesso segnale riprodotto da due altoparlanti si possono avere effetti di interferenza: vi sono, cioè, zone in cui i due segnali sono in fase (la somma avviene in pressione per un incremento massimo di 6 dB) ed altre in cui essi sono in controfase (uno ha un massimo e l’altro un minimo). In queste zone i due segnali elidono mutuamente i loro effetti. In particolare, i minimi d’intensità si trovano a distanza proporzionale a mezza lunghezza d’onda.
Gli effetti d’interferenza sono problematici quando si hanno solo due sorgenti di segnale. Con più sorgenti sarebbe praticamente impossibile trovare un punto in cui il segnale totale si annulla completamente.
L’operazione di cancellazione di un suono con un controsuono è praticamente irrealizzabile in una vasta regione: solo in condizioni geometriche molto favorevoli è ottenibile una zona di cancellazione più grande di ¼ di lunghezza d’onda. In condizioni normali, invece, le bolle silenti che si vengono a creare sono relativamente piccole (già ad una frequenza di 1000 Hz ho una lunghezza d’onda di 34 cm e quindi una bolla di raggio molto piccolo).
Esercizio: ponderazione di un suono
Per raggiungere una buona approssimazione della risposta umana occorre compensare strumentalmente il fatto che l'orecchio sente meglio le frequenze alte rispetto alle basse: questo avviene utilizzando le differenti curve di ponderazione.
Per il nostro scopo sarà utile avere a disposizione la sola curva A(fig. 14, tab. 2). Le altre possibili curve di ponderazione sono le curve B e D, non prese in considerazione dalla legge, e la curva C, utilizzata solo per rumori molto forti.
Si utilizza principalmente la curva A perché:
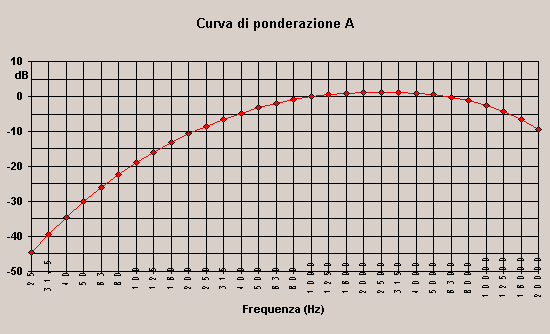
Fig. 14
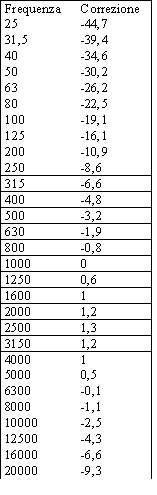
Tab. 2 - Ponderazione A
Dato, quindi, un segnale sonoro di cui si conosce lo spettro, si determini il livello totale lineare e ponderato. I dati necessari alla soluzione sono riportati nella tab.3:
|
Frequenza |
Livello in dB |
Livello in dB(A) |
|
125 |
88 |
71,9 |
|
250 |
84 |
75,4 |
|
500 |
80 |
76,8 |
|
1000 |
79 |
79 |
|
2000 |
76 |
77,2 |
|
4000 |
78 |
79 |
Tab. 3
Il livello in dB(A) è ottenuto sommando al valore in dB il rispettivo fattore di correzione (in tab. 2).
Il livello totale in dB è facilmente calcolabile e vale:
![]()
Ci proponiamo ora di calcolare il livello ponderato A: è sufficiente, ad ogni frequenza, applicare i fattori correttivi tabulati:
![]()
Come possiamo notare, il livello in dB(A) è significativamente più basso di quello in dB: questo perché l’utilizzo della curva di ponderazione A porta all’eliminazione di un’elevata quantità di rumore presente in bassa frequenza.
Importante è notare che la seconda cifra decimale del risultato ottenuto e, in generale, di qualsiasi livello sonoro espresso in dB o dB(A), non ha alcun significato fisico: infatti, la sensibilità dell'orecchio umano e di molti strumenti non arriva nemmeno al decimo di decibel.
La rappresentazione grafica seguente (in istogrammi) riporta i livelli del precedente segnale alle diverse frequenze. Da una prima analisi saremmo indotti a pensare che prevalga la componente a 125 Hz. In realtà, però, sono molto più udibili quelle ad alta frequenza (alle quali corrisponde un maggiore valore in dB(A)).
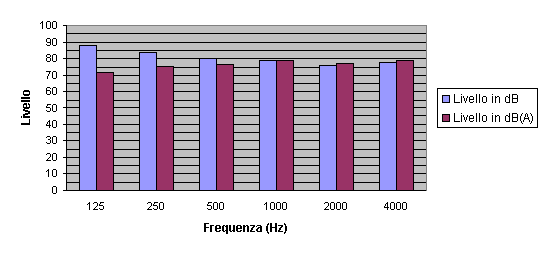
Fig. 15
Vari tipi di rappresentazione dello spettro
Uno spettro, a seconda della tecnica utilizzata per ricavarlo e del tipo di visualizzazione impiegata, può cambiare notevolmente d’aspetto. Esiste, infatti, una prima differenza tra l’analisi in banda stretta e in banda percentuale costante, ed una seconda differenza nella rappresentazione con asse delle frequenze lineare e logaritmica.
Prendiamo, di seguito, in esame lo spettro di uno stesso segnale, analizzato con lo stesso strumento e rappresentato in quattro differenti modi.
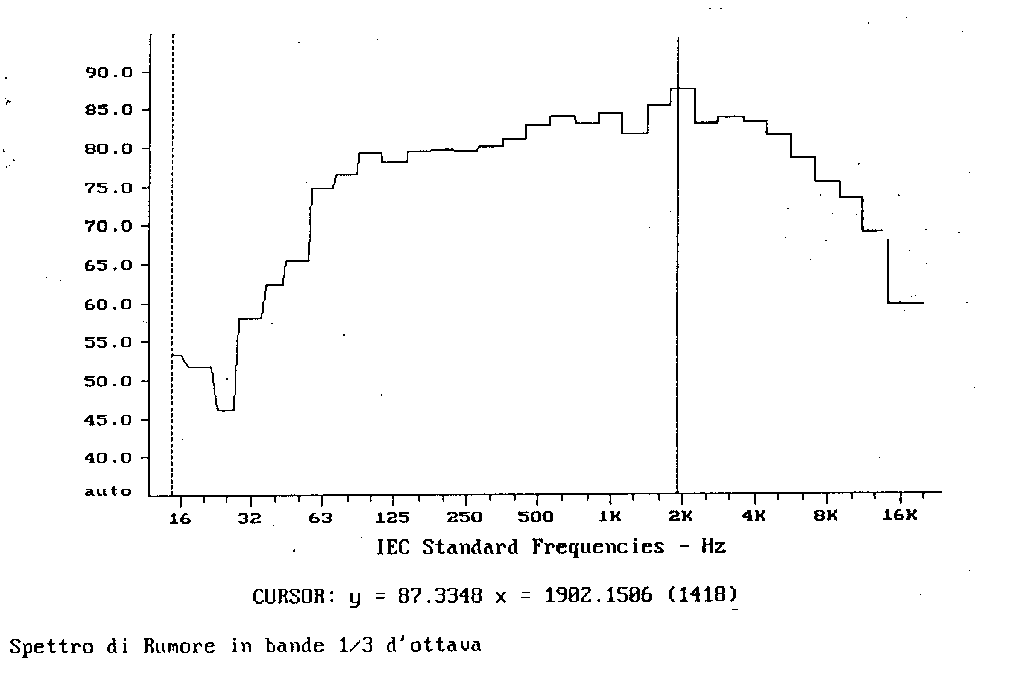
Fig.16
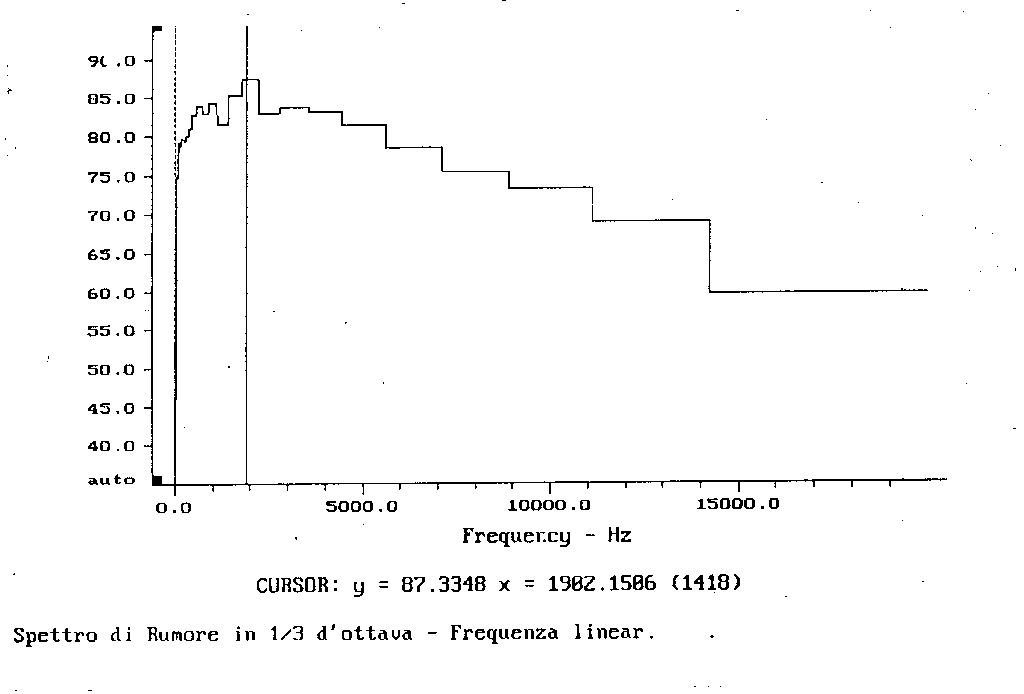
Fig. 17
Apparentemente i due spettri sono molto differenti, ma in realtà rappresentano sempre lo stesso segnale: si può vedere questo osservando il valore indicato dal cursore. In entrambi i casi si ha un picco di 87,3 dB alla frequenza di 1982,1286 Hz.
Passiamo ora dai filtri a banda percentuale costante a quelli a banda costante.
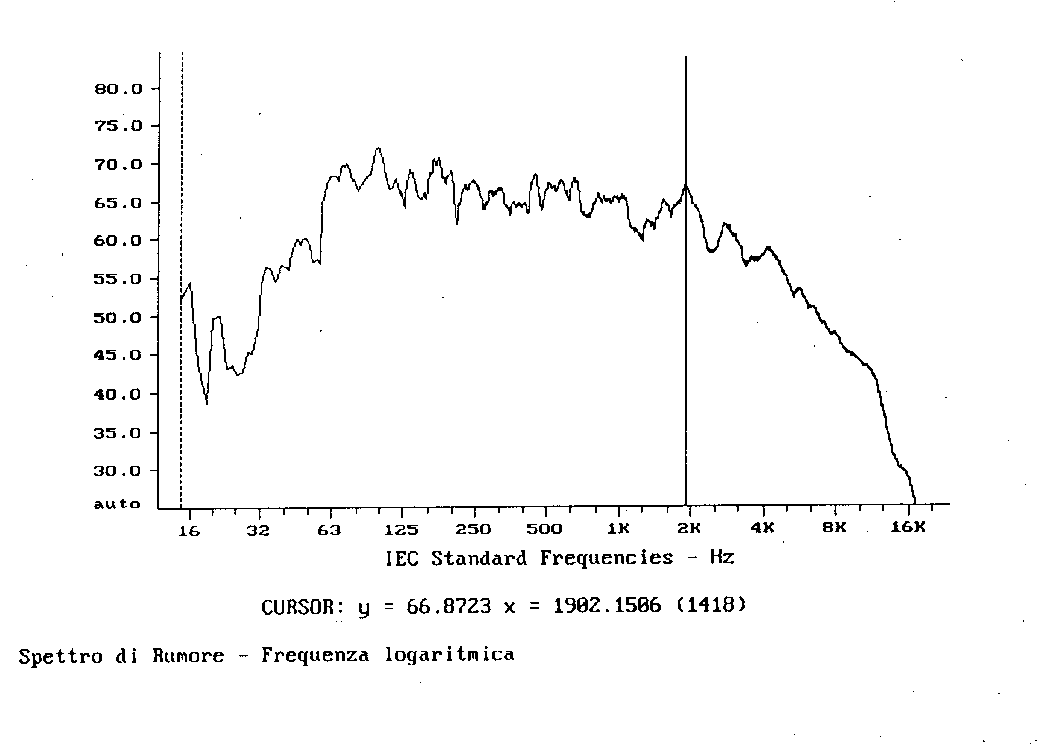
Fig. 18
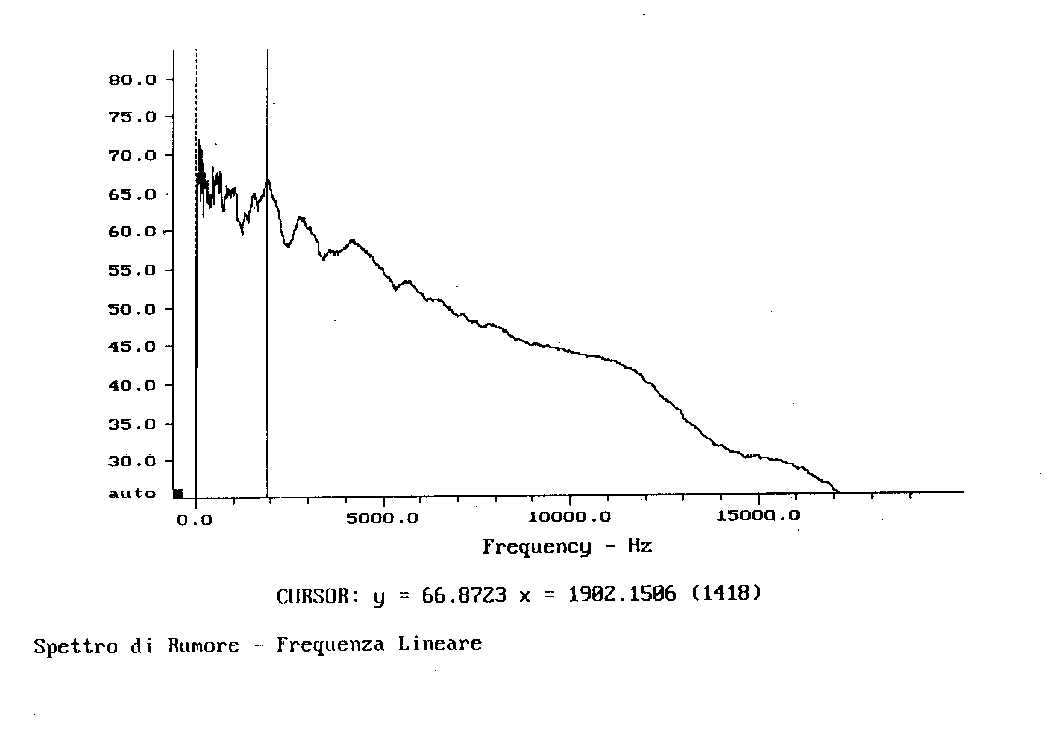
Fig. 19
Negli ultimi due casi, essendo le bande più strette, esse riescono a catturare frequenze ad un’energia mediamente inferiore a quella catturata dalla banda in terzi d’ottava. Normalmente, rispetto all’andamento in terzi d’ottava, un segnale visualizzato in banda stretta, tenderà ad attenuare i livelli ad alta frequenza ed ad incrementare quelli a bassa frequenza. Questo si può notare sia dalla fig. 18 sia dalla fig. 19.
Infine passando dall’analisi in terzi d’ottava alla banda stretta il valore in dB del segnale varia. Notiamo che a 2 kHz nei primi due grafici si otteneva un picco a 87,13 dB mentre negli ultimi due esso valeva 66,87 dB (circa 20 decibel di differenza).
Possiamo concludere con certezza che è necessario stabilire il tipo d’analisi in frequenza in quanto la scala tipografica della rappresentazione dello spettro ne può alterare notevolmente la lettura.
Resta comunque da sottolineare che il nostro udito è meglio rappresentato dall’analisi in terzi d’ottava con asse delle frequenze in scala logaritmica.