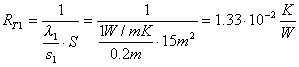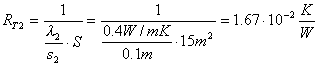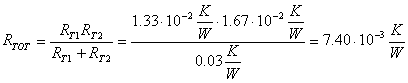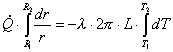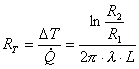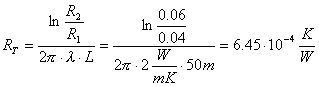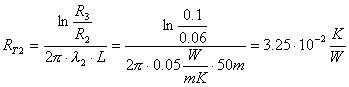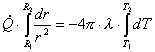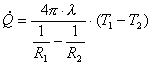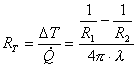TRASMISSIONE
DEL CALORE
Lezione del 5/12/2000
(ore 14:30-16:30) trascritta da Lorenzo Lazzari (matricola 124200)
Indice
Modalità di trasmissione
del calore
Applicazione:
lastra piana indefinita
Coefficiente
globale di scambio termico e Resistenza termica
Applicazioni:
strato cilindrico e sfera cava
Introduzione
In Termodinamica sono state definite due particolari forme di energia: il lavoro e il calore. Esse non sono funzioni di stato, ossia non sono caratteristiche dello stato del sistema, ma esistono solo quando il sistema è sede di uno scambio di energia (con altri sistemi, oppure al suo interno, o con l’ambiente circostante). Quando lo scambio di energia avviene in virtù di una differenza di temperatura si parla di trasmissione di calore; in tal caso, i Principi della Termodinamica ci permettono di affermare in primo luogo che il calore ceduto da un sistema deve essere uguale al calore ricevuto dall’altro (conservazione dell’energia) e che il calore viene trasferito spontaneamente dal sistema a temperatura maggiore a quello a temperatura minore.
Per citare un esempio, basti pensare a due corpi aventi temperature diverse che vengono posti a diretto contatto. Dopo un certo intervallo di tempo, essi raggiungono la medesima temperatura finale, compresa fra le due temperature a cui si trovavano inizialmente.
Con l’analisi termodinamica si può determinare la quantità di calore trasferito da un sistema all’altro senza alcuna informazione sul tempo impiegato dal processo, che solitamente avviene in tempi infinitamente lunghi, come nel caso del passaggio da uno stato di equilibrio all’altro. Nei problemi pratici, però, risulta necessario conoscere la rapidità del processo di scambio termico, a volte più ancora della quantità di calore trasferito. Nel dimensionamento di una caldaia, ad esempio, si deve conoscere in quanto tempo una determinata quantità di calore deve essere fornita, e non il valore numerico di questa; tant’è che parliamo di potenza della caldaia. Comunque, una volta nota la potenza termica scambiata, con una semplice operazione di integrazione possiamo determinare la quantità totale di calore trasferito in un dato intervallo di tempo.
Nella tecnologia moderna i processi di scambio termico hanno assunto un’importanza sempre maggiore. Tutti i componenti dei sistemi di generazione di potenza (dalle centrali termoelettriche ai motori delle automobili) implicano un trasferimento di calore da un mezzo all’altro. In campo ambientale i meccanismi di scambio termico hanno risvolti altrettanto rilevanti; basti pensare a quelli che regolano il clima, o a quelli che governano la trasmissione del calore di un edificio con l’ambiente circostante, di cui è fondamentale tenere conto durante la fase di progettazione dell’edificio stesso.
Modalità di trasmissione del calore
I processi di scambio termico sono generalmente classificati in tre categorie, anche se in pratica non si presenta mai una sola modalità, ma solitamente si ha la combinazione di almeno due di esse. Si tende però di solito ad individuare il tipo di scambio predominante, trascurando, a seconda di vari fattori (dei quali sicuramente molto rilevante è la temperatura), le altre modalità di trasmissione del calore presenti.
Le suddette tre categorie
sono: conduzione, convezione e irraggiamento.
La conduzione termica
è il processo che si attua in un mezzo solido, liquido o aeriforme nel momento
in cui, a causa di una differenza di temperatura, viene provocato un
trasferimento di energia cinetica da una molecola a quella adiacente che
possiede una velocità di vibrazione minore, essendo la velocità di vibrazione
delle particelle indice della temperatura del corpo. Si ha in questo modo un
trasferimento di energia, sotto l’influenza del gradiente di temperatura
(variazione della temperatura lungo una direzione), senza uno spostamento di
particelle; dunque il mezzo in cui avviene conduzione rimane nella condizione
di quiete.
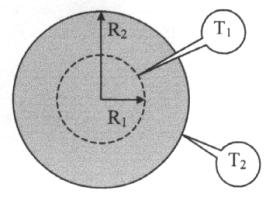
E’ il caso dell’esempio sopraccitato, in cui vengono messi a contatto due corpi inizialmente a temperature differenti T1 e T2, i quali, dopo un certo tempo in cui avviene conduzione termica, raggiungono la medesima temperatura T3 (fig. 1).

fig. 1
La convezione termica
avviene solamente in presenza di un fluido, ad esempio aria o acqua. Tale
fluido, a contatto con un corpo la cui temperatura è maggiore di quella
dell’ambiente che lo circonda, si riscalda e, per l’aumento di temperatura
subito, si espande (nella maggior parte dei casi). A causa della spinta di
Archimede, questo fluido sale, essendo meno denso del fluido circostante che è
più freddo. Contemporaneamente, il fluido più freddo scende e prende il posto
di quello più caldo che sale; in questo modo si instaura una circolazione
convettiva.
Per esempio supponiamo di
avere un sistema isolato dall’esterno costituito da due corpi aventi
temperature differenti, l’uno al di sopra dell’altro, divisi da uno strato di
acqua, che, come vedremo, svolgerà la funzione del sopraccitato fluido.
Supponendo che venga posto in superficie il corpo più freddo, siccome l’acqua
calda tende a salire a l’acqua fredda a scendere (per la diversa densità), si
sviluppa un moto convettivo per cui nella zona centrale l’acqua riscaldatasi a
contatto con il corpo caldo sale verso il corpo freddo, mentre nelle zone più
esterne si ha una movimento verso il basso dell’acqua che, raffreddatasi per il
contatto con il corpo freddo, si dirige verso quello caldo (fig. 2).
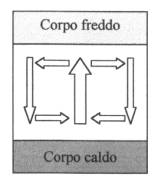
fig. 2
Si può osservare che si
avrebbe una situazione molto diversa nel caso in cui i due corpi venissero
invertiti, ossia se il corpo a temperatura maggiore fosse posto in superficie
ed il corpo a temperatura minore sotto lo strato d’acqua: in questo caso non si
avrebbe nessun moto convettivo, ma l’acqua rimarrebbe ferma trasferendo calore
dal corpo più caldo a quello più freddo solo per conduzione.
Si è fino ad ora descritta la convezione libera o naturale. La convezione può anche essere forzata, vale a dire che in alcuni casi, per scopi pratici, il moto del fluido può essere obbligato da ventole o pompe. Vi sono molteplici esempi pratici di convezione forzata, basti pensare alla caldaia di un termosifone che provoca la circolazione di un fluido, di solito acqua o aria, in modo da riscaldare le stanze della casa, oppure alla ventola atta a raffreddare la cpu di un computer.
Irraggiamento o radiazione termica è il termine usato per indicare la radiazione elettromagnetica emessa dalla superficie di un corpo che si trova ad una certa temperatura. Tutti gli oggetti emettono radiazioni elettromagnetiche, che sono frutto dell’eccitazione termica della superficie del corpo, legata alla condizione energetica dei suoi atomi (l’irraggiamento è tanto più intenso quanto maggiore è la temperatura dell’oggetto stesso), e viene emessa in tutte le direzioni; quando il mezzo trasmissivo risulta essere sufficientemente trasparente a tale radiazione, nel momento in cui essa colpisce un altro corpo, parte viene riflessa e parte assorbita. Tra i due corpi si stabilirà un continuo scambio di energia, con uno scambio netto di calore dal corpo più caldo al corpo più freddo.
Da notare è che può anche non esservi un mezzo di trasmissione, in quanto l’irraggiamento è l’unica modalità di scambio termico che avviene anche nel vuoto. Basti pensare alla radiazione solare, esempio più evidente di tale trasmissione.
Conduzione.
Legge di Fourier
Prima di scendere nel
particolare ed occuparci dettagliatamente della prima modalità di scambio termico,
la conduzione, è bene affermare che, in generale, lo scambio termico è un
fenomeno non lineare, non esiste cioè una semplice relazione di
linearità fra energia scambiata dai corpi coinvolti nel processo e temperature dei
corpi, tant’è che, ad esempio, in un fenomeno di irraggiamento il calore
scambiato è proporzionale alla quarta potenza delle temperature dei corpi.
Per studiare il trasferimento di calore si tende, sotto a sufficienti ipotesi, a linearizzare il fenomeno, introducendo equazioni dedotte talvolta dalla generalizzazione dei risultati sperimentali, come nel caso della legge di Fourier, che analizzeremo fra poco.
Tale semplificazione, come vedremo, verrà applicata a tutte e tre le metodologie di scambio termico, per ognuna delle quali esiste uno specifico coefficiente di proporzionalità fra energia scambiata e temperatura.
Come detto
nell’introduzione, quando si parla di scambio termico ciò che conta non è la quantità
di calore scambiato, ma la rapidità con cui avviene tale processo. In questo
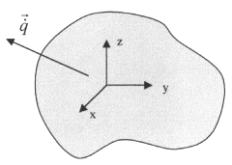
senso si introduce una grandezza vettoriale, detta flusso termico specifico
(oppure densità di flusso termico), che si indica con il simbolo ![]() . Le sue dimensioni sono:
. Le sue dimensioni sono:
![]() (1)
(1)
Essa rappresenta
l’energia che attraversa l’unità di superficie nell’unità di tempo, ed è
l’analogo della grandezza che in acustica è detta intensità I.
Per spiegare come il
vettore ![]() si orienta nello
spazio durante un processo di conduzione termica, consideriamo un solido
caratterizzato da una distribuzione di temperatura (campo termico) al tempo t data
da:
si orienta nello
spazio durante un processo di conduzione termica, consideriamo un solido
caratterizzato da una distribuzione di temperatura (campo termico) al tempo t data
da:
![]() (2)
(2)
fig. 3
In due dimensioni avremmo:
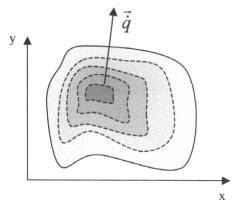
L’equazione (3), che esprime il postulato di Fourier, viene normalmente utilizzata nei problemi di trasmissione del calore per trovare un’espressione che descriva il campo termico in un corpo.
Tuttavia tale legge è
sufficiente solo se ci accontentiamo di una soluzione in regime stazionario,
ossia se eliminiamo la dipendenza dal tempo del campo termico del corpo, cosa
che faremo nelle successive applicazioni, evitando di ricorrere a equazioni
differenziali, spesso complicate.
Se invece viene richiesta
una soluzione in transitorio, ossia se si deve trovare la distribuzione delle
temperature in funzione del tempo, la legge di Fourier non è più sufficiente.
Solitamente la dinamica della conduzione viene descritta da una complessa
equazione differenziale del secondo ordine, detta equazione di Fourier,
che deriva direttamente dall’omonimo postulato.
Si può notare che
un’operazione equivalente è stata fatta in acustica quando si è dedotta
l’equazione di D’Alambert partendo dalla legge di Eulero, oppure, nella
fluidodinamica, ottenendo l’equazione di Navier dal postulato di Newton. La
differenza sta nel fatto che, mentre in questi due casi il passaggio dalla
legge fisica all’equazione non aveva risvolti pratici, l’equazione di Fourier
si rivela di fondamentale importanza nella risoluzione dei transitori termici .
Applicazione: lastra
piana indefinita
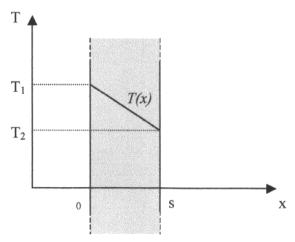
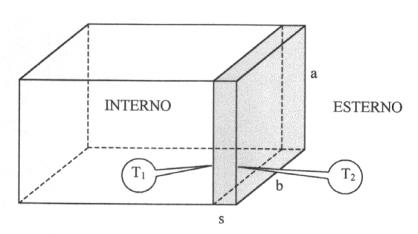
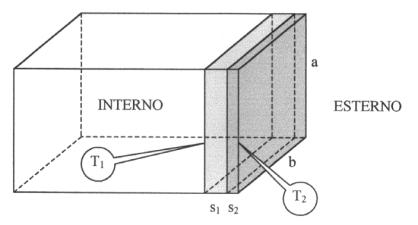
Il problema di conduzione
più semplice da risolvere è quello di una lastra di spessore s
infinitamente estesa nelle direzioni y e z (che rappresenta quindi un sistema
monodimensionale, dipendente solo dalla coordinata x), le cui facce sono
costantemente mantenute alle
temperature T1 e T2 (fig. 5). Il materiale
di cui è costituita ammette una conducibilità termica l costante. Si vogliono determinare il profilo
della temperatura all’interno della lastra T(x) (soluzione in regime
stazionario) e il flusso termico specifico ![]() fra le facce.
fra le facce.
Coefficiente
globale di scambio termico e Resistenza termica
Sulla base della supposta linearità fra flusso termico e temperatura generalizzata dalla legge di Fourier, vengono ora introdotte due particolari grandezze chiamate coefficiente globale di scambio termico e resistenza termica.
Il coefficiente globale di scambio termico,
che indichiamo con k, mette in relazione di proporzionalità diretta il
flusso termico specifico ![]() e la differenza di
temperatura DT:
e la differenza di
temperatura DT:
![]() (18)
(18)
In riferimento all’esempio appena trattato, ricordando l’equazione (13) che esprime il flusso termico specifico, ricaviamo il coefficiente globale di scambio termico di una parete:
![]() (19)
(19)
essendo s lo
spessore della parete e l la sua conducibilità termica.
Si può dunque esprimere
la potenza termica (o flusso termico) in funzione di k:
![]() (20)
(20)
dove S rappresenta
la superficie della parete.
Come nel caso del
coefficiente di conducibilità termica l, anche k, pur essendo un “coefficiente”,
non è un numero puro; le sue dimensioni sono:
![]() (21)
(21)
Da un punto di vista quantitativo, si può affermare che maggiore è il coefficiente k, maggiore è lo scambio termico. L’approccio al problema della conduzione tramite questo metodo è particolarmente usato nelle situazioni in cui si vuole massimizzare lo scambio termico.
Al contrario, quando si cercano soluzioni per minimizzare il flusso di calore, ossia quando si parla di isolamento, si preferisce utilizzare un altro coefficiente, detto resistenza termica.
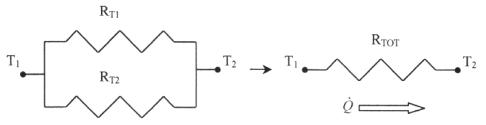
L’introduzione della resistenza termica, che
indichiamo con RT, si basa sull’analogia formale fra legge di
Fourier valida per la conduzione termica e la legge di Ohm che si applica ai
circuiti elettrici. In tal senso la grandezza RT svolge, nei
confronti del flusso termico ![]() e della differenza di
temperatura DT,
il medesimo ruolo che la resistenza elettrica R ha nei confronti
rispettivamente di corrente I e differenza di potenziale DV.
e della differenza di
temperatura DT,
il medesimo ruolo che la resistenza elettrica R ha nei confronti
rispettivamente di corrente I e differenza di potenziale DV.
Schematizzando la similitudine formale fra le due leggi si ha:
![]() (legge di
Fourier) «
(legge di
Fourier) « ![]() (legge di Ohm)
(22)
(legge di Ohm)
(22)
Ritornando all’esempio precedente, la resistenza termica di una parete avente conducibilità termica l ha espressione:
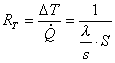 (23)
(23)
essendo s e S
rispettivamente lo spessore e la superficie della parete considerata.
Una differenza fra resistenza termica e resistenza elettrica sta nel fatto che, a differenza della seconda, che possiede una propria unità di misura detta Ohm (1W=1V/1A), la resistenza termica non possiede un’unità specifica, ma si misura in:
![]() (24)
(24)
L’inverso della
resistenza termica è detto conduttanza termica. Tale grandezza si indica
con il simbolo G e si misura in W/K:
![]() (25)
(25)
Applicazioni: strato cilindrico e sfera cava
Servendoci della legge di Fourier e del concetto di resistenza termica, andiamo ora a trattare due casi in cui la geometria si fa leggermente più complessa degli esempi già visti.
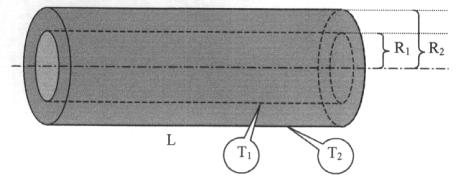
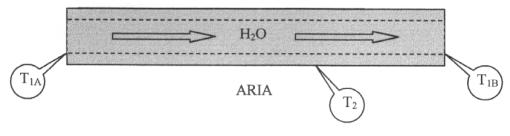
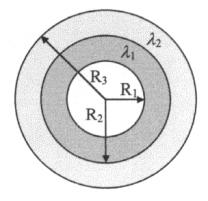
Consideriamo uno strato
cilindrico avente raggio interno R1, raggio esterno R2
e lunghezza L (fig. 11).
Appendice
Riporto in appendice una
tabella contenente i valori del coefficiente di conducibilità termica l alla temperatura di 20°C per alcuni materiali.
|
Acciaio |
52 |
|
Acciaio
inox |
17 |
|
Acqua
liquida in quiete |
0.60 |
|
Acqua
pesante da 10°C a 100°C |
0.56 ¸ 0.65 |
|
Alcool |
0.21 |
|
Alluminio |
220 |
|
Amianto |
0.113 |
|
Aria
secca in quiete |
0.026 |
|
Argento |
420 |
|
Asfalto |
0.698 |
|
Basalto |
1.27 ¸ 3.5 |
|
Bitumi |
0.17 |
|
Bronzo |
58 ¸ 65 |
|
Calcare
|
1.6 ¸ 3.5 |
|
Carbone |
0.14 ¸ 0.17 |
|
Carbone
in polvere |
0.12 |
|
Carta
e cartone |
0.14 ¸ 0.23 |
|
Cartongesso
in lastre |
0.21 |
|
Caucciù |
0.13 ¸ 0.23 |
|
Celluloide |
0.35 |
|
Cellulosa
compressa |
0.24 |
|
Cemento
in polvere |
0.07 |
|
Cenere |
0.069 |
|
Compensato |
0.109 |
|
Creta |
0.90 |
|
Dolomite |
1.8 |
|
Ferro
elettrolitico |
87 |
|
Gesso |
0.4 |
|
Ghiaccio
a 0°C |
2.22 |
|
Ghisa |
50 |
|
Glicerina |
0.220 |
|
Gomma
dura |
0.163 |
|
Grafite |
4.9 |
|
Granito |
3.18 ¸ 4.1 |
|
Intonaco
di calce e gesso |
0.70 |
|
Laterizi:
mattoni pieni, forati, leggeri |
0.25 ¸ 1 |
|
Lana |
0.038 |
|
Lava |
2.9 |
|
Leghe
di alluminio |
160 |
|
Legno
di abete |
0.12 |
|
Legno
di acero |
0.18 |
|
Legno
di quercia |
0.22 |
|
Manganina |
23 |
|
Marmo |
2.1 ¸ 3.5 |
|
Mercurio
liquido a 0° C |
8.13 |
|
Mercurio
liquido a 60° C |
9.64 |
|
Mercurio
liquido a 120° C |
10.92 |
|
Mercurio
liquido a 160° C |
11.6 |
|
Mercurio
liquido a 222° C |
12.78 |
|
Mica |
0.523 |
|
Neve
appena caduta fino a 3 cm |
0.06 |
|
Neve
soffice a strati da 3 a 7 cm |
0.12 |
|
Neve
moderatamente compatta da 7 a 10 cm |
0.23 |
|
Neve
compatta a strati da 20 a 40 cm |
0.7 |
|
Nichel |
58 ¸ 65 |
|
Oli e
petroli |
0.12 ¸ 0.17 |
|
Oro |
299 |
|
Ottone |
70 ¸ 116 |
|
Piombo
solido |
35 |
|
Platino |
70 |
|
Plexiglas |
0.157 |
|
Porcellana |
0.80 ¸ 1.05 |
|
Porfido |
2.9 |
|
Quarzo
^
all’asse |
6.6 |
|
Quarzo
parallelo all’asse |
12.8 |
|
Quarzo
oggetti fusi |
1.4 ¸ 1.9 |
|
Rame |
380 |
|
Sabbia
asciutta |
0.35 |
|
Sabbia
al 7% di umidità |
1.16 |
|
Sodio
solido |
125.60 |
|
Sodio
liquido da 100°C a 500° C |
86 ¸ 67 |
|
Stagno |
64 |
|
Steatite |
2.7 |
|
Sughero
di densità 200 Kg/m3 |
0.052 |
|
Tufo |
0.63 ¸ 1.7 |
|
Vetro |
0.5 ¸ 1 |
|
Zinco |
110 |
|
Zolfo |
0.23 |