In questo contesto parleremo del trasporto d'energia sotto forma di calore tra due o più corpi attraverso la trasmissione di onde elettro magnetiche, tale fenomeno è noto come irraggiamento.

L’irraggiamento differisce dalla conduzione e dalla convezione principalmente per il fatto che si manifesta anche senza la presenza di un mezzo trasmissivo. Perché ci sia irraggiamento è necessario che i corpi si "vedano", cioè tra essi sia presente un mezzo trasparente (anche il vuoto) che lasci passare l’onda elettro magnetica.

Consideriamo inizialmente aspetti di carattere generale osservabili fisicamente senza l’introduzione di grandezze specifiche.

Fig.1

Si considerino due corpi A e B attorno ai quali è stato creato il vuoto:

una certa quota di energia emessa dal corpo A finirà sul corpo B, viceversa una quota di energia emessa dal corpo B finirà sul corpo A. In generale le due quantità non saranno uguali e quindi avverrà uno scambio netto non nullo, nel senso che il calore fluirà da un corpo all’altro (secondo il principio zero della termodinamica dal più caldo al più freddo).

I corpi emettono indipendentemente dal fatto di " vederne altri", il corpo A non emette solo l’energia che finisce sul corpo B ma ne emette molta altra che si disperde nell’ambiente circostante ( analogamente per il corpo B), quindi si ha una emissione spontanea dei corpi che dipende dalla loro temperatura.

Un corpo è soggetto simultaneamente su ogni unità della sua superficie ad un flusso di energia irradiata uscente e ad uno entrante; il flusso uscente dipende dalla propria temperatura e quella entrante dalla temperatura dei corpi che irradiano.

Può accadere che nello stesso istante il corpo presenti una parte della sua superficie dove il bilancio è in attivo (prende più energia di quella che emette) e una parte dove il bilancio si chiude in passivo (emette più energia di quella che prende)

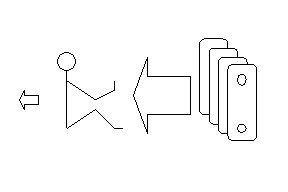
Fig. 2

Nella nostra trattazione considereremo casi semplici, nei quali il verso dell’irraggiamento è lo stesso su tutta la superficie e inoltre eviteremo di trattare corpi concavi, poiché una parte dell’energia emessa torma sul corpo stesso complicando ulteriormente la trattazione. 

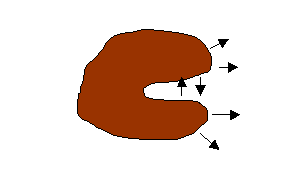
Fig.3 – Esempio di corpo concavo

Da queste prime osservazioni del fenomeno dell’irraggiamento possiamo affermare (in base al 1° principio della termodinamica) che se il corpo è in equilibrio termico con l’ambiente significa che esso irradia la stessa energia che assorbe, altrimenti non manterrebbe costante la sua temperatura.

Affinché si verifichi l’irraggiamento, ovvero abbia luogo il trasporto di energia è indispensabile che il campo elettrico, e il campo magneticoabbiano un comportamento oscillatorio.

L’irraggiamento di onde elettromagnetiche si può schematizzare graficamente attraverso due vettori ortogonali a se stessi ed alla direzione di propagazione denominati campo elettricoe campo magneticoche oscillano nel tempo sul proprio asse.

Nella figura numero 4 è rappresentato il caso più semplice nel quale i vettori dei due campi sono ortogonali fra di loro e variano nel tempo con una legge sinusoidale e sempre lungo la stessa direzione; in questo caso si parla di polarizzazione lineare dell’onda.

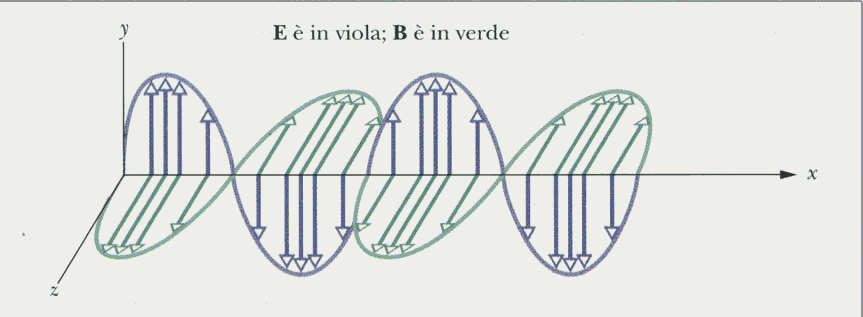
Fig. 4 – in questa rappresentazione vettoriale dell’onda elettromagnetica il vettore propagazione è diretto lungo x. Inoltre ricordiamo :

Nella figura si sono rappresentati i due campi in fase, condizione questa che massimizza il trasporto di energia da parte dell’onda elettromagnetica.

La velocità di propagazione è massima nel vuoto, dove il suo valore è quello della velocità della luce : .

[m/sec] ( 1 )

Se, invece, la propagazione avviene in un mezzo la velocità del fronte d’onda

(che indichiamo con ) dipende dal mezzo stesso attraverso il suo indice di rifrazione assoluto definito come:

. ( 2 )

Nella tabella riportata di seguito sono raccolti alcuni valori di indici di rifrazione assoluti per varie sostanze:

Tabella 1 – Valori misurati per pari a 589 nm (luce gialla )

Fino ad ora abbiamo considerato un’onda monocromatica, quella che in acustica chiamiamo un tono puro, una sinusoide ad una ben determinata frequenza.

Sono poche le sorgenti di radiazione elettromagnetica che emettono questo tipo di radiazioni, una delle quali è la lampada laser.

Gli altri corpi emettono simultaneamente su un ampio spettro di frequenze, compiendo una cosiddetta emissione in banda larga.

Nell’ambito della emissione di radiazioni luminose raramente lo spettro è continuo, è in banda larga ma presenta delle discontinuità.

Se andiamo ad analizzare l’energia totale emessa dal corpo in funzione della lunghezza d’onda, scopriamo che la stessa non è distribuita uniformemente, ma presenta un andamento irregolare nel quale si susseguono avvallamenti e cuspidi, anche molto selettive (fianchi stretti e ripidi).

Questo si vede bene per i gas, che sono molecole semplici, con atomi costituiti da pochi elettroni che presentano pochi stati eccitabili.

Quindi ammettono un'emissione di energia significativa solo per un ridotto numero di righe spettrali.

L’idrogeno, per esempio, presenta un solo elettrone che può assumere un numero ridotto di stati eccitati che, quando abbandona per portarsi ad una condizione di minore energia, emette un fotone la cui frequenza è funzione dell’orbitale di partenza e di arrivo secondo la legge della fisica quantistica:

( 3 )

dove h è la costante di Planck e vale  

Proprio per il ridotto numero di combinazioni le righe spettrali di questo gas sono 5.

Fig. 5 – Spettro di emissione dell’idrogeno nelle frequenze del visibile 

Per sostanze più complesse, che presentano più atomi e magari con un elevato numero di elettroni l’analisi spettrale dell’energia emessa ha un aspetto quasi continuo e non più quello di un oscillatore che ha frequenze ben precise.

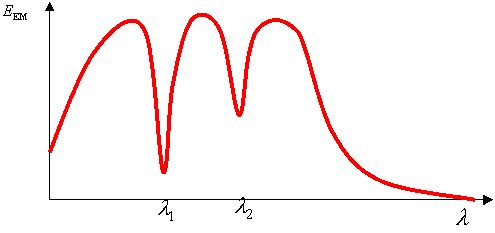
Fig. 5 – Generico spettro di emissione per un materiale complesso

In analogia con l’acustica consideriamo una lastra di materiale semitrasparente sulla quale facciamo incidere una luce bianca, avvero con un'energia distribuita equamente su tutte le frequenze( non solo nel campo del visibile ), come mostra il disegno avremo una intensità incidente, una riflessa, nonché una intensità assorbita e una trasmessa.

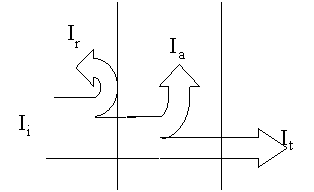
Fig. 6

Andando a studiare lo spettro dell’energia di questa ultima componente ( quella trasmessa ) notiamo la presenza di bande di assorbimento, la alle stesse frequenza che caratterizzavano lo spettro di emissione del materiale attraversato. 

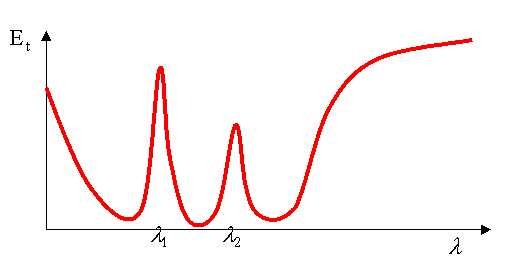
Fig. 7 – spettro di trasmissione normalizzato relativo allo stesso materiale di Fig.5

Siamo di fronte ad un fenomeno simmetrico: l’elettrone che da uno stato eccitato si porta in una condizione di minore energia emette un fotone ad una determinata lunghezza d’onda, ma nel momento in cui sotto l’azione di una luce bianca è eccitato assorbe un fotone alla stessa frequenza, caratteristica della particolare transizione.

Il campo di frequenze delle onde elettromagnetiche occupa un ampio spettro che si estende dai raggi gamma alle onde lunghe, la cui suddivisione interna è rappresentata nello schema sotto. 

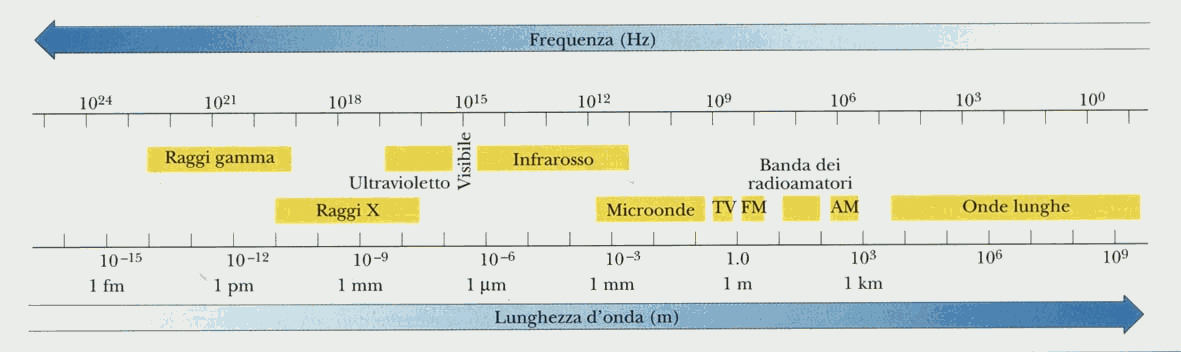
Fig. 8 – Si noti che le scale utilizzate nella rappresentazione sono di tipo logaritmico.

Si può definire operativamente la luce visibile come quella radiazione elettromagnetica a cui l’occhio è sensibile. La sensibilità di osservatori individuali può variare, ma tipicamente l’uomo è in grado di vedere la radiazione nell’intervallo di frequenze d’onda che va da 400nm a 700nm (che corrisponde all’intervallo di frequenze che va da a Hz ).

All’interno di questo intervallo la sensibilità a differenti lunghezze non è affatto costante. La figura 9 riporta una rappresentazione della variazione della sensibilità di un osservatore standard a radiazioni di differente lunghezza d’onda ma di uguale intensità sulla regione visibile dello spettro. 

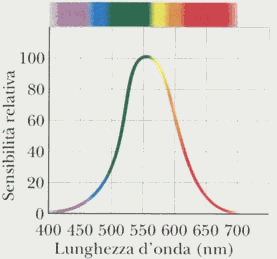
Fig. 9

La massima sensibilità si ha nei dintorni di 555nm, che corrisponde ad una lunghezza di colore giallo-verde.

Sotto l’aspetto del trasporto energetico nessuna frequenza è trascurabile, ma per applicazioni terrestri, il campo di frequenze che interessana il nostro studio si estende dall’estremo superiore della radiazione solare (ultra violetto) fino alle onde radio (da 0,4 nm a qualche millimetro delle microonde). Escludiamo quindi le radiazioni ionizzanti ( raggi x, raggi gamma) che per i tessuti cellulari sono teratogene, cancerogene.

Dal punto di vista tecnico il settore che ci interessa di più è quello degli infrarossi poiché in esso spontaneamente i corpi emettono la maggior parte dell’energia.

Definizione fondamentale delle grandezze 

Definiamo la potenza emessa per metro quadro di superficie che indichiamo con il simbolo ‘’ e, la cui unità di misura è il Watt su metro quadrato.

( 4 )

Nel campo delle scienze radianti questa grandezza si chiama

potere emissivo integrale (o densità di flusso termico), è una quantità sempre positiva ed è indipendente dalla radiazione incidente sul corpo.

Il valore di dipende solo dallo stato superficiale del corpo e dalla sua temperatura( vedremo in seguito in che modo).

Altra grandezza definita nello studio delle scienze radianti è il potere emissivo specifico (o monocromatico)

( 5 )

riferito all’unità di lunghezza d’onda, la cui unità di misura è .

In funzione di questa grandezza posso definire il potere emissivo integrale come, appunto, integrale su tutte le lunghezze d’onda, ognuna con il suo contributo di flusso termico.

( 6 )

Si può notare che un corpo, oltre ad irradiare una certa , riflette una quantità di radiazione ricevuta , dopo averne assorbita una quantità ed eventualmente trasmessa una quantità .

La irradiata è molto piccola, o addirittura al di fuori del campo visibile stesso. È per questo che i colori dei corpi a temperatura ambiente, per come percepiti dall’occhio umano, dipendono soprattutto dalla riflessa. Solo alle alte temperature la irradiata inizia a diventare rilevante ed i corpi si colorano a partire dal rosso.

Partendo dalla semplice relazione:

 ( 7 )

dividendo membro a membro per :

( 8 )

e definendo:

( 9 )

rispettivamente come coefficienti di assorbimento, di riflessione e di trasmissione.

Un corpo che non si lascia attraversare da onde elettromagnetiche ( per il quale si ha quindi t=0 ) si definisce opaco. Quasi tutti i materiali solidi di spessore superiore a quello dello strato superficiale vengono considerati opachi ( nel campo delle radiazioni prese in esame ), quindi l’equazione precedente si riduce a:

( 10 )

Il coefficiente di assorbimento a (come r e t ) dipende oltre che dallo stato superficiale del corpo, dalla lunghezza d’onda e dalla temperatura T.

Naturalmente per il modo in cui è stato definito, a può assumere tutti e soli i valori compresi tra 0 e 1. 

Ai fini della comprensione dell’irraggiamento è necessario introdurre due concetti fisici che rispondono al nome di corpo nero e corpo grigio

Il corpo nero è un oggetto in grado di assorbire tutta l’energia incidente indipendentemente dalla lunghezza d’onda( a=1 , T ).

Per definizione il corpo nero ha un'energia riflessa uguale a zero ed è opaco.

Tali condizioni si realizzano considerando un corpo isotermo e cavo, la cui cavità è di materiale con elevato coefficiente di assorbimento ed in contatto con l’esterno tramite un minuscolo foro.

Se un raggio di luce entra nella cavità, colpendo la superficie interna, viene in parte assorbito ed in parte riflesso, perdendo una grossa percentuale d’energia ad ogni riflessione.

Fig. 10-Possibile sezione di un corpo nero 

Siccome il raggio di luce prima di poter eventualmente uscire dalla cavità deve compiere molte riflessioni, questo viene completamente "catturato" dalla cavità o, se riesce ad uscirne, n’esce con un’energia trascurabile.

La superficie proiettata dal foro sul piano tangente al corpo in corrispondenza del foro stesso, si comporta quindi con buon’approssimazione, come un corpo nero nei confronti della radiazione incidente.

D’ora in poi tutte le grandezze riferite ad un corpo nero, avranno pedice zero. 

Poiché il corpo nero ha coefficiente di assorbimento massimo per tutte le frequenze, anche la sua emissione è massima ad ogni frequenza (lo dimostreremo in seguito). 

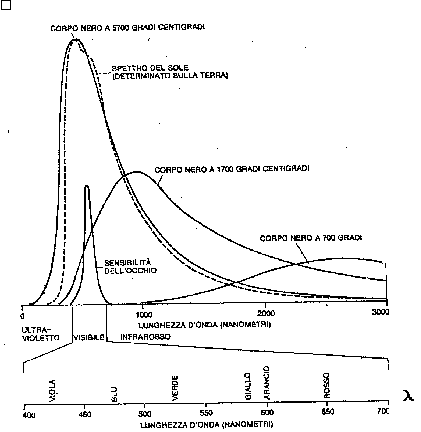
Fig.11 – Spettro di emissione del corpo nero a diverse temperature.

L’asse delle ordinate esprime il valore di e .

Lo spettro di emissione del corpo nero è stato quindi disegnato fenomenologicamente come inviluppo delle punte degli spettri di emissione dei corpi reali, ma è possibile, appoggiandosi alla fisica quantistica, determinare l’espressione analitica del potere emissivo monocromatico attraverso la legge di Planck

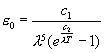( 11 )

nella quale:

= (prima costante di Planck )

( seconda costante di Planck )

E’ necessario a questo punto raccogliere qui di seguito le leggi che regolano il fenomeno ‘corpo nero’ poiché pur essendo state formulate precedentemente la legge di Planck, possono comunque essere ricavate da quest’ultima.

Analizzando l’espressione ( 11 ) risulta evidente la dipendenza di da e da T e, come si può notare osservando la Fig. 11 all’aumentare della temperatura del corpo nero la curva si ‘alza’, mentre il valore massimo della stessa si porta verso lunghezze d’onda minori.

Per elevate temperature il corpo nero può arrivare ad avere il massimo valore di all’interno dello spettro visibile.

Attraverso lo stesso meccanismo i corpi non neri se riscaldati cominciano ad emettere luce rossa e a mano a mano che la loro temperatura viene innalzata cominciano a diffondere luce che l’occhio percepisce come bianca.

La legge di Wien ci permette di calcolare la lunghezza d’onda alla quale corrisponde il massimo di (,T).

Deriviamo l’espressione della legge di Planck:

( 12 )

la quale in corrispondenza del valore massimo di si deve annullare.

Essendo e diversi da zero si ottiene:

( 13 )

dalla risoluzione della quale si ricava la legge di Wien:

( 14 )

Osservando questa legge si può affermare che il grafico di in funzione di T è un ramo di iperbole, quindi all’aumentare del valore della temperatura il valore massimo arretra verso lunghezze d’onda minori.

La funzione che lega il potere emissivo integrale del corpo nero alla sua temperatura ( alla quarta ) è nota come legge di Stefan-Boltzmann, ed è data da:

( 15 )

dove

( 16 )

ricavata dalla termodinamica quantistica, è detta costante di Stefan-Boltzmann.

La legge espressa dalla formula ( 15 ) si ricava per via analitica attraverso la legge di Planck.

( 17 )

La legge di Prevost afferma che la potenza scambiata ( ) è quella emessa

( ) meno quella ricevuta ( ):

( 18 )

ovviamente tale legge ha carattere generale, non è valida solo per il corpo nero.

Poiché il corpo nero è un'astrazione fisica, il modello più vicino alla realtà è il corpo grigio la cui caratteristica è quella di avere il coefficiente a < 1, ma costante. In generale per gli altri corpi non grigi, il coefficiente di assorbimento è funzione di e di T:

la dipendenza da è evidente poiché abbiamo già visto che lo spettro di assorbimento dei materiali in generale dipende da ; quindi per il modo stesso in cui è stata definito a (formula 9 ), anche il coefficiente di assorbimento dipenderà dalla stessa grandezza. La dipendenza della temperatura si può comprendere osservando che lo stesso materiale a temperature più alte avrà elettroni che alternano il loro stato tra orbitali ad energia maggiore poiché già l’energia del sistema è di per se più alta essendo più alta la temperatura.

Se il corpo è a temperatura elevata gli elettroni sono già eccitati ai livelli più bassi e quindi le transizioni avvengono tra stati ad energia maggiore.

Per corpi costituiti da un certo numero di sostanze o da atomi molto complessi il comportamento emissivo si avvicina maggiormente a quello del corpo nero, o meglio una coppia scalata di esso.

Il corpo grigio è un corpo nero ridotto (corpo nero che assorbe di meno e emette meno).

Il modello di corpo grigio è importante anche se nella realtà i corpi non sono grigi, ma sostanze chimiche complesse possono avvicinare il comportamento ideale del corpo nero (in modo qualitativo) pur evidenziando un rapporto /< 1; quindi molto più vicine al modello di corpo grigio. 

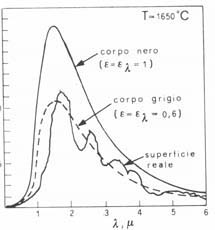
Fig. 12 - confronto di potere emissivo del corpo nero e di un corpo grigio con quello di una superficie reale.

Risulta molto importante a questo ponto sottolineare che il rapporto tra l’energia emessa dal corpo grigio e quella emessa dal corpo nero è uguale al rapporto tra quella assorbita dal corpo grigio e quella assorbita dal corpo nero. 

Indichiamo e il rapporto tra il potere emissivo del corpo grigio e quello del corpo nero.

( 19 )

oppure:

( 20 )

per la quale è data per scontata l’invarianza rispetto alla lunghezza d’onda.

La proprietà enunciata non è banale in quanto si mettono a confronto il fenomeno di ricezione e di emissione che sono apparentemente indipendenti.

La dimostrazione di questo fatto si compie con un semplice esperimento:

si pone un corpo nero in una cavità mantenuta a temperatura T1 e dopo un certo tempo il corpo e la cavità saranno alla stessa temperatura.

Evidentemente, a regime, la potenza emessa e la potenza incidente sul corpo nero coincidono.

= ( 21 )

La potenza incidente è completamente assorbita dal corpo nero, mentre quella emessa è irraggiata tutta all’esterno poiché si è escluso che il corpo sia convesso.

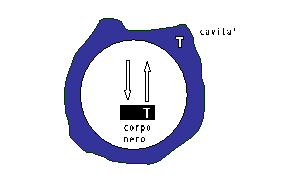
Fig. 13

Ripetiamo l’esperimento con un corpo grigio: la potenza emessa, per definizione, vale

= e ( 22 )

mentre la potenza assorbita vale

= a ( 23 )

La potenza incidente è uguale alla potenza emessa nel corpo nero ( 21 ); a regime quella incidente il corpo grigio deve essere uguale a quella emessa altrimenti il sistema non si manterrebbe in equilibrio termico (contro il primo principio della termodinamica); ne consegue

a = e ( 24 )

Da ciò si deduce che il corpo nero non soltanto è il corpo che assorbe maggiormente energia, ma è anche quello che ne irradia maggiormente.

Attraverso la legge di Planck e le sue derivate possiamo conoscere quanta energia viene emessa dal corpo per una determinata lunghezza d’onda ma non abbiamo alcuna informazione di come questa venga distribuita nello spazio.

Per rispondere a questa domanda introduciamo una nuova grandezza che chiamiamo potere emissivo angolare.

Si consideri una parte della superficie del nostro corpo emittente sulla quale evidenziamo un punto D. Sia P un punto scelto arbitrariamente nello spazio circostante e indichiamo con r la semiretta congiungente i due punti e con l’angolo che forma questa con l'ortogonale alla superficie nel punto D.

Chiamiamo ds la superficie infinitesima attorno al punto P.

Se ora indichiamo con l’angolo solido centrato sulla retta r attraverso cui il punto D vede la mia superficie ds possiamo definire una nuova grandezza che chiameremo potere emissivo angolare la cui espressione risulta:

( 25 )

Tale grandezza indica la parte di potere emissivo che esce attraverso l’angolo solido considerato nell’unità di tempo.

Il potere emissivo angolare è funzione del solo angolo , questa caratteristica ci permette di affrontare un problema tipicamente tridimensionale in modo bidimensionale.

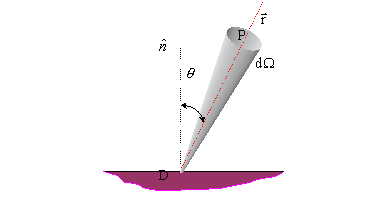
Fig.14 

Dalla definizione di i, si deduce che per una sorgente puntiforme:

, ( 26 )

e per una sorgente estesa che vede solo un semispazio:

. ( 27 )

Tracciamo quindi un diagramma rappresentativo del potere emissivo angolare:

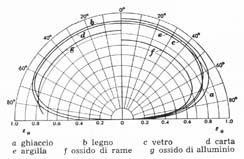
Fig.15 – curve iso-emissione, congiungono tutti i punti a uguale  

Per gli apparecchi di illuminazione queste rappresentazioni grafiche vengono denominate solidi fotometrici.

Nel caso delle lampade viste come assieme e non come superficie piana indefinita, o per superfici levigate a specchio il solido fotometrico può avere uno sviluppo non rotazional-simmetrico, cioè con solidi fotometrici fortemente diversi lungo l’asse longitudinale e l’asse trasversale.

Per il corpo nero si enuncia una legge di emissione relativamente semplice che prende il nome di legge di Lambert:

una superficie di grandi dimensioni, vasta rispetto alle dimensioni delle lunghezze d’onda incidenti e con le caratteristiche di un corpo nero presenta un'emissione che indichiamo con:

= ( 28)

Che è uguale al valore massimo nella direzione normale per il coseno di .La legge si chiama anche del coseno.

Il diagramma del solido fotometrico (come si può osservare dalla Fig. 15 ) disegnato nel rispetto della legge suddetta ha la forma di una sfera.

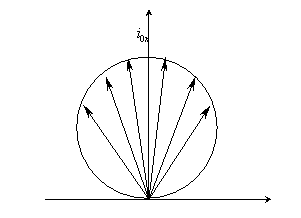
Fig. 16

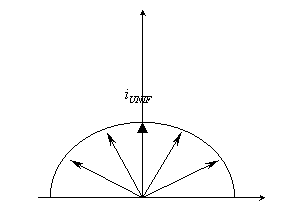
Fig. 17

Rispetto ad una ipotetica emissione uniforme, spesso utilizzata per rappresentare l’emissione di corpi non neri (a semisfera) il valore in direzione normale dell’emissione di Lambert deve essere doppio di quella uniforme a parità di potere emissivo integrale.

( 29 )

L’ipotesi di Lambert è ottima per l’illuminotecnica poiché ci permette di rappresentare con buona approssimazione gli andamenti reali rilevati sperimentalmente; mentre l’emissione uniforme è quella che meglio rappresenta l’emissione sonora

Naturalmente tutta la trattazione sulla emissione angolare del corpo nero viene estesa al corpo grigio, per il quale le relazioni che abbiamo scritto dovranno essere corrette con un fattore di riduzione (= a ).

Introduciamo quindi il concetto di "grigezza" per l’emissione spaziale; in altre parole il diagramma risulterà di forma uguale a quella per un corpo nero ma con valori ridotti rispetto al primo

L’intensità è una grandezza valutata nell’ottica di chi riceve, in illuminotecnica di chi vede. È definita mettendo l’occhio dell’osservatore in corrispondenza di un ben preciso angolo . L’occhio vede una superficie emittente apparente che è la proiezione sul piano normale all’angolo di osservazione e che quindi risulta ridotta di rispetto alla effettiva dimensione.

La superficie apparente è così sempre più piccola di quella reale, solo nel caso in cui sia zero gradi le due dimensioni coincidono.

L’intensità è dunque potenza diviso superficie apparente e si indica come

( 30 )

la particolare definizione di questa nuova grandezza fa si che l’intensità di radiazione di un corpo nero sia costante per qualunque valore di :

aumentando il valore di l’emissione della superficie diminuisce di un fattore, ma anche la superficie apparente cala secondo la stessa legge; il rapporto quindi resta invariato al variare dell’angolo di osservazione.

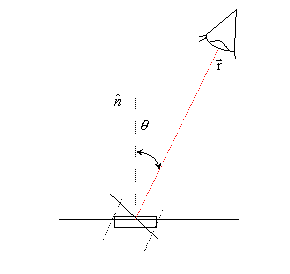
Fig. 18