IL 2° PRINCIPIO DELLA TERMODINAMICA
INTRODUZIONE
Molti anni fa, nel 18° secolo, si pensava che la trasmissione del calore tra i corpi fosse possibile grazie ad un fluido materiale detto CALORICO che riusciva ad essere scambiato tra corpi a contatto e a temperature diverse tra loro. Il corpo più caldo conteneva una quantità maggiore di calorico rispetto al corpo più freddo e quindi era in grado di cederlo a quest’ultimo, per mantenere l’equilibrio termico. Con l’introduzione del 1° Principio della Termodinamica, il calore viene ad essere considerato una vera e propria forma di energia. Decade così il concetto di calorico che viene ad essere inadeguato alla nuova concezione : I corpi a contatto si scambiano energia.
Il 2° Principio della Termodinamica tende inoltre a smentire, o meglio a ridimensionare alcune delle considerazioni che si possono fare valutando il 1° Principio della Termodinamica. Infatti, secondo quest’ultimo, sarebbe possibile convertire il calore in lavoro :
U2 - U1 = Q - L
dove :
- U2 = Energia interna finale
- U1 = Energia interna iniziale
- Q = Quantità di calore scambiata (da considerare positiva se assorbita dal sistema) con l’esterno del sistema
- L = Lavoro scambiato (da considerarsi positivo se prodotto dal sistema verso l’esterno) con l’esterno del sistema
Quindi tenendo anche presente la variazione dell’energia interna del sistema, risulta proprio possibile trasformare il calore in lavoro e viceversa.
In un senso, e cioè LAVORO à CALORE, il processo può avvenire tranquillamente, basti pensare al fatto che la forza applicata per produrre lavoro su un corpo mobile può essere contrastata dall’attrito interno al sistema che provoca calore (anche se in questo caso è dannoso perché limita l’effetto del lavoro stesso).
Nell’altro senso invece, le cose si complicano.
Il 2° Principio quindi tende a smentire chiunque pensa che le varie forme di energia siano tra loro mutuabili senza limitazioni.
Se fosse possibile convertire, in un modo tecnologicamente agevole, il calore in lavoro, avremmo la possibilità di avere quasi "gratuitamente" enormi quantità di energia da poter sfruttare come vogliamo. Infatti il calore è una delle forme di energia che più si "sviluppa" e si accumula nei vari processi che avvengono quotidianamente.
Bisogna considerare che le varie forme di energia si possono raggruppare in due classi principali :
CLASSE A (Nobili) :
- energia elettrica
- energia meccanica
- energia chimica
- ...
CLASSE B (Meno mutuabili)
- calore
- alcune forme di energia chimica (ad esempio quelle non direttamente trasformabili in energia elettrica)
- ...
La differenza sostanziale, che dà importanza a questa classificazione, sta nel fatto che le energie di classe A sono trasformabili con alti rendimenti per i processi di trasformazione che vanno verso B, mentre quelle di classe B, pur ammettendo che sia possibile trasformarle in classe A non garantirebbero una convenienza tale da giustificarne la conversione, in quanto i rendimenti per i processi B à A sono molto bassi. Quindi :
Aà B : Sono possibili quasi integralmente, con rendimenti prossimi a 1
Bà A : Sono processi impediti a meno di accontentarsi di grosse perdite di energia a causa di rendimenti molto bassi.
I processi che riguardano le trasformazioni possibili tra le energie di classe A sono quindi "convenienti" dal punto di vista delle perdite.
Ad es :
passando da Energia Chimica ad Energia Meccanica le perdite sono trascurabili e sono limitabili a seconda di come costruiamo il sistema e quindi a seconda della nostra accortezza verso l’eliminazione di quelle componenti fastidiose che provocano perdite (come ad esempio l’attrito).
Cioè non c’è alcun limite fisico che impedisce di pensare di abbassare questo fattore di perdita.
Consideriamo invece un improbabile processo di trasformazione calore à lavoro :
Prendiamo un contenitore riempito con 100 l di acqua calda a 100 °C posto in un ambiente a temperatura di 20 °C. Se proviamo a calcolare quanto calore può cedere questo sistema otteniamo che :
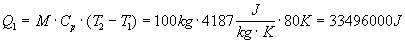
Questa è di per se una quantità di energia enorme che potrebbe essere sfruttata ad esempio per alimentare un’automobile per moltissimo tempo. Il sistema riesce a cedere calore verso l’ambiente esterno abbassando la propria temperatura, cioè raffreddandosi fino alla temperatura dell’ambiente (20 °C) alla quale trova l’equilibrio.
Cioè diminuisce, man mano che la temperatura si abbassa, la capacità del sistema di fornire calore. Graficamente troviamo :
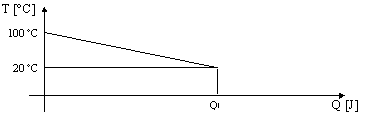
Figura 1
In realtà proprio il secondo principio mi fornisce un limite importante dovuto al rendimento basso che si ha in una eventuale trasformazione del calore sopra analizzato (la trasformazione è ovviamente Calore à Lavoro).
Forniamo ora alcune definizioni indispensabili per la trattazione degli altri argomenti.
ANERGIA ed EXERGIA
Considerando un sistema stabile con una certa energia totale E, questa si può suddividere in due importanti categorie :

Figura 2 - Differenze tra ANERGIA ed EXERGIA
Cioè se ad esempio immaginiamo di convertire calore in lavoro, soltanto l’exergia sarà effettivamente mutuata in lavoro. E purtroppo questa è una piccola parte di E (che è l’energia totale).
Alcuni filosofi moderni hanno addirittura definito Exergia = Energia buona e Anergia = Energia cattiva, anche se questa definizione è sbagliata perché non è detto che l’Anergia sia sempre dannosa e che l’Exergia sia utile. Non bisogna quindi dedicarsi soltanto alla conservazione di Exergia o a rendere l’Exergia maggiore possibile, perché nelle varie applicazioni possono essere utili entrambi.
Un esempio di "distruzione" dell’Exergia può essere:
Consideriamo una pila elettrica che deve alimentare una resistenza per produrre calore.
L’energia chimica della pila è nobile, di classe A, e può essere trasformata in energia elettrica, anch’essa di classe A. Se alimento una resistenza finisco per avere una dissipazione completa per effetto Joule in calore. Sono partito dall’avere un sistema con una Etotale composta in prevalenza da Exergia e sono arrivato alla fine ad avere distrutto l’Exergia e aver prodotto Anergia in quantità pari all’Exergia distrutta (ricordiamo che l’energia totale rimane la stessa).

Figura 3 - Perdita di Exergia
Ma allora si capisce immediatamente che questo procedimento è assolutamente poco astuto. Si poteva infatti ottenere lo stesso risultato sfruttando anziché un’energia di partenza di classe A, una di tipo B come ad esempio un’energia chimica derivante dalla combustione di carbone. Il rendimento di questo nuovo processo sarebbe stato comunque decisamente prossimo ad 1 con il vantaggio di non aver sprecato un’energia così importante come l’Exergia.
Introduciamo ora due importanti definizioni che ci condurranno verso le formulazioni del 2° Principio della Termodinamica.
SERBATOIO
È un sistema chiuso che idealmente riesce a scambiare quantità di calore Q (positivo o negativo a seconda se è rispettivamente assorbito o ceduto verso l’esterno) più o meno grandi a piacere con l’ambiente esterno mantenendo comunque la propria temperatura costante.
I serbatoi di calore in realtà non si può dire se esistono oppure no se non si cerca di stabilire cosa voglia dire "quantità di calore più o meno grandi a piacere". Infatti è inimmaginabile che la temperatura di un serbatoio rimanga costante se scambia una grandissima quantità di calore, almeno ragionando nella realtà fisica del problema.
Un esempio di serbatoio di calore può essere un serbatoio contenente acqua e ghiaccio. Questo infatti è ad una temperatura di equilibrio per la quale l’acqua e il ghiaccio sono a temperatura di 0 °C. Se proviamo a prelevare calore, vediamo che un po’ di ghiaccio si forma, mentre se proviamo a fornire calore, vediamo che un po’ di ghiaccio si fonde. I processi che possono avvenire nei due casi riescono quindi a mantenere la temperatura costantemente a 0 °C.
Un altro esempio può essere l’ambiente. Quando preleviamo o forniamo calore all’ambiente, la sua temperatura rimane costante (ad esempio a 20 °C). Al massimo si può accettare il fatto che localmente si verificano dei piccoli sbalzi di temperatura, ma complessivamente il sistema ambiente è talmente grande che questi sbalzi sono ininfluenti alla sua temperatura.
MACCHINA CICLICA
È una macchina a fluido normalmente tipo :
- una pompa per la bicicletta
- motore a scoppio
- un motore diesel
- locomotiva a vapore
- caldaia a vapore
- ...
Sono macchine che al termine del processo di produzione del lavoro tornano allo stato di fisico di partenza. Al termine del ciclo risulta quindi che la loro variazione di energia interna è nulla :
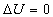
Possono essere sistemi aperti o chiusi. Ad esempio il motore a combustione interna è un sistema aperto, mentre invece la macchina a vapore è un sistema chiuso.
Normalmente le macchine cicliche sono formate da :
- 1 serbatoio caldo a temperatura T1
- 1 serbatoio freddo a temperatura T2 (quindi con T2<T1)
Lo schema classico della macchina è :
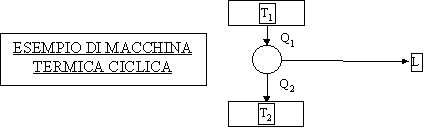
Figura 4
Ora è possibile fornire gli enunciati del 2° Principio della Termodinamica :
ENUNCIATO di KELVIN - PLANCK del 2° PRINCIPIO DELLA TERMODINAMICA
Non è possibile costruire una macchina termica in grado di effettuare una trasformazione il cui unico risultato sia la conversione di Calore in Lavoro.
Quindi non è possibile costruire una macchina termica che non dissipi calore Q2 verso il serbatoio più freddo e che quindi lavori con il solo serbatoio caldo:
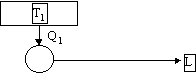
Figura 5
ENUNCIATO di CLAUSIUS del 2° PRINCIPIO DELLA TERMODINAMICA
Non è possibile costruire una macchina termica il cui unico risultato sia quello di trasferire calore da un serbatoio più freddo ad uno più caldo.
Quindi non è possibile costruire una macchina termica del tipo :
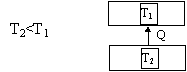
Figura 6
Apparentemente l’ultimo enunciato visto può apparire distante dal primo. In realtà entrambi vogliono dire la stessa cosa ma da due punti di vista differenti. Infatti se supponiamo falso uno dei due, riusciamo ad impostare un ragionamento che ci porta a negare anche l’altro.
Dimostriamo quindi che il primo enunciato e il secondo vogliono dire la stessa cosa :
à
Supponiamo falso l’enunciato di Kelvin - Planck e dimostriamo che il secondo risulta anch’esso falso :
Se l’enunciato di Kelvin - Planck è falso vuol dire che è possibile costruire una macchina in grado di trasformare calore in lavoro direttamente senza scambi con il serbatoio freddo. Ma allora, fornendo questo lavoro prodotto ad un’altra macchina termica che lavora con i due serbatoi a T1 e a T2 riesco a far passare il calore dal serbatoio più freddo a quello più caldo. Complessivamente non c’è stato scambio di lavoro perché effettivamente il lavoro complessivo è 0 perché il lavoro che produce la prima macchina termica viene assorbito completamente dalla seconda macchina termica. Ma allora sono in contraddizione con l’enunciato di Clausius.
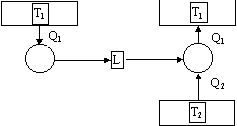
Figura 7
à
Supponiamo ora falso l’enunciato di Clausius e dimostriamo che quello di Kelvin - Planck risulta anch’esso falso :
Se l’enunciato di Clausius è falso vuol dire che è possibile costruire una macchina termica in grado di trasportare calore dal serbatoio più freddo a quello più caldo. Ma allora se colleghiamo un’altra macchina termica che sia in grado di comunicare tra i due serbatoi, potremmo sfruttare il serbatoio caldo per avere lavoro e cedere calore Q2 al serbatoio più freddo.
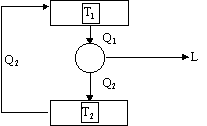
Figura 8
Ma allora complessivamente la quantità di calore Q2 viene fornita dal serbatoio più freddo verso il serbatoio più caldo e poi viene fornita nuovamente al serbatoio freddo stesso. Complessivamente risulta che la macchina termica produce lavoro per il solo effetto dell’arrivo della quantità di calore Q1 dal serbatoio più caldo e questo contraddice l’enunciato di Kelvin - Planck.
Abbiamo così dimostrato che gli enunciati sono tra loro equivalenti.
I due enunciati distinguono quindi questi due casi :
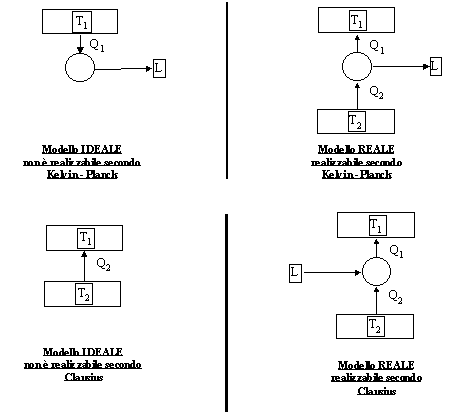
Figura 9
I due enunciati, hanno il problema che a differenza del 1° Principio della Termodinamica non forniscono alcuna informazione che mi può aiutare a capire quale percentuale dell’energia totale è trasformabile.
PROCESSI IRREVERSIBILI E PROCESSI REVERSIBILI
Un processo si dice REVERSIBILE se è possibile riportare sia il sistema sia l’ambiente alla condizione fisica iniziale senza alcun effetto secondario cioè senza aver perso lavoro, calore... Non bisogna confondersi immaginando che un processo è reversibile se solo il sistema ritorna alle condizioni fisiche iniziali senza considerare l’ambiente. Nella realtà è difficile che un processo sia reversibile.
Supponiamo di usare la pompa di una bicicletta lasciando il foro di uscita dell’aria libero. La pressione dell’aria contenuta nel sistema rimane costante perché è libera di uscire, mentre varia il volume di aria contenuto. Se a queste ipotesi aggiungiamo l’ipotesi che non ci sia l’attrito, il sistema termodinamico così considerato effettua un processo reversibile. Se infatti ci muoviamo lungo l’asse del volume nel grafico sotto, notiamo che possiamo comunque sempre ritornare allo stato fisico di partenza senza scambi di calore (ancora ricordando nullo l’attrito).
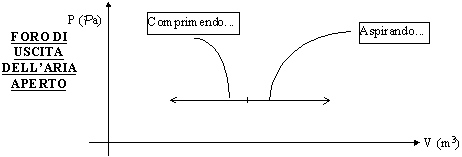
Figura 10 - Pompa della bicicletta con foro aperto
Troviamo un altro processo se invece chiudiamo il foro di uscita dell’aria della pompa. In questo caso, quando comprimiamo, il volume si rimpicciolisce ma aumenta anche la pressione all’interno del sistema che è la nostra pompa. Se ancora è ipotizzabile nullo l’attrito e se il processo viene fatto avvenire lentamente, il processo è come se fosse elastico e quando termino la compressione, vedo che il sistema ritorna nello stato fisico iniziale. Quindi ancora una volta ho avuto un processo reversibile. Graficamente :
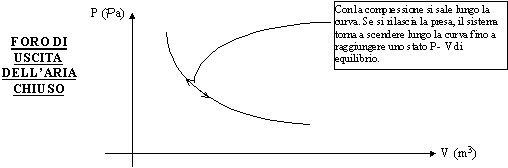
Figura 11 - Pompa della bicicletta con foro chiuso
Se invece ora supponiamo di fare avvenire il processo in maniera molto brusca, nel cammino di andata sul diagramma P - V trovo una curva più ripida di quella di ritorno perché è come se avessi avuto un processo (all’andata) "più adiabatico" cioè con meno scambi di calore. Graficamente :
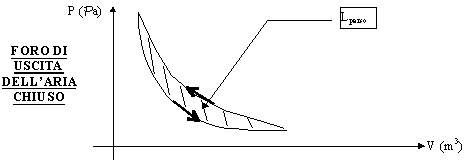
Figura 12 - Pompa della bicicletta con foro chiuso (trasformazione veloce)
Ma allora l’area contenuta tra le due curve (L) rappresenta il lavoro PERSO (quindi energia dissipata). Il lavoro perso è quindi 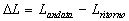 . Questo è un ottimo esempio che spiega perché devono essere sia il sistema che l’ambiente a dover ritornare alle condizioni fisiche iniziali. Infatti se guardiamo questo processo, il sistema torna allo stato iniziale, mentre l’ambiente no perché ha subito l’energia che è stata persa.
. Questo è un ottimo esempio che spiega perché devono essere sia il sistema che l’ambiente a dover ritornare alle condizioni fisiche iniziali. Infatti se guardiamo questo processo, il sistema torna allo stato iniziale, mentre l’ambiente no perché ha subito l’energia che è stata persa.
I processi IRREVERSIBILI sono tutti quei processi che non sono Reversibili. L’irreversibilità può essere :
- INTERNA AL SISTEMA : se dovuta ad esempio ad attrito, alle forze dissipative... che trasformano l’energia meccanica in calore
- ESTERNA : dovuta ai flussi di calore che fluiscono tra i corpi a contatto con il sistema
Un tipico caso di Irreversibilità ESTERNA si ha quando prendiamo la classica pompa della bicicletta ed effettuiamo una compressione. Se dopo la compressione ci fermiamo un attimo, il sistema si raffredda cedendo calore all’ambiente. Se poi rilasciamo, il sistema procede alla decompressione dell’aria in esso contenuta descrivendo una curva più bassa perché il processo inverso (di decompressione) parte da una temperatura più bassa. Graficamente ciò è molto chiaro :
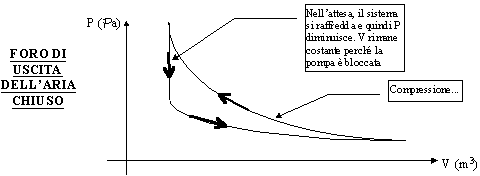
Figura 13
Per eliminare le Irreversibilità esterne bisognerebbe fare in modo che i processi avvenissero in maniera molto lenta e che il sistema fosse a contatto con serbatoi a temperature prossime a quelle del sistema in grado di mantenerne costante la temperatura. Questo però è alquanto infattibile nella realtà.
Le Irreversibilità esterne sono sempre presenti nella realtà, pertanto i processi reversibili non sono possibili.
Le Irreversibilità interne sono invece limitabili a seconda dell’accuratezza con la quale si costruisce il sistema. Se facciamo in modo di isolare termicamente il sistema dall’esterno e se riusciamo ad "eliminare" l’attrito, il processo si può anche considerare INTERNAMENTE INVERTIBILE e cioè il processo non ha irreversibilità interne ma le uniche che creano problemi restano quelle esterne che sappiamo essere ineliminabili nella realtà. Quindi questo potrebbe essere il caso migliore che ci può capitare. In casi del genere siamo sicuri di poter avere il grafico che rappresenta il processo, sul diagramma P - V, perché si tratta di trasformazioni Quasi Statiche. Se invece le trasformazioni considerate non fossero quasi statiche, non sarebbe possibile disegnare il grafico del processo, quindi non potrei immaginare che si tratti di un processo internamente invertibile.
Per focalizzare bene il problema ecco un esempio per capire quando abbiamo una trasformazione reversibile e quando no :
Consideriamo un cilindro contenente un pistone che viene fatto muovere in due differenti modi : a) appoggiando sulla sua "testa" un peso ; b) appoggiando sulla sua "testa" dei granelli di sabbia e aumentandone la quantità pian piano.
Entrambe servono per portare il sistema da uno stato fisico A ad uno stato fisico B :
a)
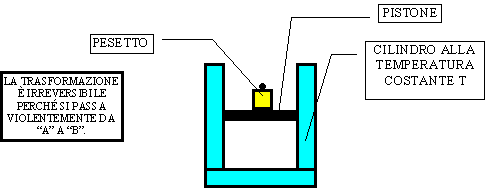
Figura 14 - Processo irreversibile
Graficamente :

Figura 15 - "Diagramma P-V" della trasformazione irreversibile del sistema di Fig. 14
b)
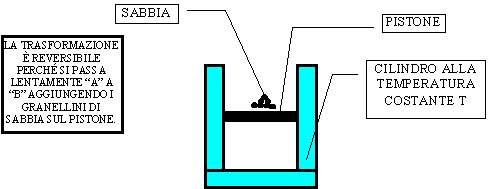
Figura 16 - Processo reversibile
Graficamente :
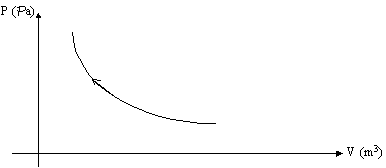
Figura 17 - Diagramma P-V del processo reversibile di Fig. 16
DISUGUAGLIANZA DI CLAUSIUS
Secondo Clausius, data una qualsiasi trasformazione che fa mutare lo stato fisico di un sistema da un punto A ad un punto B del grafico P - V, questa si può sempre approssimare con un cammino composto da 2 curve adiabatiche (curve che descrivono i processi senza scambi di calore con l’esterno) e 1 isotermica (curva che descrive un processo a temperatura costante). Essendo possibile rappresentare graficamente il processo, appare evidente che si tratti di una trasformazione quasi statica e quindi di un processo internamente reversibile.
A seconda della posizione sul diagramma dove si sceglie mettere la curva isoterma, ho infiniti cammini che possono approssimare il percorso originale. Bisogna quindi cercare quella tale per cui l’area sottesa dal cammino approssimante corrisponde all’area sottesa dal cammino realmente percorso. Questo con lo scopo di minimizzare l’errore che si compie nel fare l’approssimazione.
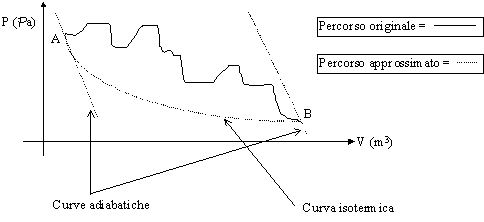
Figura 18 - Trasformazione approssimata con il metodo di Clausius
Con questo procedimento di approssimazione :
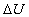 (variazione di energia interna al sistema) rimane la stessa nei due percorsi (reale e approssimato)
(variazione di energia interna al sistema) rimane la stessa nei due percorsi (reale e approssimato)- L (lavoro scambiato) rimane lo stesso perché si è scelta la curva isotermica in maniera che i due percorsi sottendano la stessa area
Quindi scopriamo, dal 1° Principio della Termodinamica, che inevitabilmente anche la quantità di calore scambiata Q tra il sistema e l’ambiente deve essere la stessa :
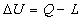
Un procedimento di approssimazione di questo tipo si può applicare a qualsiasi trasformazione quasi statica (quindi internamente reversibile) e anche ad una trasformazione ciclica. In questo caso il ciclo approssimante è composto da tanti piccoli percorsi composti da 2 curve adiabatiche e da 1 curva isoterma, esattamente come nel caso meno complesso di un percorso lineare :
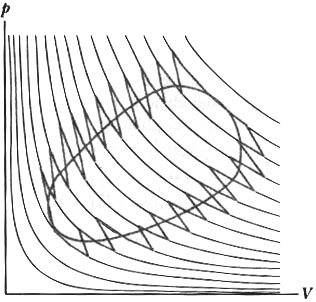
Figura 19 - Processo ciclico approssimato mediante il metodo di Clausius
Quando il sistema sta scambiando calore lungo la curva isoterma, si può immaginare che il sistema stia scambiando calore con un serbatoio che ha la stessa temperatura che ha il sistema lungo questo percorso (si ricorda che l’isoterma è una curva che descrive un processo a temperatura costante).
Analogamente se considero il processo ciclico, devo immaginare che il sistema stia scambiando calore con tanti serbatoi posti tutti alla temperatura evidenziata dalla curva isotermica corrispondente.
Ora proviamo a calcolare l’integrale su un ciclo della quantità 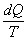 e cioè calcoliamo
e cioè calcoliamo 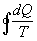 (il cerchietto sul simbolo dell’integrale sta proprio ad indicare che l’integrale va calcolato su un percorso ciclico).
(il cerchietto sul simbolo dell’integrale sta proprio ad indicare che l’integrale va calcolato su un percorso ciclico).
La Disuguaglianza di Clausius dice che :
- se il sistema ha lavorato, nel ciclo, in maniera reversibile allora
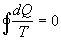
- se il sistema ha avuto irreversibilità esterne allora
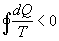
In generale si può dire che 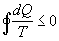 .
.
Se fosse invece 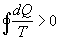 violerebbe il 2° Principio della Termodinamica e cioè in particolare violerebbe l’enunciato di Clausius perché sarebbe possibile costruire una serie di macchine termiche, che lavorano reversibilmente, che complessivamente riescono a spostare calore da un serbatoio freddo ad uno caldo.
violerebbe il 2° Principio della Termodinamica e cioè in particolare violerebbe l’enunciato di Clausius perché sarebbe possibile costruire una serie di macchine termiche, che lavorano reversibilmente, che complessivamente riescono a spostare calore da un serbatoio freddo ad uno caldo.
In effetti però la Disuguaglianza di Clausius esprime il 2° Principio della Termodinamica in una forma algebrica che è difficile da calcolare. Questa disuguaglianza permette di definire una nuova grandezza termodinamica che è l’ENTROPIA.
ENTROPIA
L’Entropia è una FUNZIONE DI STATO e cioè è una funzione il cui valore è indipendente dal cammino scelto per calcolarla ma dipende soltanto dai suoi estremi.
Esattamente come l’Energia interna, l’Entropia ha senso se viene considerato uno stato fisico di riferimento al quale possiamo assegnare un valore di Entropia pari a 0. Tutti i valori di Entropia calcolati in seguito dovranno quindi essere riferiti a questo stato di riferimento.
Per definizione si scrive che :
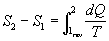
Ma l’integrale a secondo membro può essere calcolato soltanto lungo un cammino che descrive una trasformazione reversibile. Non ha senso calcolarlo se la trasformazione è irreversibile. Questo anche se l’Entropia è una funzione di stato.
Infatti, proprio perché è una funzione di stato, per qualsiasi cammino si ritrova lo stesso valore di 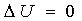 . Ma scegliendo come cammino un percorso irreversibile, il calcolo da fare per capire quanto vale S2-S1 è troppo complicato. Il segreto sta allora nel cercare di scegliere il cammino più adatto, e ciò necessita di un po’ di pratica nella risoluzione dei problemi.
. Ma scegliendo come cammino un percorso irreversibile, il calcolo da fare per capire quanto vale S2-S1 è troppo complicato. Il segreto sta allora nel cercare di scegliere il cammino più adatto, e ciò necessita di un po’ di pratica nella risoluzione dei problemi.
Se si considera il ciclo :
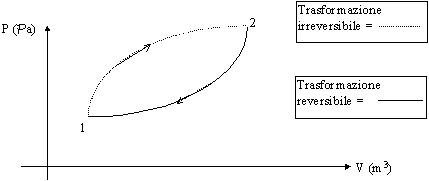
Figura 20 - Differenza tra processi reversibili e irreversibili (non rappresentabili graficamente)
Lungo la trasformazione reversibile si può calcolare :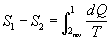
Lungo tutto il percorso si può scrivere :
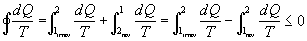 per Clausius
per Clausius
ma allora si trova che :
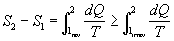
(ammesso che il secondo membro si possa calcolare tenendone presente la difficoltà).
Ma ciò è assurdo perché si trova una contraddizione al fatto che l’Entropia è una funzione di stato. Si dice allora che c’è stata una produzione di Entropia a causa del processo irreversibile (anche se questa enunciazione non è del tutto adatta).
Si trova quindi che :
- un processo REVERSIBILE MANTIENE L’ENTROPIA
- un processo IRREVERSIBILE PRODUCE ENTROPIA
L’Entropia che manca è data da :
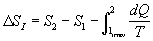
Ma allora si può concludere che :
- se il processo è avvenuto con tutte trasformazioni reversibili, la variazione dell’Entropia del sistema + la variazione dell’Entropia dell’ambiente è uguale a zero.
- se il processo è avvenuto con qualche trasformazione irreversibile, la variazione complessiva di Entropia del sistema + quella dell’ambiente è maggiore di 0.
Questa importante conclusione porta ad enunciare il PRINCIPIO DI NON DIMINUZIONE DELL’ENTROPIA DELL’UNIVERSO.
PRINCIPIO DI NON DIMINUZIONE DELL’ENTROPIA DELL’UNIVERSO
Il principio afferma che complessivamente, l’Entropia dell’universo (che è uguale a sistema + ambiente) può soltanto aumentare. In particolare, dato che nella realtà non è possibile (come si è visto precedentemente) avere processi reversibili, l’Entropia finale non può essere uguale a quella iniziale. Al massimo, in particolari condizioni può aumentare di poco, ma sostanzialmente aumenta sempre.
Si può osservare però che, separatamente, l’Entropia del sistema può anche diminuire, ma in questo caso vorrebbe dire che l’Entropia dell’ambiente alla fine della trasformazione è aumentata di una quantità tale da rendere comunque la variazione di entropia complessiva dell’universo maggiore di 0.
Questa importante conclusione porta, filosoficamente parlando, al concetto secondo il quale non è possibile tornare indietro nel tempo.
![]()



















