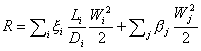Le perdite di carico

Stefano Ghidoni – matricola 125948 – lezione del 31/10/2000 ore 14:30 – 16:30

Verranno trattati i seguenti argomenti:

· Perdite di carico distribuite e concentrate;

· Un’applicazione dell’equazione di Navier: l’equazione di Bernoulli.

Un fluido che scorre dentro una tubazione è soggetto alle cosiddette perdite di carico, ovvero ad un calo di pressione dovuto agli attriti interni dello stesso: il nostro scopo è riuscire a calcolarle, anche se in maniera approssimata. È importante osservare che le leggi che regolano il moto di un fluido non sono, purtroppo, universalmente valide: il modo stesso con cui questo si muove varia in funzione della sua velocità, della viscosità e della densità che lo caratterizzano, e del diametro del tubo entro cui esso fluisce. Per questo si è soliti ricorrere a due modelli per descrivere un fluido in moto: il regime laminare e quello turbolento; il primo prevede che questo sia suddivisibile in tante lamelle che scorrono (non senza attrito) una sull’altra e parallelamente al tubo; il secondo, invece, si basa sull’idea che le varie molecole si muovano in modo caotico, formando vortici. Si sceglie un modello o l’altro a seconda del valore di un parametro, il numero di Reynolds, definito da:

dove D è il diametro del tubo, W la velocità media del fluido, ρ la sua densità e μ la sua viscosità. A seconda del valore di tale parametro, dunque, si usa un modello, piuttosto che l’altro, sapendo che siamo in:

Ø Regime laminare se Re<2.100

Ø Regime turbolento se Re>4.000

Evidentemente, esiste un range entro il quale non vale nessuno dei due modelli: questo viene chiamato zona di transizione.

Possiamo ora prendere in esame le perdite di carico, osservando che vengono a loro volta suddivise in due categorie: quelle distribuite e quelle concentrate. Le prime sono dovute agli attriti che inevitabilmente si generano a causa dello scorrere del fluido nel tubo, perciò sono presenti (distribuite) ovunque nelle tubazioni; le perdite concentrate, al contrario, sono localizzate in un ben preciso punto del percorso, e sono dovute ad ostacoli quali un rubinetto, una diramazione, un restringimento o un allargamento del condotto, un gomito ecc.

Ora che abbiamo definito ciò che vogliamo trattare, possiamo fare un primo calcolo di perdita di carico: per esempio, quella distribuita dovuta ad un tubo rettilineo di sezione circolare di raggio R, e lunghezza L, perfettamente liscio, entro

cui scorre un fluido di viscosità μ in regime laminare: è già stata calcolata

l’espressione della velocità in funzione della caduta di pressione tra due sezioni 1 e 2:

Risolvendo tale equazione rispetto alla caduta di pressione, ed esprimendo il raggio in funzione del diametro, si ottiene:

da cui:

(1)

Il termine è chiamato coefficiente d’attrito, e tale espressione vale solamente sotto le ipotesi che abbiamo fatto, in particolare quelle di tubo liscio, sezione circolare e moto laminare. È anche da notare come l’espressione appena ricavata per la perdita di pressione sia direttamente proporzionale al termine , quindi alla lunghezza relativa del tubo: questo fattore esprime il concetto dei perdita distribuita.

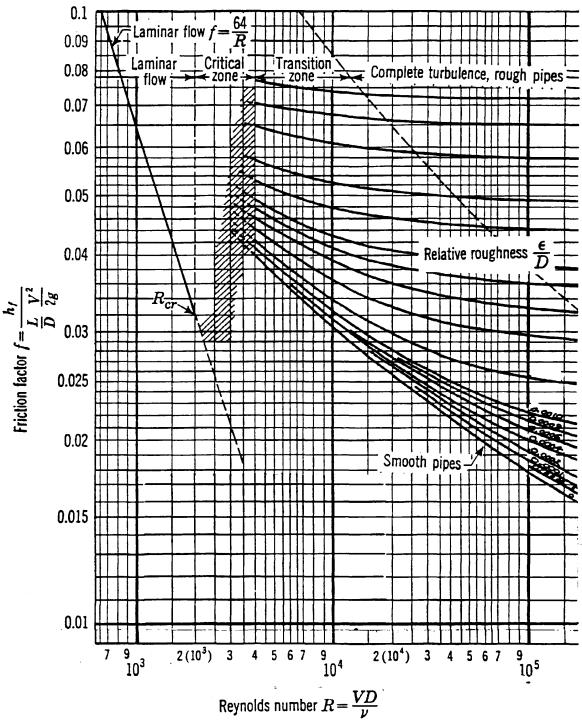
Qualora non valessero le ipotesi sotto le quali abbiamo sviluppato il calcolo, possiamo comunque utilizzare la formula (1) ricavando il coefficiente d’attrito non più per via analitica, ma mediante l’uso di tabelle o del diagramma di Moody, di origine sperimentale, in funzione del numero di Reynolds e della rugosità relativa:

dove D è sempre il diametro del tubo, mentre ε è il valore medio della sua scabrezza (solitamente, entrambi sono espressi in mm).

Osserviamo dunque il diagramma di Moody, che si presenta sotto forma di retta nel caso di regime laminare, in cui vale la relazione:

Aumentando il valore di Re, si entra nel regime turbolento, e il diagramma si divide in più curve, ognuna delle quali rappresenta un particolare valore della scabrezza relativa (relative roughness, nel grafico); la curva inferiore si riferisce al caso del tubo liscio (smooth pipe). Il grafico si usa scegliendo la curva corrispondente alla scabrezza del tubo in esame e individuando su di essa il punto la cui ascissa rappresenta il numero di Reynolds del problema: sull’indice di sinistra si può leggere il valore di ξ. Si noti che la zona critica e quella di transizione non sono trattate: il grafico diventa tratteggiato, e poi subisce una discontinuità; si osservi, infine, che le curve del regime turbolento tendono a spianare all’aumentare del numero di Reynolds.

Abbiamo in precedenza accennato alle perdite di carico concentrate: ci poniamo ora l’obiettivo di trovare una formula per calcolarle, formula che – in linea di massima – non dovrebbe essere troppo diversa da quella già vista per le perdite distribuite; è perciò naturale aspettarsi che il rapporto tra la perdita di pressione e la densità del fluido sia direttamente proporzionale all’energia cinetica del fluido stesso mediante una costante, che è solitamente indicata dalla lettera β; inoltre, dovrà scomparire il termine , che esprimeva il concetto di perdita distribuita. In effetti, la formula usata per calcolare le perdite di carico concentrate è:

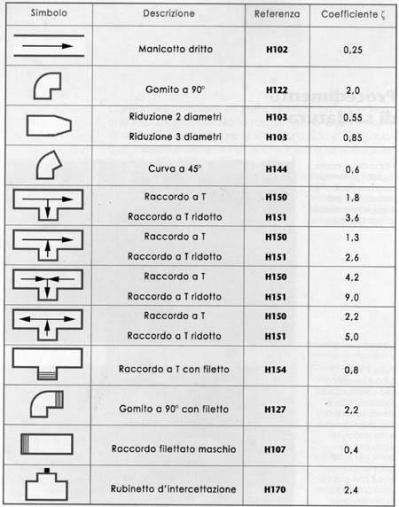
Il termine β, che mantiene il nome di coefficiente d’attrito, dipende dalla particolare geometria dell’oggetto che determina la perdita, ed è tabulato; seguono i valori trovati per alcuni snodi.

In alternativa al metodo appena illustrato, esiste anche uno speciale diagramma costituito da tre linee parallele: sulla prima sono indicati alcuni indici, ognuno dei quali rappresenta un elemento di perdita concentrata; sull’ultima è invece presente una scala di lunghezze che indica il diametro interno del tubo: congiungendo con un segmento i due punti che individuano il problema, questo intercetta sulla linea centrale un particolare valore espresso in metri, che prende il nome di lunghezza equivalente: si tratta della lunghezza che un tubo deve avere per generare la stessa perdita di carico dovuta all’elemento che stiamo analizzando. Perciò è possibile trovare le lunghezze equivalenti di tutti gli elementi che generano perdite di carico localizzate, e calcolare la perdita totale considerando solo quelle distribuite dovute ad un percorso allungato ad hoc.

Come si può vedere dalla tabella, anche un restringimento della tubazione è fonte di perdita di carico, e lo stesso vale per un allargamento; il coefficiente da usare dipende in questo caso sia dalla variazione di diametro, sia da quanto bruscamente questa avviene. Se cambia il diametro, anche la velocità del fluido si adegua, e, più precisamente, aumenta se il diametro si restringe, e viceversa. Ciò deriva dal considerare che la portata in massa delle tubazioni deve rimanere costante in ogni punto, quindi anche nelle sezioni 1 e 2 in figura:

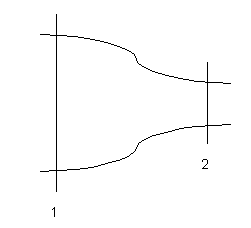
Possiamo esprimere tali portate nel solito modo:

Se il fluido che trattiamo è un liquido, si può considerare costante la densità che, quindi, si semplifica:

quindi, se diminuisce la sezione, aumenta la velocità.

Fino ad ora abbiamo affrontato il calcolo delle perdite di carico dapprima in un caso semplice (tubo liscio, sezione circolare, moto laminare), poi abbiamo via via rimosso le semplificazioni per portare la nostra trattazione ad un caso sempre più generale: in quest’ottica, l’ultimo passo che ci manca è quello di considerare la sezione non più circolare, ma di forma qualsiasi. Infatti, è a volte utile o necessario utilizzare tubi di sezione particolare, come quella quadrata, quella triangolare ecc., nel qual caso la teoria finora sviluppata non funziona in maniera efficiente; è però possibile modificare un parametro per sfruttarla di nuovo. Allo scopo, introduciamo il concetto di diametro equivalente: con questo, è possibile trattare i tubi di qualsiasi sezione come se questa fosse circolare, ed utilizzare quindi tutte le formule viste finora; esso è definito come il rapporto tra il quadruplo dell’area della sezione e il perimetro bagnato, ovvero quello “visto” dal fluido:

Evidentemente, per tubi di sezione circolare il diametro reale e quello equivalente coincidono; proviamo poi a fare il calcolo in casi semplici:

ü Sezione quadrata:

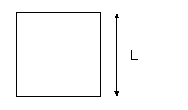
Detto L il lato del quadrato, il diametro equivalente è dato da:

ü Sezione triangolare:

Considereremo il caso più semplice: triangolo equilatero:

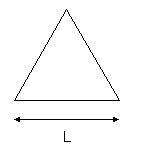
ü Sezione ad anello:

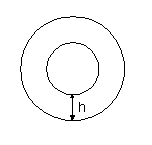
In questo caso è segnato sul disegno solamente il passo h tra il tubo interno e quello esterno, poiché è l’unico parametro in funzione del quale si esprime il diametro equivalente; infatti, se R e r sono, rispettivamente, il diametro del tubo esterno e quello del tubo interno, si può scrivere:

Una volta spiegato come calcolare le perdite cui un fluido va incontro scorrendo nei tubi ed attraversando gli ostacoli che eventualmente incontra, è ora facile fare l’analisi di un sistema nel suo complesso, dato che questo è scomponibile negli elementi semplici che sappiamo gestire: dovendo, quindi, scegliere una pompa per mantenere un certo flusso dentro un sistema, questa deve generare una differenza di pressione superiore alla perdita di carico totale, data da:

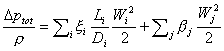
Proviamo a mettere in pratica quello che è stato illustrato.

Problema.

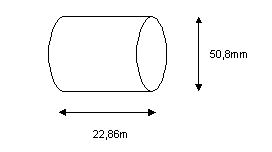
Si calcoli la perdita di carico dovuta ad un tubo di diametro D=50,8mm e lunghezza L=22,86m, con una rugosità media m, se vi scorre ammoniaca alla temperatura di –12,2°C alla velocità di .

Risoluzione.

L’ammoniaca ha viscosità e densità .

Una volta scoperti questi dati dalle tabelle, è possibile risolvere il problema. La prima cosa da fare è scoprire se siamo in regime laminare o turbolento, visto che il procedimento risolutivo, come già osservato, dipende fortemente da questa constatazione; calcoliamo dunque il numero di Reynolds:

Il regime è dunque fortemente turbolento.

Calcoliamo poi la scabrosità relativa:

Avendo ora Re e la scabrosità, è possibile, grazie al diagramma di Moody, determinare il coefficiente d’attrito: risulta . Il passo finale è, ovviamente, il calcolo della perdita di carico distribuita:

Dall’equazione di Navier a quella di Bernoulli.

Lo studio della fluidodinamica si basa su un’equazione che ne costituisce la base: l’equazione di Navier, già enunciata in altri contesti, e che qui ricordiamo:

Quest’equazione rappresenta l’andamento della derivata sostanziale della velocità in funzione della forza di gravità (primo termine), e di quella dovuta alle pressioni (secondo termine), le quali costituiscono il “motore” del fluido, ovvero le cause che tendono a muoverlo; poi, viene contemplato l’ultimo termine, che rappresenta gli impedimenti che ostacolano il moto del fluido stesso. Grazie ad essa è possibile, analizzando le condizioni al contorno del fluido, dedurre il vettore velocità in funzione delle tre coordinate spaziali e di quella temporale: . Purtroppo, anche se questa equazione ha validità generale, e – almeno in linea teorica – potrebbe risolvere in maniera accurata i problemi della fluidodinamica, la sua espressione è evidentemente molto complessa, quindi non viene di fatto usata nei calcoli per le situazioni reali. È però possibile ricavare da questa espressione la ben nota (e usata) equazione di Bernoulli, che è già stata utilizzata in altri ambiti per la risoluzione pratica di alcuni problemi. Prendiamo quindi in considerazione un tubo di flusso: esso è un tubo ideale che non può essere attraversato dal fluido se non dalle sezioni di ingrasso e di uscita; in altre parole, la sua superficie laterale è “impermeabile”. Di primo acchito potrebbe sembrare un concetto strano, ma basta pensarlo come il tubo generato da tutte le linee di flusso che passano per una curva chiusa, che determina così una delle due sezioni; l’altra è individuata da un’ulteriore linea chiusa che intercetta le medesime linee di flusso. Risulta ora più naturale pensare che la superficie laterale del nostro tubo ideale sia impermeabile: le linee di flusso non si incrociano mai; naturalmente, nulla garantisce che le due sezioni siano uguali, e infatti generalmente non lo sono. Infine, osserviamo che non è possibile sfruttare l’ipotesi dell’aderenza, poiché le pareti di un tubo di flusso non esistono.

Ipotizziamo che il nostro sistema si trovi in regime stazionario: ciò porta a considerare nulle tutte le derivate temporali, e a porre uguali il flusso entrante e quello uscente; integriamo poi l’equazione di Navier, facendo in tal modo un bilancio dell’energia. Il calcolo è assai complesso, e viene perciò omesso; il risultato è:

dove i coefficienti e , che tengono conto dei profili di velocità, vengono generalmente posti uguali a 1, considerando la velocità stessa uniforme sulle sezioni; si noti inoltre come siano stati considerati volume e lavoro specifici. Il termine prende il nome di energia meccanica specifica, ed esprime una sorta di resistenza idraulica: quella che oppone il fluido allo scorrimento, a causa della propria viscosità, ed è a volte indicata con la lettera R; z₁ e z₂ sono invece le quote delle due sezioni: non è detto che il tubo sia orizzontale. Tentiamo ora di sviluppare ulteriormente, assumendo unitarie le costanti di cui abbiamo parlato; per prima cosa cerchiamo dunque di eliminare i due integrali, che tendono a far aumentare la complessità dei calcoli, osservando che, per definizione:

avendo indicato con q_sist.
chiuso la somma del calore del fluido e di quello dovuto ai fenomeni dissipativi. Ricordando che il volume specifico è l’inverso della densità:

possiamo eliminare l’integrale che era rimasto:

Riusciamo dunque a scrivere l’equazione di Bernoulli, priva di integrali:

Mettiamo in luce, da ultimo, che il termine R non è altro che l’insieme delle perdite di carico che abbiamo formalizzato all’inizio della trattazione, il che è naturale, visto che deve esprimere la resistenza che il fluido oppone allo scorrimento. Perciò è possibile esplicitare R come segue: