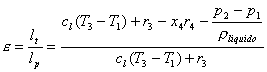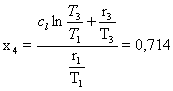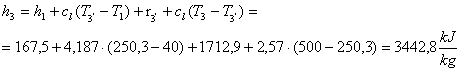MACCHINA DI
RANKINE
Il problema
di realizzare un ciclo termodinamico che produca la massima quantità di lavoro
a parità di calore entrante, ha come soluzione ottimale la macchina di Carnot. Si
tratta però di una macchina ideale, perché opera su un ciclo reversibile.
Nella
pratica, la soluzione che in maniera più brillante approssima quella ottimale è
la macchina di Rankine, questa applicazione, dal punto di vista ingegnerìstico, è la più importante
della termodinamica e consiste nello studio e nel perfezionamento d’apparati
per la conversione continua, anche se non completa, di calore in lavoro.
In queste macchine, atte a
trasformare calore in lavoro meccanico, si utilizza come fluido intermediario
l’acqua che viene alternativamente vaporizzata e condensata: si parla in tal
caso di macchine a vapore però l’ acqua usata da questo tipo di cicli deve
essere filtratata e a Ph controllato perciò assai costosa.
Il ciclo termodinamico sul
quale è basato il funzionamento delle macchine a vapore, è il Ciclo Rankine (un esempio di tali
macchine sono quelle usate nelle centrali termoelettriche e nucleari).
Una macchina di Rankine è tipicamente composta di quattro elementi (Fig.
1): una pompa, una caldaia, una turbina e un condensatore tutti questi
componenti sono dei sistemi aperti,
insieme i quattro componenti costituiscono un sistema chiuso
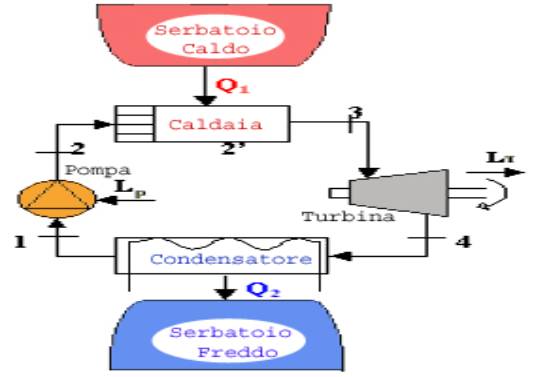
Fig. 1
1®2: il fluido, che è
nella fase liquida, subisce una compressione isoentropica (s è costante); ciò viene realizzato mediante una pompa, sistema
aperto che non scambia calore:
(lavoro speso per portare acqua in caldaia)
2®2’, 2’®3: In caldaia l’acqua viene
dapprima riscaldata fino alla temperatura di vaporizzazione, quindi vaporizzata
a temperatura costante fino allo stato di vapore saturo secco (titolo
unitario).
La caldaia utilizzata è un
sistema aperto che non scambia lavoro.
3®4: il fluido, che ora
è nella fase di vapore saturo secco, passa attraverso a una turbina, sistema
aperto che non scambia calore, e, espandendosi in modo isoentropico (si rimane sotto la curva limite superiore), compie
lavoro.
Per studiare il
funzionamento di questo tipo si può ricorrere a 3 tipi di diagramma :
: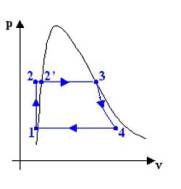
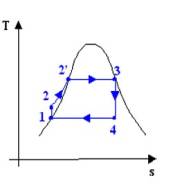
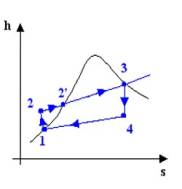
Fig. 2
I più usati
sono naturalmente il diagramma pv ed
il diagramma ts (il diagramma hs o diagramma di Mollier è di uso specialistico);
però mentre sappiamo che il diagramma pv è utile perché le aree sottese rappresentano il lavoro
svolto dal ciclo (fig .3 )
vediamo ch ts le aree sono date da:
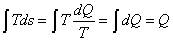
cioè l’area rappresenta un calore
e non più un lavoro, ed in particolare si ha che :
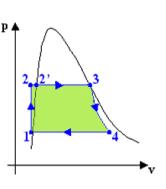
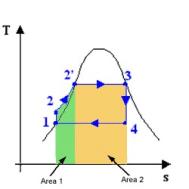
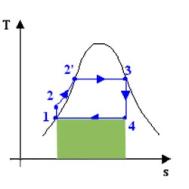
Fig. 3 Fig. 4 Fig. 5
dove in fig. 4 l’Area 2
rappresenta il calore latente di
vaporizzazione mentre l’ Area 1 sommata
all’ Area 1 danno il calore entrato
nel ciclo (q23).
In fig. 5 l’area evidenziata
rappresenta il calore uscito dal ciclo (q41)
per cui il l’ area del ciclo (che è data da q23 - q41 = l) corrisponde al lavoro
effettuato come differenza tra calore assorbito e calore rilasciato dal ciclo.
Da questo si
evince come sia molto comodo il
diagramma ts per vedere il
coefficiente economico, infatti essendo :
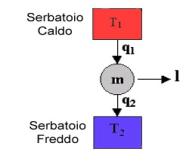
Fig. 6
dove q1=q23 mentre q2=q41 per cui l’ area del ciclo è uguale a l=q23-q41 da cui ricordando che
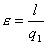 si evince come
sia molto comodo il diagramma ts che ci dà :
si evince come
sia molto comodo il diagramma ts che ci dà : 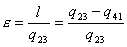
A questo punto vediamo cosa succede
dal punto di vista energetico nei 4 elementi che compongono il ciclo (nelle
equazioni di bilancio energetico trascureremo lc ed lp).
1 : (Pompa) 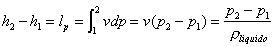
2: (Caldaia) 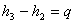 da cui
da cui 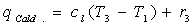
3: (Turbina) 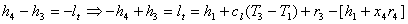
(Qua insorge un problema perché x4 non è dato e per
questo deve essere stimato)
4: (Condensatore) 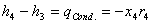
Per cui infine 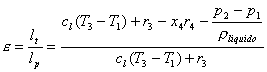
Confrontiamo il ciclo di Rankine e il ciclo di
Carnot (che è il ciclo con il migliore coefficiente termodinamico ,inoltre
perchè questo abbias enso i 2 cicli devono operare tra le stesse temperature
estreme):
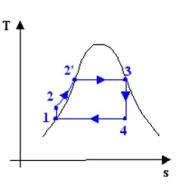
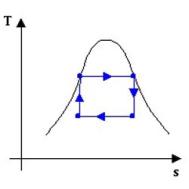
Fig. 7
il ciclo di Rankine presenta
delle irreversibilità; ad esempio, il fatto che man mano che si prende calore
dai fumi di combustione la loro temperatura diminuisca, è una causa di
irreversibilità esterna; il fluido è comunque sempre in equilibrio
termodinamico, per cui l’area del ciclo nel diagramma rappresenta la differenza
tra il calore assorbito e il calore ceduto, cioè il lavoro prodotto, come per
il ciclo di Carnot.
Guardando le figure, è lecito
aspettarsi che il rendimento termodinamico 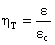

(rapporto tra il coefficiente
economico della macchina di Rankine e quello della macchina di Carnot) assuma
un valore vicino all’unità.
Esempio
Numerico
Determinare il coefficiente
economico e per un ciclo di Rankine con
T1 = 40
°C
P1=7.38 kPa
T2 = 250,3 °C P2=4000 kPa
Dalle considerazioni
precedenti si ha che :
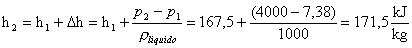
Dopodichè :
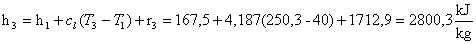
Mentre:
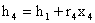 dove
dove
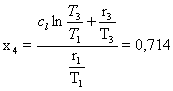
Per cui: 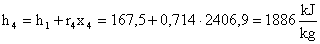
Cioè : 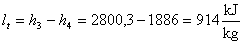
Da cui otteniamo :
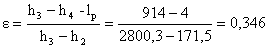
Che non sembra particolarmente
alto per cui confrontiamolo con il ciclo di Carnot:
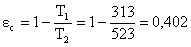
Quindi: 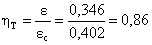 che sembra
abbastanza buono.
che sembra
abbastanza buono.
MACCHINA DI RANKINE CON SURRISCALDATORE
Abbiamo visto
che il vapore saturo secco in uscita dalla caldaia viene fatto espandere
utilizzando una turbina; ma poiché nello stato 4 il titolo è molto minore di 1, ci sono gocce di liquido che
entrano in violento contatto con le parti meccaniche della turbina e le erodono.
In genere si
adotta la seguente soluzione:
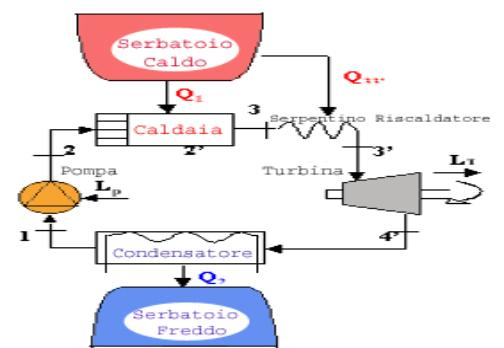
Fig. 8
Il serpentino
riscaldatore fa sì che il fluido in uscita dalla caldaia passi dalla fase di
vapore saturo secco in quella di vapore
surriscaldato.
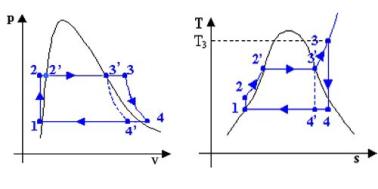
Fig. 9
E’ evidente che il
valore del titolo nello stato 4’ è
molto più vicino a 1.
Inoltre evidentemente ora abbiamo
h3 e x4 che sono maggiori percil vediamo subito un :
Esempio Numerico
Determinare
il cefficiente economico per un ciclo di Rankine con surriscaldatore, date:
T1 = 40 °C
T3’ = 250,3 °C
T3 = 500 °C
Troviamo che :
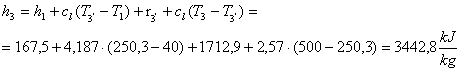
Essendo: 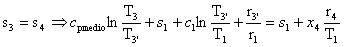
Da cui : 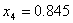
Essendo :
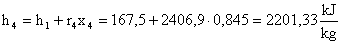
Troviamo:
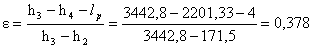
NOTA:
Per confrontare
la macchina di Rankine con surriscaldatore e la macchina di Carnot, è sbagliato
calcolare ht come
rapporto tra i coefficienti economici
con
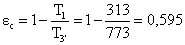
Si otterrebbe 0,635: cioè peggio
rispetto al caso della macchina di Rankine senza surriscaldatore?
Bisogna
guardare il diagramma che descrive l’andamento della temperatura del serbatoio
caldo (fumi prodotti bruciando combustibile e aria) in funzione della quantità
di calore da esso sottratta, e confrontare le due macchine in base alla
quantità di calore che effettivamente riescono a sfruttare (exergia):
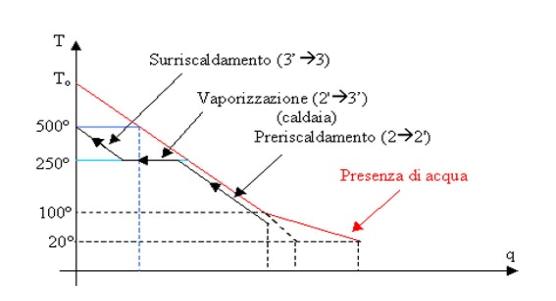
In rosso: diagramma T-q del serbatoio caldo, in
nero: trasformazione 2®3 nel ciclo di Rankine con
surriscaldamento, in blu e celeste: due esempi di passaggi analoghi nel ciclo
di Carnot
Fig. 10
Concludendo, solo con un’infinita successione di cicli di Carnot si
riesce ad estrarre tutto il calore dai fumi:
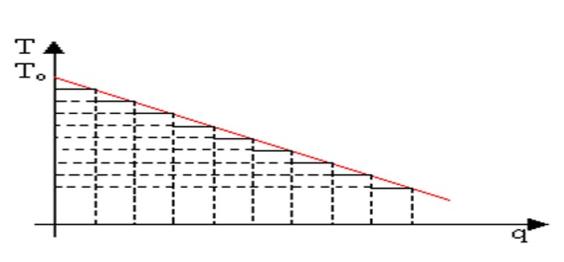
Estrazione totale del calore per mezzo di infiniti cicli di
carnot
Fig. 11
La macchina
di carnot sarebbe ottima se il serbatoio caldo fosse a temperatura costante.
Tabelle
|
(°C)
|
p
(BAR)
|
hl
(kJ/kg)
|
r
(kJ/kg)
|
sl
(kJ/kgK)
|
|
0,01
|
0,006112
|
0
|
2501,6
|
0
|
|
4
|
0,008129
|
16,8
|
2492,1
|
0,0611
|
|
8
|
0,010720
|
33,6
|
2482,6
|
0,1213
|
|
12
|
0,014014
|
50,4
|
2473,2
|
0,1805
|
|
16
|
0,018168
|
67,1
|
2463,8
|
0,2388
|
|
20
|
0,023366
|
83,9
|
2454,3
|
0,2963
|
|
24
|
0,029821
|
100,6
|
2444,9
|
0,3530
|
|
28
|
0,037782
|
117,3
|
2435,4
|
0,4088
|
|
32
|
0,047534
|
134,0
|
2425,9
|
0,4640
|
|
36
|
0,059400
|
150,7
|
2416,4
|
0,5184
|
|
40
|
0,073750
|
167,5
|
2406,9
|
0,5721
|
|
44
|
0,091001
|
184,2
|
2397,3
|
0,6252
|
|
48
|
0,11162
|
200,9
|
2387,7
|
0,6776
|
|
52
|
0,13613
|
217,6
|
2378,1
|
0,7293
|
|
56
|
0,16511
|
234,4
|
2368,4
|
0,7804
|
|
60
|
0,19920
|
251,1
|
2358,6
|
0,8310
|
|
64
|
0,23912
|
267,8
|
2348,8
|
0,8809
|
|
68
|
0,28563
|
284,6
|
2338,9
|
0,9303
|
|
72
|
0,33958
|
301,4
|
2329,0
|
0,9792
|
|
76
|
0,40191
|
318,1
|
2318,9
|
1,0275
|
|
80
|
0,47360
|
334,9
|
2308,8
|
1,0753
|
|
84
|
0,55573
|
351,7
|
2298,6
|
1,1225
|
|
88
|
0,64948
|
368,5
|
2288,4
|
1,1693
|
|
92
|
0,75608
|
385,4
|
2278,0
|
1,2156
|
|
96
|
0,87686
|
402,2
|
2267,5
|
1,2615
|
|
100
|
1,01325
|
419,1
|
2256,9
|
1,3069
|
|
104
|
1,1668
|
435,9
|
2246,3
|
1,3518
|
|
108
|
1,3390
|
452,9
|
2235,4
|
1,3964
|
|
112
|
1,5316
|
469,8
|
2224,5
|
1,4405
|
|
116
|
1,7465
|
486,7
|
2213,4
|
1,4842
|
|
120
|
1,9854
|
503,7
|
2202,2
|
1,5276
|
TAB.1 – Vapore Saturo
T
(°C)
|
h
(kJ/kg)
|
s
(kJ/kgK)
|
|
250
|
2800,3
|
6,0685
|
|
300
|
2962,0
|
6,3642
|
|
350
|
3095,1
|
6,5870
|
|
400
|
3215,7
|
6,7733
|
|
450
|
3331,2
|
6,9388
|
|
500
|
3445,0
|
7,0909
|
|
550
|
3558,6
|
7,2333
|
|
600
|
3672,8
|
7,3680
|
|
650
|
3787,9
|
7,4961
|
|
700
|
3906,6
|
7,5947
|
TAB.2 – Vapore surriscaldato
(p = 40 BAR, hl
= 1087,4 kJ/kg)
T
(°C)
|
cp
(kJ/kgK)
|
|
300
|
3,136
|
|
350
|
2,891
|
|
400
|
2,742
|
|
450
|
2,648
|
|
500
|
2,579
|
|
550
|
2,533
|
|
600
|
2,500
|
|
650
|
2,475
|
|
700
|
2,458
|