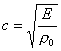Il Suono
La velocità del suono
Andamento
Spaziale
Campo di Frequenza
Pressione Sonora
Legami tra Pressione
e Velocità
L’acustica è una scienza che nasce come tale quando i
sistemi elettronici di gestione del suono non erano ancora nati.
Questa conosce un grande sviluppo a partire dal 1991
infatti è da qui che il suo studio viene coadiuvato da dispositivi elettronici
e da tecniche di elaborazione numerica del segnale il cui sviluppo ne è
addirittura stato fagocitato.
L’acustica è quindi la
scienza che studia il suono.
Oggi tuttavia la gestione
del suono segue uno schema ben definito.
Il suono viene
elettronicamente convertito in segnale elettrico tramite una operazione di
trasduzione questo poi diviene una sequenza numerica; quest’ultimo passaggio da
segnale elettrico a numeri è detto di conversione; è logico pensare che tale
percorso si possa seguire anche in direzione opposta.
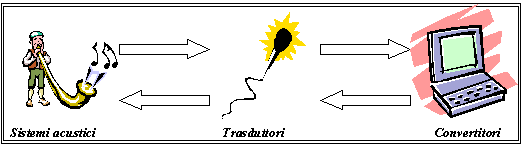
Fig.1 Lo schema illustra la logica con cui si
esegue la progettazione di impianti per la riproduzione sonora.
Il funzionamento di un impianto di diffusione sonora che utilizza microfoni digitali ad
esempio segue precisamente lo schema di
figura uno in entrambe i versi.
Vi è tuttavia la
possibilità di saltare uno di questi stadi.
Esistono cioè apparati
che non utilizzano tutti e tre i blocchi dello schema, i sistemi analogici per
esempio si fermano alla trasduzione del segnale acustico in elettrico, altri,
addirittura, si arrestano quando al primo stadio cioè ai cosiddetti sistemi
acustici che non necessitano di parte elettrica.
Un esempio è costituito dagli
interfoni metallici usati sulle vecchie navi.
Il nostro compito ed
obbiettivo rimane comunque l’apprendimento di tecniche che ci consentano di
effettuare l’analisi sonora e il pieno
controllo del suono.
Suono
Il suono è una forma di
trasporto di energia meccanica che avviene senza trasporto di materia.
Tale trasporto per potersi
compiere necessita di un mezzo.
Il mezzo deve soddisfare due
caratteristiche: deve essere dotato di massa e di elasticità; proprietà che gli
conferiscono il nome di elastico-massivo.
Il suono insomma è una delle tante forme in cui si può presentare l’energia
infatti si usa spesso parlare di energia acustica; l’aspetto energetico è ancora una volta in primo piano.
Oggi si è in grado di misurare il flusso di energia e
dimensionare proprio sulla base di queste misurazioni la potenza (watt) di un
sistema acustico.
Ritorniamo
ora al concetto di mezzo di propagazione.
In
proposito è utile citare l’esperimento della sveglia.
Se si pone una sveglia sotto
una campana di vetro e si aziona la suoneria si osserva che il suono può
propagarsi, ma non appena tramite una pompa da vuoto si toglie l’aria dalla
campana il suono si affievolisce fino a scomparire.

Fig.2 L’esperimento della
sveglia dimostra che una volta spinto il vuoto, cioè privata l’onda acustica
del mezzo, la propagazione acustica diventa nulla.
Questo conferma quanto
detto fino ad ora il suono necessita cioè di un mezzo, l’aria in questo caso, per
potersi propagare.
Il modello fisico di tale
mezzo è una successione di volumi dotati di massa e di molle connesse tra loro,
se io perturbo la quiete di uno di questi volumi questo inizierà ad oscillare
attorno alla sua posizione di equilibrio caricando e scaricando le molle che la
connettono alle masse adiacenti che, a loro volta, iniziano ad oscillare.
Il fenomeno ha un certo
tempo di propagazione che, come vedremo, dipende solo dal mezzo.
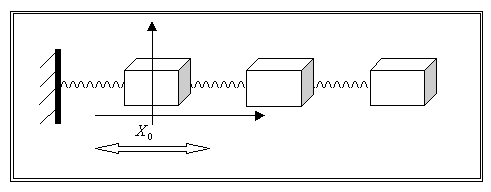
Fig.3 La figura rappresenta in
maniera intuitiva il mezzo elastico massivo di cui necessita l’onda per
propagarsi. Come si è cercato di rappresentare le particelle del mezzo vengono
messe in movimento rispetto ad una posizione iniziale 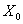 .
.
La velocità del suono
Per intuire l’origine di
un’onda sonora si pensi ad un cilindro pieno di aria, il mezzo, all’interno del
quale scorre uno stantuffo azionato da
un albero mosso a sua volta da un motore che possiede una certa velocità
angolare (w).
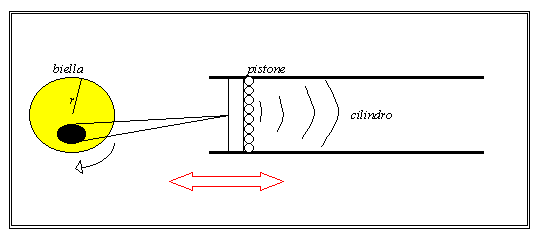
Fig.4 Il disegno rappresenta
schematicamente un generatore di onde acustiche, il pistone infatti perturba lo
stato di quiete delle particelle del mezzo che si mettono ad oscillare intorno
ad una iniziale posizione di equilibrio.
Grazie alla legge dell’aderenza
che ereditiamo dalla fluidodinamica avremo che il primo strato di particelle
aderenti alla superficie del pistone asseconderanno il movimento di questo
seguendolo nelle sue oscillazioni.
Se questo sistema si avvale
di una biella con raggio r e velocità angolare w allora le oscillazioni dello
stantuffo ad essa collegato e quindi delle particelle che vi aderiscono segue
la legge del moto armonico:
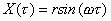 (1)
(1)
Dove X rappresenta la
posizione delle particelle al variare del tempo, r il raggio della biella che muove il pistone
ed w la frequenza.
.
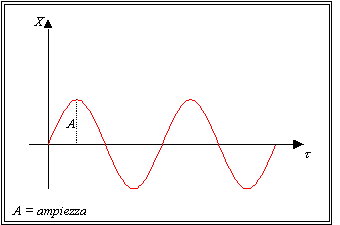
Fig.5 Andamento spaziale delle particelle in funzione del tempo.
La legge del moto appena vista ci impone tuttavia l’introduzione
di due grandezze di cui seguiamo nella definizione.
La prima il periodo, indicato
con la lettera T , che misurato in secondi (s) è il tempo impiegato
dal nostro pistone a compiere un ciclo del suo movimento oscillatorio; sarebbe
il duale del periodo della sinusoide.
La seconda grandezza da introdurre
è la frequenza che definita come l’inverso del periodo, si indica con la
lettera f.
Contrariamente a quanto si
sarebbe tentati di credere non si misura in (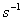 ) ma con una regolare unità di misura, fornita dal sistema
internazionale, l’Hertz (Hz).
) ma con una regolare unità di misura, fornita dal sistema
internazionale, l’Hertz (Hz).
Ora è logico pensare che se
il mio cilindro compie cinquanta oscillazioni al secondo l’onda acustica da
esso prodotta avrà una frequenza di 50 Hz.
Una terza e non meno
importante grandezza da definire è l’ampiezza, A, questa rappresenta
l’escursione spaziale rispetto alla posizione di equilibrio che l’onda acustica
porta ad avere alle particelle del mezzo.
L’ampiezza , che si misura
in metri (m), dipende da quanto è “forte” il suono; è una grandezza
fondamentale nelle operazioni di amplificazione che hanno il solo scopo di
aumentare l’ampiezza del segnale trattato, non variando la frequenza.
Nel caso dell’onda generata
dal pistone questa è pari a r cioè al raggio della biella.
A questo punto possiamo
ritoccare la legge del moto vista precedentemente inserendo l’ampiezza al posto di r:
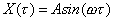 (2)
(2)
Come sappiamo questa legge
indica la posizione dello stantuffo e quindi delle particelle ad esso aderenti
al variare del tempo quindi la sua derivata dovrà indicare la velocità u
con cui queste si muovono intorno alla loro posizione di equilibrio:
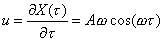 (3)
(3)
come si vede siamo passati da
una funzione seno a una coseno equesto è normale infatti quando l’oscillazione
è massima la velocità è nulla e nell’istante in cui la particella si trova
nella sua posizione di equilibrio la velocità è max.
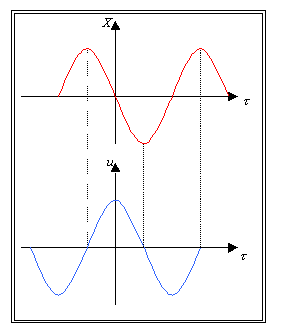
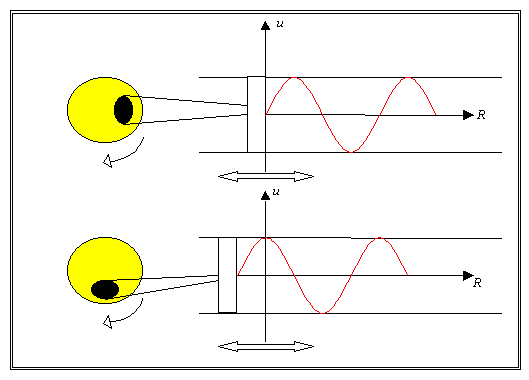
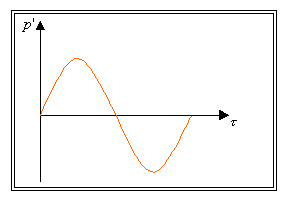
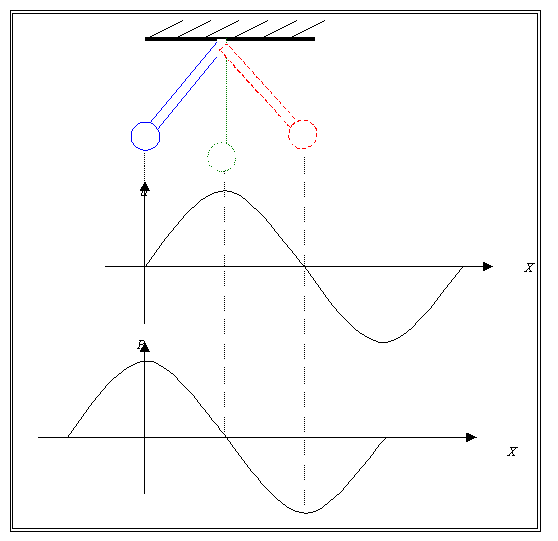
Fig.6 I due grafici
mostrano la caratteristica di velocità
delle particelle ed andamento spaziale di queste in funzione del tempo. Quando
è massima una è nulla l’altra.
Per ottenere
l’accelerazione delle particelle è ovvio dover derivare rispetto al tempo la
velocità quindi l’accelerazione indicata con la lettera (a) è:
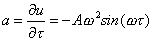 (4)
(4)
La velocità delle particelle
di cui fino ora si è trattato non è da confondersi con quella di propagazione
del suono.
Questa infatti, come già
detto, dipende dal mezzo.
La particella perturbata
dall’onda acustica inizia ad oscillare mettendo in movimento quelle adiacenti,
potremmo dire quindi che la velocità con cui si propaga il suono in un mezzo
corrisponde alla distanza per cui le particelle risultano perturbate diviso il
tempo che tale propagazione di perturbazione ha impiegato a manifestarsi.
L’operazione di derivazione
della legge del moto mette in risalto un altro interessante aspetto di un’onda
acustica.
Infatti le derivate portano
nella velocità e nell’accelerazione delle particelle un termine che è
proporzionale alla frequenza.
Questo fa si che diagrammando
spostamento, velocità e accelerazione in funzione della frequenza
si pervenga ad un risultato del tipo descritto in figura:
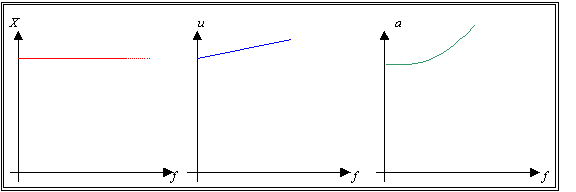
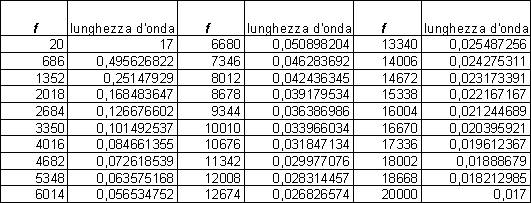
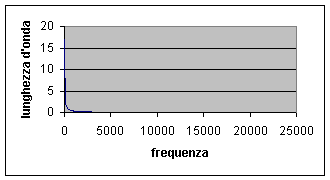
Fig.7 I
grafici mostrano alla luce delle considerazioni analitiche le caratteristiche
rispettivamente di andamento spaziale velocità di oscillazione delle particelle
ed accelerazione delle particelle, al variare della frequenza.
Nella
realtà tuttavia la cose non vanno proprio così infatti più spesso le sorgenti di suono non sono a
spostamento costante ma sono a velocità costante; prendendo un altoparlante ed
applicandogli sempre la stessa tensione e variando la frequenza arriverò ai
risultati riportati in figura:
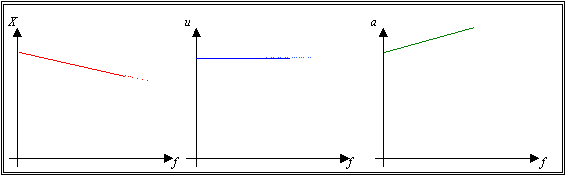
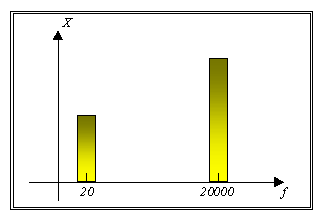
Fig.8 Grafici dell’andamento
spaziale, velocità ed accelerazione delle particelle al variare della frequenza
questa volta alla luce dei dati sperimentali.
Solitamente però la
velocità è molto piccola rispetto alla velocità del suono quest’ultima infatti
è dipendente unicamente dal mezzo
mentre quella delle particelle dipende da quanto segnale portano; si pensi ad
esempio ad un processo di amplificazione che a frequenza costante aumenta
l’ampiezza dell’onda nella stessa unità di tempo allora le particelle dovranno
spazzare una distanza di dimensioni superiori e questo è possibile grazie ad un
aumento di velocità delle particelle.
Andamento spaziale
Per comprendere meglio i
concetti che esprimeremo consideriamo nuovamente il cilindro in cui si muove il
pistone e prendiamo un punto di ascolto al suo interno posto ad una distanza R
dal pistone; è ovvio pensare che la legge del moto delle particelle in tale
punto sia a meno di un ritardo uguale a quella che ho per le particelle che
aderiscono al pistone.
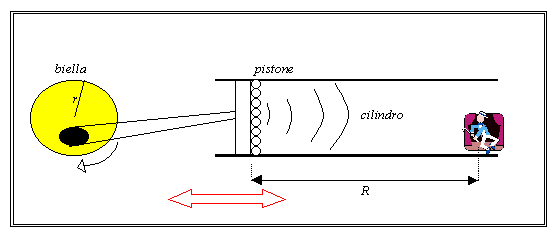
Fig.9 Il disegno mostra la
ovvia e più probabile possibilità di porre un punto di ascolto ad una certa
distanza dalla sorgente acustica; la distanza in questo caso è indicata con la
lettera R.
Tale ritardo è dovuto al
tempo che l’onda acustica impiega a giungere all’orecchio dell’ascoltatore
posto alla distanza R dalla sorgente, quindi in tale punto la legge del moto sarà:
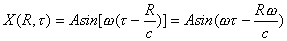 (5)
(5)
dove t è lo spazio che l’onda deve percorrere e c è
la velocità di propagazione del suono.
Il loro rapporto rappresenta
il tempo di ritardo.
Il rapporto (w/c) è una nuova grandezza
detta numero d’onda e le sue dimensioni sono [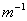 ] è solitamente rappresentata con la lettera k.
] è solitamente rappresentata con la lettera k.
Alla luce di questa nuova
grandezza la legge del moto diviene:
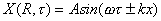 (6)
(6)
In cui il segno della somma,
in parentesi, è dettato dal fatto di considerare il punto di ascolto a
monte o a valle della sorgente.
Rimane ora da mettere in
luce il rapporto tra w ed f; la frequenza
rappresenta infatti il numero di giri che il mio pistone, per esempio, compie
nell’unita di tempo.
w è la pulsazione che invece
rappresenta il numero di radianti al secondo e poiché a fare un giro completo
ci sono 2p radianti alloraÞ w=2pf .
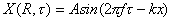 (7)
(7)
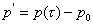 (8)
(8)
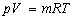
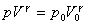 (9)
(9)
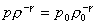 (10)
(10)
Quindi la pressione in
funzione della densità risulta essere:
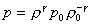 (11)
(11)
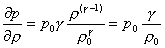 (12)
(12)
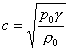 (13)
(13)
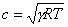 (14)
(14)
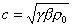
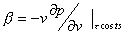 (15)
(15)
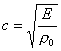 (16)
(16)
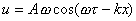 (17)
(17)
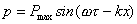 (18)
(18)