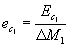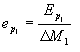Sistema aperto : bilancio massa e energia
Un sistema e` una
porzione di spazio delimitata da una superficie detta confine che puo` essere
chiusa, impedendo lo scambio di materia con l’esterno, tipica dei sistemi
chiusi che da essa prendono nome e che abbiamo fino ad ora trattato, o aperta
lasciando entrare e uscire materia attraverso zone dette rispettivamente
sezioni di ingresso e sezioni di uscita. La massa che fluisce all’interno di un
sistema aperto non si puo` generalmente considerare costante, nonostante che in
assoluto valga il principio di conservazione della massa secondo il quale la
massa dell’universo non dovrebbe cambiare nel tempo. In realta` tale principio
va rivisto attraverso la teoria relativistica fondata sulla legge di Einstein:
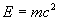 (1)
(1)
che ammette il consumo di massa a scapito di energia ( tale fenomeno e`
riscontrabile nelle stelle durante la fusione nucleare attraverso il processo protone-protone che trasforma idrogeno
in elio con perdita di massa e produzione di energia ). Tra massa ed energia
non esiste quindi distinzione. Tuttavia si puo` notare che il coefficiente di
proporzionalita` tra queste due grandezze e` pari alla velocita` della luce 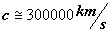 elevata al quadrato, cio` significa che ogni joule di energia equivale ad una massa infinitesima, di conseguenza
anche se si ha a che fare con sistemi che scambiano calore per i quali quindi
vale (1), l’errore che si commette non considerando lo scambio tra massa e
energia e` irrilevante ripetto ad errori di approssimazione e di calcolo. Trascurando
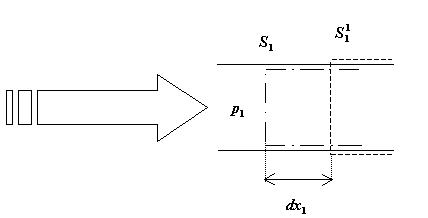
dunque la trasformazione di massa all’interno di un sistema aperto, lo si puo`
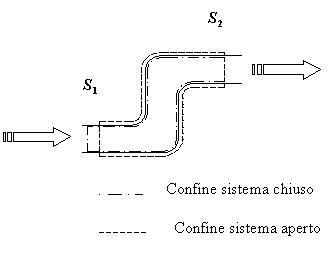
per semplicita` assimilare ad un condotto le cui superfici laterali sono
impermeabili e per il quale lo scambio di materia avviene attraverso due
sezioni: una di entrata
elevata al quadrato, cio` significa che ogni joule di energia equivale ad una massa infinitesima, di conseguenza
anche se si ha a che fare con sistemi che scambiano calore per i quali quindi
vale (1), l’errore che si commette non considerando lo scambio tra massa e
energia e` irrilevante ripetto ad errori di approssimazione e di calcolo. Trascurando
dunque la trasformazione di massa all’interno di un sistema aperto, lo si puo`
per semplicita` assimilare ad un condotto le cui superfici laterali sono
impermeabili e per il quale lo scambio di materia avviene attraverso due
sezioni: una di entrata 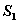 e una di uscita
e una di uscita 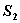 e lo scambio di lavoro per mezzo di un albero rotante che attraversa il
condotto (vd. Fig.1).
e lo scambio di lavoro per mezzo di un albero rotante che attraversa il
condotto (vd. Fig.1).
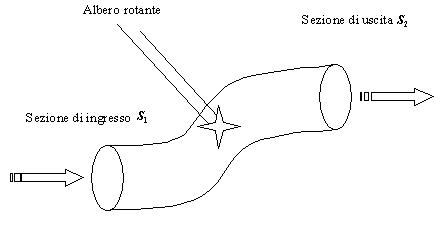
Sara` poi possibile estendere il
risultato ottenuto per questo modello semplificato a sistemi piu` complessi
dotati di un maggior numero di sezioni d’ingresso e di uscita
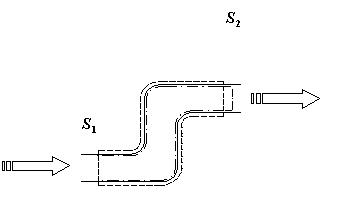
Per affrontare lo
studio del suddetto sistema semplificato si considera un sistema chiuso
ausiliario che si sposta nello spazio per il quale le proprieta` termodinamiche
non variano nel tempo, e una porzione fissa di spazio: il sistema aperto, che
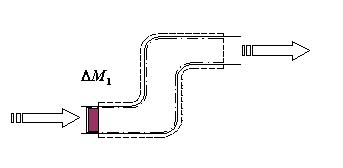
nel tempo viene attraversato dal sistema chiuso (vd Fig.2 e Fig.3).
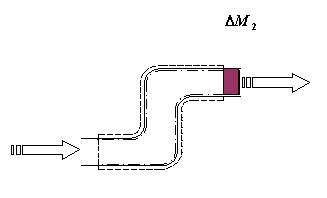
Mentre il sistema aperto e` stato interessato dall’entrata di una massa 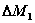 e dall’uscita di una massa
e dall’uscita di una massa 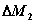 , il
sistema chiuso ausiliario, per definizione di sistema chiuso, ha conservato
nell’intervallo di tempo
, il
sistema chiuso ausiliario, per definizione di sistema chiuso, ha conservato
nell’intervallo di tempo 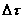 la stessa
massa pur avendo subito uno spostamento nello spazio. Si puo` quindi scrivere
un’ equazione di bilancio di massa per il sistema chiuso data da
la stessa
massa pur avendo subito uno spostamento nello spazio. Si puo` quindi scrivere
un’ equazione di bilancio di massa per il sistema chiuso data da
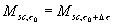 (3)
(3)
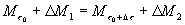 (4)
(4)
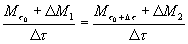 (5)
(5)
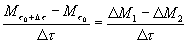 (6)
(6)
Il primo membro dell’equazione (6) rappresenta un rapporto incrementale
quindi, per definizione di derivata, facendo il limite per 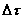 che tende a
zero si ottiene:
che tende a
zero si ottiene:
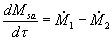 (7)
(7)
Nel caso piu`
generale in cui il sistema sia costituito da piu` sezioni di entrata e di
uscita la (7) assume la forma
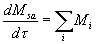 (8)
(8)
Se il sistema
aperto si trova in regime stazionario
cioe` se le sue proprieta` termodinamiche e meccaniche assumono in ogni punto
valori costanti nel tempo, la portata in massa che entra e` uguale alla portata
in massa che esce cioe`
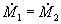 (9)
(9)
Bilancio dell’energia
E` possibile
calcolare l’equazione di bilancio dell’energia sfruttando la stessa
schematizzazione usata per il bilancio della massa riportata in Fig.3 e Fig.4.
Per 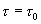 alla massa
contenuta nel sistema chiuso ausiliario e` associata un’energia pari a
alla massa
contenuta nel sistema chiuso ausiliario e` associata un’energia pari a
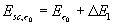 (10)
(10)
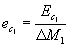 (11)
(11) 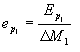 (12)
(12) 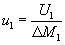 (13)
(13)
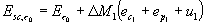 (14)
(14)
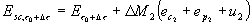 (15)
(15)
Se nell’intervallo
di tempo 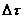 il sistema
chiuso ausiliario puo` modificare il proprio contenuto di energia solo per
mezzo di scambi di calore
il sistema
chiuso ausiliario puo` modificare il proprio contenuto di energia solo per
mezzo di scambi di calore 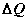 e di lavoro
e di lavoro 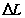 , alla sua
energia per
, alla sua
energia per 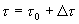 data da (15) devono essere aggiunti tali
contributi. Si puo` allora scrivere un’ equazione di bilancio energetico che
esprime il fatto che la variazione di energia nell’intervallo di tempo
data da (15) devono essere aggiunti tali
contributi. Si puo` allora scrivere un’ equazione di bilancio energetico che
esprime il fatto che la variazione di energia nell’intervallo di tempo 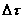 e` uguale
alla quantita` di energia scambiata sottoforma di calore e di lavoro. In altre
parole si applica il primo principio
della termodinamica per sistemi chiusi al sistema ausiliario
e` uguale
alla quantita` di energia scambiata sottoforma di calore e di lavoro. In altre
parole si applica il primo principio
della termodinamica per sistemi chiusi al sistema ausiliario
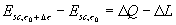 (16)
(16)
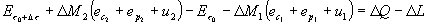 (17)
(17)
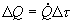 (18)
(18)
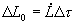 (19)
(19)
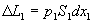 (20)
(20)
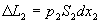 (21)
(21)
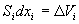 (22)
(22)
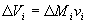 (23)
(23)
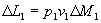 (24)
(24)
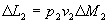 (25)
(25)
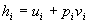 (27)
(27)
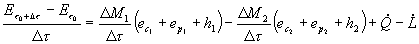 (28)
(28)
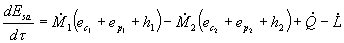 (29)
(29)
Nel caso di
regime stazionario il contenuto di energia e di massa del sistema rimangono
costanti quindi il primo membro si annulla, vale l’equazione (9), e definita
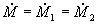 (30)
(30)
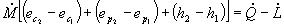 (31)
(31)
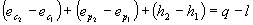 (32)
(32)
Calcolo
dell’energia cinetica
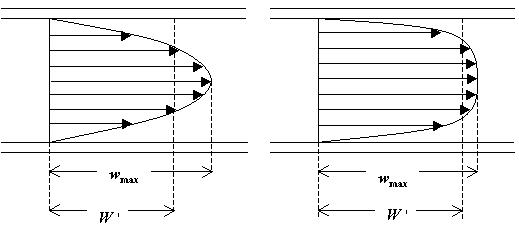
Per determinare
l’espressione dell’energia cinetica si deve considerare la sua dipendenza dalla
velocita` del fluido che attraversa il condotto. Tale velocita` non e` pero`
costante, ma varia in funzione della sezione che si prende in considerazione e
della distanza dall’asse del condotto. In atre parole dipende dal tipo di moto
che il fluido puo` assumere. All’interno del condotto infatti, il fluido non si
comporta come un corpo rigido per il quale l’energia cinetica vale:
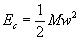 (33)
(33)
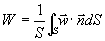 (34)
(34)
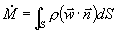 (35)
(35)
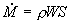 (36)
(36)
da cui e` possobile ricavare la portata
in volume
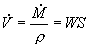 (37)
(37)
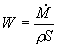 (38)
(38)
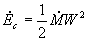 (39)
(39)
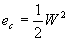 (40)
(40)
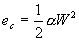 (41)
(41)
Calcolo
dell’energia potenziale
Per il calcolo
dell’energia potenziale, si fa riferimento ad un corpo di massa 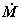 che si trova nel campo gravitazionale ad
un’altezza
che si trova nel campo gravitazionale ad
un’altezza 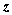 . Ad esso
e` associata una energia
. Ad esso
e` associata una energia
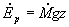 (42)
(42)
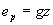 (43)
(43)
Sostituendo la (41) e la (43) nella (32) si ottiene:
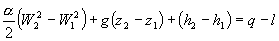 (44)
(44)
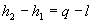 (45)
(45)
Ciclo di Rankine
Il ciclo di Rankine,
ciclo termodinamico per la produzione di energia, si realizza con la
successione di quattro apparecchiature: pompa, caldaia, turbina e condensatore
disposte come in Fig.9
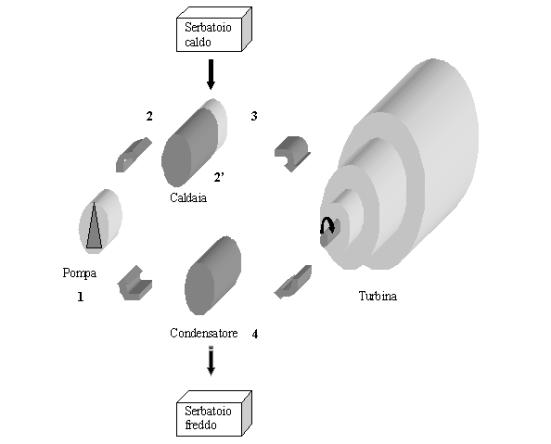
Fig.9
Il fluido che descrive il ciclo e` l’acqua che nella pompa passa da una
pressione inferiore a una superiore con relativo aumento di temperatura dovuto
pero` alla sola compressione (da 1 a
2), nella caldaia viene riscaldata e
vaporizzata a pressione costante fino a raggiungere lo stato di vapore saturo
secco prelevando calore dalla combustione di un combustibile e dell’aria
comburente (serbatoio caldo)(da 2 a 3). La turbina produce lavoro meccanico
a scapito del vapore che si espande adiabaticamente all’interno di apposite
palette (vd Fig.11a,b,c,d)(da 3 a 4) e il condesatore porta l’acqua dalla
fase di vapore a bassa pressione alla fase liquida attraverso una
trasformazione a temperatura e pressione costanti cedendo calore ad una
serpentina (serbatoio freddo)(da 4 a
1). I singoli componenti
si possono considerare dei sistemi aperti, quindi per il loro studio e`
possibile utilizzare la (45) in quanto non essendo in movimento, l’energia
cinetica e l’energia potenziale sono trascurabili. Se inoltre si ipotizzano
irrilevanti le perdite di carico e le dispersioni di calore che hanno luogo
lungo le condutture che collegano le diverse apparecchiature, gli stati fisici
del fluido all’uscita di un apparecchio e all’ingresso del successivo possono
essere considerati coincidenti. Si ottiene quindi il seguente ciclo (vd Fig.10)
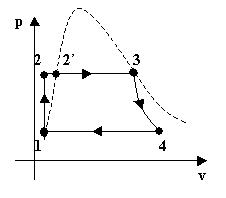
Fig.10
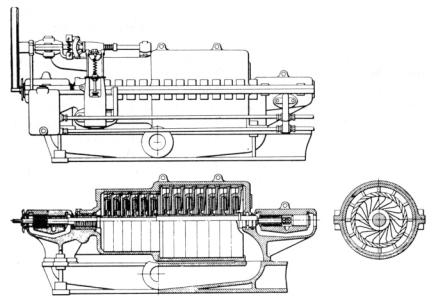
Fig.11a
Turbina a vapore

Fig.11b
Rotore di una turbina a doppio flusso

Fig.11c
Componenti di una turbina a doppio flusso in
fase di assemblaggio

Fig.11d
Il
rotore e una sezione del cilindro di una
turbina
![]() (1)
(1)![]() elevata al quadrato, cio` significa che ogni joule di energia equivale ad una massa infinitesima, di conseguenza
anche se si ha a che fare con sistemi che scambiano calore per i quali quindi
vale (1), l’errore che si commette non considerando lo scambio tra massa e
energia e` irrilevante ripetto ad errori di approssimazione e di calcolo. Trascurando
dunque la trasformazione di massa all’interno di un sistema aperto, lo si puo`
per semplicita` assimilare ad un condotto le cui superfici laterali sono
impermeabili e per il quale lo scambio di materia avviene attraverso due
sezioni: una di entrata
elevata al quadrato, cio` significa che ogni joule di energia equivale ad una massa infinitesima, di conseguenza
anche se si ha a che fare con sistemi che scambiano calore per i quali quindi
vale (1), l’errore che si commette non considerando lo scambio tra massa e
energia e` irrilevante ripetto ad errori di approssimazione e di calcolo. Trascurando
dunque la trasformazione di massa all’interno di un sistema aperto, lo si puo`
per semplicita` assimilare ad un condotto le cui superfici laterali sono
impermeabili e per il quale lo scambio di materia avviene attraverso due
sezioni: una di entrata ![]() e una di uscita
e una di uscita ![]() e lo scambio di lavoro per mezzo di un albero rotante che attraversa il
condotto (vd. Fig.1).
e lo scambio di lavoro per mezzo di un albero rotante che attraversa il
condotto (vd. Fig.1).