Strumenti per la misura della portata
Proseguiamo la nostra carrellata sui sistemi di misura della portata fluidodinamica nei condotti, iniziata nella lezione precedente.
Anemometro a filo caldo
L’anemometro a filo caldo è uno strumento per la misura della velocità puntuale di un fluido. Si tratta di un filo di platino percorso da una corrente elettrica nota ![]() , posto nel condotto in direzione trasversale rispetto al flusso del fluido.
, posto nel condotto in direzione trasversale rispetto al flusso del fluido.
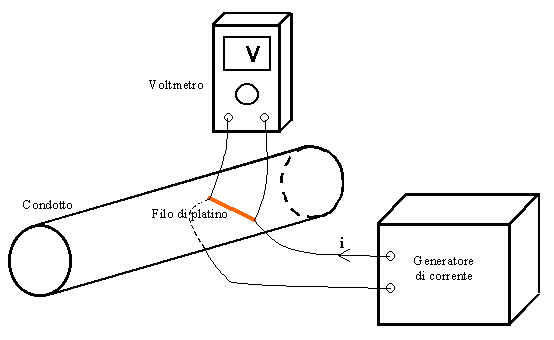
Figura 1 – Schema di principio dell’anemometro a filo di platino.
Il filo di platino è collegato ad un generatore di corrente tramite fili di rame dalla resistenza trascurabile, e presenta una resistenza ![]() che dipende dalla temperatura con una legge crescente:
che dipende dalla temperatura con una legge crescente:
![]() . (1)
. (1)
Il filo si riscalda a causa dell’effetto Joule; il calore prodotto è dato da
![]() . (2)
. (2)
Il flusso del fluido che investe il filo ne provoca un raffreddamento per convezione; la quantità di calore trasmessa dal filo al fluido ha un’espressione del tipo
![]() , (3)
, (3)
dove ![]() è la superficie esterna del filo,
è la superficie esterna del filo, ![]() è la differenza di temperatura tra il filo ed il fluido, e
è la differenza di temperatura tra il filo ed il fluido, e ![]() , detto comunemente coefficiente di convezione (anche se tale denominazione è sbagliata in quanto
, detto comunemente coefficiente di convezione (anche se tale denominazione è sbagliata in quanto ![]() non è adimensionale), è una complessa funzione di numerosi parametri, tra i quali la velocità del fluido
non è adimensionale), è una complessa funzione di numerosi parametri, tra i quali la velocità del fluido ![]() :
:
![]() . (4)
. (4)
A causa della complessità di tale dipendenza, essa è in genere fornita in forma tabellare piuttosto che in forma analitica.
Un voltmetro misura la tensione ![]() ai capi del filo di platino; questa misura permette di ricavare la resistenza
ai capi del filo di platino; questa misura permette di ricavare la resistenza ![]() tramite la legge di Ohm, dato che la corrente
tramite la legge di Ohm, dato che la corrente ![]() è nota:
è nota:
![]() . (5)
. (5)
Usando la relazione (1) inversa è così possibile risalire alla temperatura ![]() del filo di platino; dalle (2) e (3) si calcola il coefficiente di convezione
del filo di platino; dalle (2) e (3) si calcola il coefficiente di convezione ![]() del filo immerso nel fluido, ed invertendo la (4) si ricava finalmente la velocità
del filo immerso nel fluido, ed invertendo la (4) si ricava finalmente la velocità ![]() del fluido.
del fluido.
Come si vede il procedimento di misura richiede calcoli piuttosto complessi, comprendenti anche l’uso di tabelle. Quello riportato in fig. 1 è pertanto uno schema concettuale. Tutte le operazioni di calcolo e look-up di tabelle sono eseguite da un calcolatore, che contiene memorizzate al suo interno le tabelle relative alle relazioni (1) e (4). Il calcolatore controlla la corrente ![]() che scorre attraverso il filo, legge il valore della tensione
che scorre attraverso il filo, legge il valore della tensione ![]() ai suoi capi e della temperatura, esegue tutti i calcoli e presenta direttamente in forma numerica su un display il valore della velocità
ai suoi capi e della temperatura, esegue tutti i calcoli e presenta direttamente in forma numerica su un display il valore della velocità ![]() del fluido.
del fluido.
Anemometro laser-doppler
L’anemometro laser-doppler è uno strumento per la misura della velocità puntuale di un fluido.
Una sorgente laser produce un fascio di luce monocromatico. Un prisma formato da materiale cristallino birifrangente (che presenta cioè due distinti indici di rifrazione) sdoppia il fascio laser, producendo due fasci che presentano lunghezze d’onda identiche (fig. 2). Un sistema di lenti focalizza i due fasci laser facendoli convergere in un punto all’interno del fluido di cui si vuole misurare la velocità.
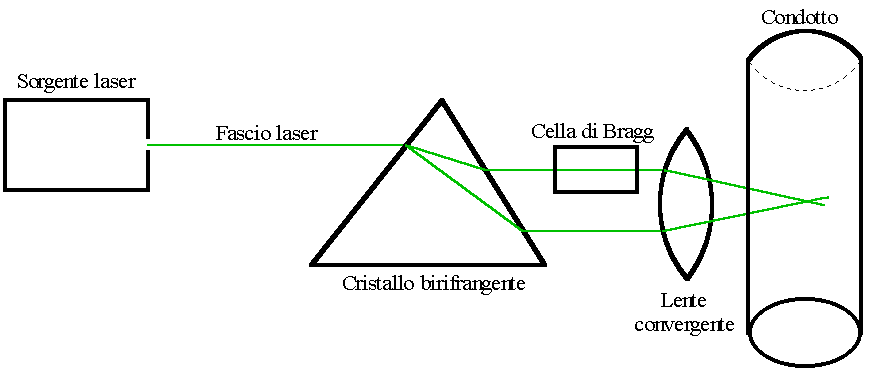
Figura 2 – Schema di principio dell’anemometro laser-doppler.
Per effettuare la misura è necessario che il fluido scorra in un tubo trasparente; per poter focalizzare i raggi laser a diverse profondità all’interno del fluido è inoltre necessario che il fluido stesso presenti una sufficiente trasparenza.
All’interno del fluido devono essere presenti in sospensione particelle riflettenti o fotoluminescenti, che riflettano o producano luce se illuminati da luce laser. E’ pratica comune per esempio aggiungere tracce di latte all’acqua che scorre in un tubo, in modo da aggiungere le particelle in sospensione necessarie al rilevamento della velocità.
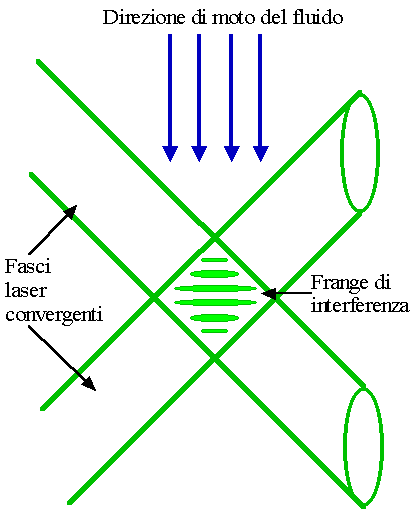
Figura 3 – Nella zona in cui i due raggi laser interagiscono si formano bande chiare e scure dette frange di interferenza.
Nel punto in cui i due fasci laser interagiscono si creano frange di interferenza, ovvero bande alternativamente buie e luminose dovute all’interferenza rispettivamente distruttiva e costruttiva della luce laser (fig. 3).
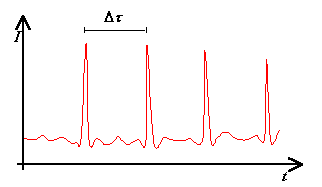
Figura 4 – Tipico andamento temporale dell’intensità luminosa I rilevata dal fotomoltiplicatore in un anemometro laser-doppler.
Un fotomoltiplicatore focalizzato sul punto d’incontro dei due fasci laser misura un picco di intensità luminosa ogni volta che una particella passa all’interno di una frangia di interferenza costruttiva. Un oscillogramma del segnale presente in uscita al fotomoltiplicatore presenta quindi picchi ad intervalli regolari al di sopra di un rumore di fondo sempre presente (fig. 4).
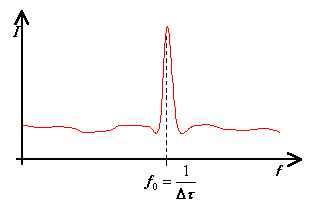
Figura 5 – Analisi spettrale del segnale di figura 4.
Detta ![]() la distanza, nota, tra due frange di interferenza costruttiva, il periodo di tali picchi vale
la distanza, nota, tra due frange di interferenza costruttiva, il periodo di tali picchi vale
![]() , (6)
, (6)
dove con ![]() indichiamo la velocità della particella in sospensione, e quindi del fluido che la trasporta.
indichiamo la velocità della particella in sospensione, e quindi del fluido che la trasporta.
Un’analisi spettrale del segnale in uscita dal fotomoltiplicatore (fig. 5) mostra un picco in corrispondenza della frequenza
![]() . (7)
. (7)
Il principale svantaggio di questo sistema di misurazione è che non è possibile discriminare il verso di scorrimento del fluido. Si ricorre allora ad una cella di Bragg sistemata lungo il percorso di uno dei due fasci laser (fig. 2). La cella di Bragg provoca uno shift (tipicamente pari a 40 MHz) sulla frequenza della radiazione laser. Questo provoca uno scorrimento delle frange di interferenza a 40 MHz; una particella ferma all’interno della zona di interferenza genera così picchi luminosi alla frequenza ![]() nel fotomoltiplicatore.
nel fotomoltiplicatore.
Quando il fluido, e con esso le particelle in sospensione, è in moto, interviene l’effetto doppler: se la particella si muove nello stesso verso delle frange di interferenza, incontrerà nell’unità di tempo un numero minore di zone ad interferenza costruttiva. La frequenza degli impulsi sarà pertanto minore di ![]() :
:
![]() . (8)
. (8)
Se invece il moto della particella avviene nel verso opposto al moto delle frange di interferenza, la frequenza del segnale in uscita al fotomoltiplicatore sarà maggiore di ![]() :
:
![]() , (9)
, (9)
dove in entrambi i casi ![]() è una quantità positiva che vale
è una quantità positiva che vale
![]() . (10)
. (10)
Con l’aggiunta della cella di Bragg si può quindi stimare il verso di moto del fluido nel condotto, ed inoltre si ha un segnale in uscita anche quando il fluido è fermo.
I principali svantaggi di questo sistema di misurazione sono l’elevato costo e la necessità di tempo e personale qualificato per la messa a punto.
Trasduttore ad effetto Coriolis
Il trasduttore ad effetto Coriolis è un misuratore di velocità media o di portata, molto usato in ambito industriale.
Un tubo che corre in direzione orizzontale, parallelo al piano x-y, presenta una zona a forma di "U" (fig. 6). Questa parte di tubo viene fatta vibrare lungo la direzione verticale z. Il fluido che scorre nel tubo è in questo modo soggetto alla forza di Coriolis, per effetto della rotazione della Terra; tale forza è direttamente proporzionale alla portata in massa del fluido nel condotto. Il fluido trasmette la sollecitazione al tubo, che subisce una deformazione. Misurando la deformazione del tubo è così possibile risalire alla portata in massa del fluido.
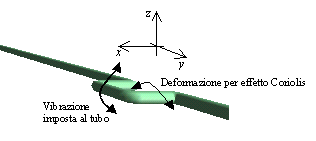
Figura 6 – Effetto della forza di Coriolis su un tubo percorso da un fluido.
La deformazione è misurata da un sistema di estensimetri (in inglese strain-gage). Un estensimetro è un trasduttore che presenta una resistenza elettrica proporzionale alla deformazione subita, e si presenta come una sorta di pezzo di nastro adesivo con un’area di qualche centimetro quadrato, che viene applicato direttamente sul condotto.
Prima della messa in funzione, il sistema di misurazione viene tarato facendo scorrere portate in massa note di fluido nel condotto, e misurando la resistenza corrispondente degli strain-gage.
Si tratta di un sistema economico, robusto e con accuratezza accettabile, che funziona indipendentemente dalla natura del fluido in esame. L’effetto Coriolis è massimo alla latitudine di 45°, ed è nullo all’equatore ed ai poli. Alle nostre latitudini quindi la sensibilità è pressoché massima.
Il misuratore di portata ad effetto Coriolis gode di largo impiego in ambiente industriale, dove non è raro vedere sezioni a forma di "U" nei tubi che corrono lungo le pareti.
Inserto – la forza di Coriolis
La forza di Coriolis fa parte di quelle forze fittizie che entrano in gioco quando si osservano i fenomeni fisici da sistemi di riferimento non inerziali. Un sistema di riferimento si dice inerziale se in esso un corpo non è accelerato (a=0) se non è influenzato da forze prodotte nel suo ambiente (S F=0).
Una giostra che gira costituisce un classico esempio di sistema di riferimento non inerziale, in quanto chi si trova su essa si muove allontanandosi dall’asse di rotazione, spinto dalla forza centrifuga. Per chi gira sulla giostra tenendo in mano una palla, questa sembra essere in equilibrio per il fatto che la forza centrifuga bilancia la forza della mano che la trattiene. Per un osservatore solidale con il suolo invece, la palla si muove di moto circolare ed ha un’accelerazione, diretta verso il centro della giostra, prodotta dalla forza centripeta che la mano esercita sulla palla. Per l’osservatore solidale con il suolo, poiché la palla non è in equilibrio ma è accelerata radialmente, non esiste forza centrifuga.
Supponiamo ora di metterci sul bordo della giostra che gira e di fare rotolare una palla verso l’interno, lungo una linea radiale disegnata sul pavimento della giostra. Nell’istante in cui la palla è lasciata andare a distanza r dall’asse, ha la velocità tangenziale (quella di chi la lancia) necessaria a fare un moto circolare di raggio r. Mentre si allontana verso il centro della giostra la palla, per mantenere una traiettoria radiale, dovrebbe via via diminuire la componente tangenziale della sua velocità. Poiché essa non ha modo di perdere la sua velocità tangenziale (si supponga trascurabile l’attrito tra il suolo e la palla), essa si muove un poco più avanti rispetto alla linea radiale dipinta. Più precisamente, nel sistema di riferimento non inerziale, bisogna supporre che esista una forza fittizia laterale, detta forza di Coriolis, che fa cambiare la direzione della palla dalla linea di rotolamento verso l’interno.
Per un osservatore solidale con un sistema inerziale la forza di Coriolis non esiste. La palla si muove lungo la linea retta determinata dalla direzione della velocità nell’istante in cui è stata lasciata andare.
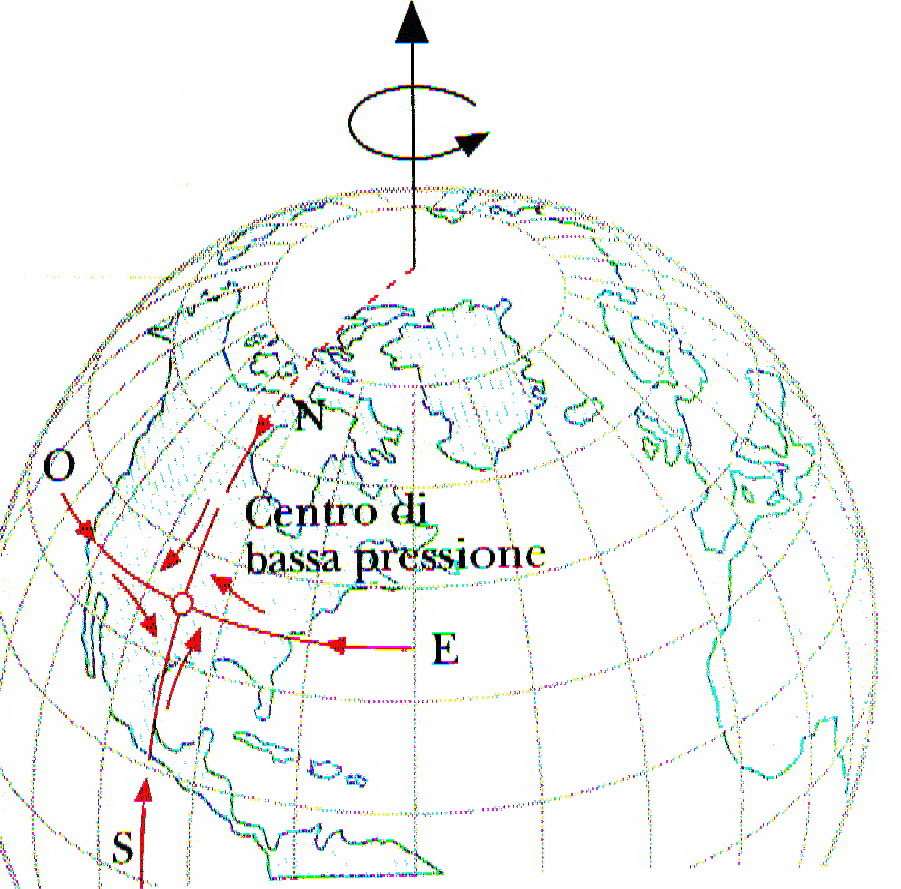
Figura 7 – Effetto della forza di Coriolis sulle masse d’aria intorno ad un centro di bassa pressione.
L’esempio più familiare della forza di Coriolis è rappresentato dal moto delle masse d’aria nell’atmosfera intorno ad un centro di bassa pressione. La figura 7 mostra un diagramma dei centri di bassa pressione nell’emisfero nord. Poiché in una certa zona la pressione è inferiore di quella circostante, l’aria fluisce radialmente verso l’interno della zona di bassa pressione da tutte le direzioni. Mentre la Terra ruota (per cui diventa un sistema non inerziale) produce sulle masse d’aria in moto effetti simili a quelli prodotti sulla palla dalla giostra girevole. L’aria che fluisce da sud, come la palla lanciata verso l’interno sulla giostra girevole, devia leggermente dalla linea immaginaria tracciata sulla Terra rotante, mentre l’aria che soffia da nord resta un po’ indietro rispetto a tale linea. L’effetto totale è che l’aria ruota in senso orario intorno alla zona di bassa pressione. La forza di Coriolis è quindi responsabile della circolazione dei venti nei cicloni e negli uragani. Nell’emisfero sud l’effetto è invertito.
Esercizi sul moto interno dei fluidi
Esercizio 1 - Autoclave
Un’autoclave è in linea di principio un serbatoio per l’acqua mantenuto ad una pressione maggiore della pressione atmosferica. E’ utilizzato negli impianti di riscaldamento di case a più piani, per permettere all’acqua calda di raggiungere i piani alti dell’abitazione, e negli impianti idraulici di case di campagna non servite dalla rete idrica municipalizzata.
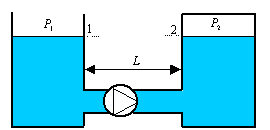
Figura 8 – Schema dell’esercizio 1
Nel nostro esercizio una pompa preleva acqua da un serbatoio e la immette in un’autoclave attraverso un condotto a sezione circolare (fig. 8).
Sono date la portata in massa ![]() , le pressioni
, le pressioni ![]() e
e ![]() all’interno del serbatoio e dell’autoclave, la lunghezza
all’interno del serbatoio e dell’autoclave, la lunghezza ![]() , il diametro
, il diametro ![]() e la rugosità relativa
e la rugosità relativa ![]() del tubo che collega il serbatoio all’autoclave. I peli liberi dell’acqua nel serbatoio e nell’autoclave si suppongano per semplicità fermi e alla stessa altezza. Si calcolino la prevalenza
del tubo che collega il serbatoio all’autoclave. I peli liberi dell’acqua nel serbatoio e nell’autoclave si suppongano per semplicità fermi e alla stessa altezza. Si calcolino la prevalenza ![]() e la potenza
e la potenza ![]() necessarie alla pompa per far funzionare l’autoclave.
necessarie alla pompa per far funzionare l’autoclave.
Dati del problema:
![]()
![]() ;
; ![]() m;
m; ![]() BAR;
BAR; ![]() BAR;
BAR; ![]() m;
m; ![]() ;
; ![]()
![]() ;
; ![]()
![]() .
.
Scriviamo l’equazione di Bernoulli tra due generiche sezioni 1 e 2:
![]() . (11)
. (11)
Come evidenziato in fig. 8, scegliamo come sezione 1 il pelo libero dell’acqua nel serbatoio, e come sezione 2 il pelo libero dell’acqua nell’autoclave. Questa scelta permette una notevole semplificazione dell’equazione di Bernoulli, dato che ![]() e
e ![]() :
:
![]() . (12)
. (12)
La velocità ![]() dell’acqua nel condotto è data da:
dell’acqua nel condotto è data da:
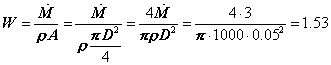
![]() , (13)
, (13)
dove ![]() è l’area della sezione del condotto.
è l’area della sezione del condotto.
Scriviamo ora l’espressione per le perdite per attrito ![]() . Utilizzando per le perdite concentrate la notazione con la lunghezza equivalente possiamo raggruppare perdite distribuite e concentrate:
. Utilizzando per le perdite concentrate la notazione con la lunghezza equivalente possiamo raggruppare perdite distribuite e concentrate:
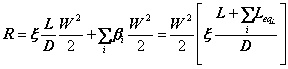 . (14)
. (14)
Le perdite concentrate sono relative all’imbocco ed allo sbocco del tubo. Utilizzando il nomogramma per il calcolo delle lunghezze equivalenti troviamo ![]() m,
m, ![]() m. Calcoliamo il numero di Reynolds
m. Calcoliamo il numero di Reynolds ![]() :
:
![]() (15)
(15)
Il moto è turbolento. Usiamo il numero di Reynolds per individuare il valore del fattore di attrito ![]() sul diagramma di Moody; otteniamo un valore
sul diagramma di Moody; otteniamo un valore ![]() .
.
Ora abbiamo a disposizione tutti i dati da inserire nella formula (14) per il calcolo del valore di ![]() :
:
![]()
![]() .
.
Dalla (12) ricaviamo la prevalenza necessaria alla pompa:
![]() BAR = 160000 Pa. (16)
BAR = 160000 Pa. (16)
La potenza richiesta alla pompa vale pertanto:
![]() W, (17)
W, (17)
dove ![]() è la portata in volume all’interno del condotto.
è la portata in volume all’interno del condotto.
Esercizio 2 - Fontana
Abbiamo una fontana (fig. 9) di cui conosciamo l’altezza ![]() del tubo, la prevalenza
del tubo, la prevalenza ![]() della pompa, il diametro
della pompa, il diametro ![]() del tubo, il diametro
del tubo, il diametro ![]() della sezione di sbocco, la rugosità media
della sezione di sbocco, la rugosità media ![]() del tubo. Calcolare l’altezza massima
del tubo. Calcolare l’altezza massima ![]() raggiunta dall’acqua rispetto alla sezione di sbocco della fontana.
raggiunta dall’acqua rispetto alla sezione di sbocco della fontana.
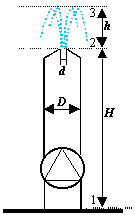
Figura 9 – Schema dell’esercizio 2
Dati del problema:
![]() BAR;
BAR; ![]() m;
m; ![]() m;
m; ![]() m;
m; ![]() mm;
mm; ![]()
![]() ;
; ![]()
![]() .
.
Scegliamo la sezione 1 alla base della fontana, la sezione 2 allo sbocco e la sezione 3 alla massima altezza raggiunta dall’acqua (fig. 9).
Appena prima dello sbocco il tubo presenta una forte riduzione di diametro, da ![]() a
a ![]() ; calcoliamo il rapporto tra le velocità del fluido nelle sezioni 1 e 2:
; calcoliamo il rapporto tra le velocità del fluido nelle sezioni 1 e 2:
![]() . (18)
. (18)
Riscriviamo quindi l’equazione di Bernoulli (11), notando che ![]() :
:
![]() . (19)
. (19)
Calcoliamo le perdite per attrito, utilizzando per l’unica perdita concentrata presente (il restringimento del tubo allo sbocco) la lunghezza equivalente. Dal nomogramma per le perdite concentrate troviamo ![]() m.
m.
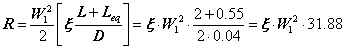
![]() . (20)
. (20)
Sostituendo la (20) nella (19) otteniamo
![]()
![]() , (21)
, (21)
da cui
![]() . (22)
. (22)
Per determinare i valori corretti di ![]() e di
e di ![]() dobbiamo ora procedere per tentativi, prendendo un valore probabile di
dobbiamo ora procedere per tentativi, prendendo un valore probabile di ![]() e calcolando il corrispondente valore di
e calcolando il corrispondente valore di ![]() , e reiterando il processo fino a che valori non si stabilizzano.
, e reiterando il processo fino a che valori non si stabilizzano.
Notiamo che al denominatore della (22) il valore di ![]() assumerà tipicamente valori inferiori di qualche ordine di grandezza rispetto al termine di confronto 127.5; scegliamo pertanto come valore di prova di
assumerà tipicamente valori inferiori di qualche ordine di grandezza rispetto al termine di confronto 127.5; scegliamo pertanto come valore di prova di ![]() quello dato dalla (22) per
quello dato dalla (22) per ![]() , che presumibilmente sarà molto vicino al valore di
, che presumibilmente sarà molto vicino al valore di ![]() corretto:
corretto:
![]()
![]() . (23)
. (23)
Il numero di Reynolds corrispondente vale
![]() (24)
(24)
Per utilizzare il diagramma di Moody occorre calcolare la rugosità relativa:
![]() . (25)
. (25)
Dal diagramma di Moody ricaviamo un coefficiente di attrito ![]() pari a 0,027. Questo valore, sostituito nella (22), fornisce un valore di seconda iterazione per
pari a 0,027. Questo valore, sostituito nella (22), fornisce un valore di seconda iterazione per ![]() :
:
![]()
![]() . (26)
. (26)
Data la differenza trascurabile tra ![]() e
e ![]() assumiamo quest’ultimo come il valore corretto per
assumiamo quest’ultimo come il valore corretto per ![]() . Dalla (18) si ricava
. Dalla (18) si ricava
![]()
![]() . (27)
. (27)
Scriviamo ora l’equazione di Bernoulli tra le sezioni 2 e 3, tenendo conto che ![]() (l’acqua è istantaneamente ferma quando raggiunge la massima quota),
(l’acqua è istantaneamente ferma quando raggiunge la massima quota), ![]() e
e ![]() sono entrambe uguali alla pressione atmosferica,
sono entrambe uguali alla pressione atmosferica, ![]() trascurando le perdite per attrito (
trascurando le perdite per attrito (![]() ) e sapendo che l’acqua non riceve lavoro dall’esterno:
) e sapendo che l’acqua non riceve lavoro dall’esterno:
![]() , (28)
, (28)
da cui si ricava
![]() m. (29)
m. (29)
Esercizio 3 – Serbatoio che si svuota
Ad un serbatoio cilindrico pieno d’acqua viene tolto il tappo, posto sul fondo. Dal foro sul fondo inizia a fuoriuscire l’acqua (fig. 10). Del serbatoio si conosce l’altezza ![]() , il diametro
, il diametro ![]() , e il diametro
, e il diametro ![]() del foro circolare da cui l’acqua fuoriesce. Calcolare il tempo
del foro circolare da cui l’acqua fuoriesce. Calcolare il tempo ![]() impiegato dal serbatoio per vuotarsi completamente.
impiegato dal serbatoio per vuotarsi completamente.
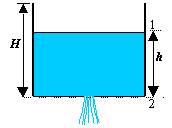
Figura 10 – Schema dell’esercizio 3
Dati del problema:
![]() m;
m; ![]() m;
m; ![]() m.
m.
Chiamiamo ![]() l’altezza del pelo libero dell’acqua misurata rispetto alla base del serbatoio, variabile nel tempo, e scegliamo la sezione 1 coincidente col pelo libero (quindi anch’essa variabile nel tempo), e la sezione 2 corrispondente al foro d’uscita.
l’altezza del pelo libero dell’acqua misurata rispetto alla base del serbatoio, variabile nel tempo, e scegliamo la sezione 1 coincidente col pelo libero (quindi anch’essa variabile nel tempo), e la sezione 2 corrispondente al foro d’uscita. ![]() varia con andamento monotono decrescente nel tempo da un valore massimo
varia con andamento monotono decrescente nel tempo da un valore massimo ![]() , assunto per
, assunto per ![]() , fino ad assumere valore 0 per
, fino ad assumere valore 0 per ![]() .
.
L’acqua incontra nel suo percorso la sola perdita di carico concentrata corrispondente al restringimento della sezione allo sbocco, che determina un fattore di attrito ![]() . Date le grandi dimensioni del serbatoio, la velocità
. Date le grandi dimensioni del serbatoio, la velocità ![]() del fluido al suo interno sarà molto ridotta; trascuriamo pertanto le perdite di carico distribuite, che oltretutto complicherebbero oltremodo il problema dato che
del fluido al suo interno sarà molto ridotta; trascuriamo pertanto le perdite di carico distribuite, che oltretutto complicherebbero oltremodo il problema dato che ![]() non è costante nel tempo:
non è costante nel tempo:
![]() . (30)
. (30)
Dato che conosciamo il rapporto tra le dimensioni delle sezioni 1 e 2, calcoliamo il rapporto tra le velocità dell’acqua nelle sezioni 1 e 2:
![]() . (31)
. (31)
Riscriviamo l’equazione di Bernoulli (11) adattandola al nostro caso, notando che ![]() e
e ![]() sono entrambe uguali alla pressione atmosferica, che
sono entrambe uguali alla pressione atmosferica, che ![]() , che l’acqua non riceve lavoro dall’esterno, e sostituendo ad
, che l’acqua non riceve lavoro dall’esterno, e sostituendo ad ![]() l’espressione (30):
l’espressione (30):
![]() (32)
(32)
Sostituendo nella (32) la (31) e gli appropriati valori numerici otteniamo:
![]() , da cui si ricava (33)
, da cui si ricava (33)
![]() . (34)
. (34)
La velocità ![]() non è altro che la velocità con cui il pelo libero dell’acqua si muove verso il basso nel serbatoio mentre questo si svuota:
non è altro che la velocità con cui il pelo libero dell’acqua si muove verso il basso nel serbatoio mentre questo si svuota:
![]() , (35)
, (35)
da cui otteniamo, sostituendo la (34) nella (35)
![]() . (36)
. (36)
Separiamo le variabili ed integriamo per ![]() che varia tra
che varia tra ![]() e 0, e per
e 0, e per ![]() che varia tra 0 e
che varia tra 0 e ![]() :
:
![]() , (37)
, (37)
da cui ricaviamo
![]() . (38)
. (38)
Si ottiene infine
![]() s. (39)
s. (39)
Esiste una variante di questo esercizio, in cui il serbatoio si svuota attraverso un tubo di lunghezza L (fig. 11). Questa variante sarà trattata in una delle prossime lezioni.
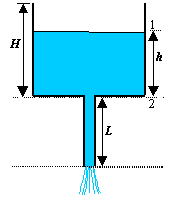
Figura 11 – Variante dell’esercizio 3