Introduzione
*Proprietà termodinamiche (p, v, T)
*Grafici
*Diagrammi (p,v) e (p,T)
*Equilibrio L-V
*Vapore surriscaldato
*Liquido sottoraffreddato
*Entropia del liquido
*Appendice
*
Questa lezione si propone di chiarire cosa si intende per sistema chimicamente omogeneo. Ci troviamo nella categoria dei sistemi chiusi, la cui massa quindi non varia.
Dal punto di vista della regola delle fasi di Gibbs vuol dire che il numero delle componenti c è uguale a 1. Ricordiamo tale formula:
V = C – F + 2
Dove V rappresenta la varianza (ossia le variabili che possono subire variazioni senza alterare il numero e il tipo delle fasi presenti in un sistema eterogeneo); C è il numero di componenti chimici indipendenti ed F il numero delle fasi presenti.
Il fatto che C=1 può essere il risultato di due diverse situazioni:
79% N2 Azoto
21% O2 Ossigeno
In realtà l’aria non è da considerarsi un sistema chimicamente omogeneo a tutti gli effetti. D’altra parte però nella maggior parte dei problemi che si affronteranno in questo corso, siccome si lavorerà a temperature discretamente elevate e pressioni relativamente basse, non c’è modo di distinguere le differenze tra questi due gas. Per questo possiamo considerare l’aria un sistema chimicamente omogeneo. Attenzione però: questa approssimazione ha senso solo nelle condizioni appena citate; se ci si trova vicini alla temperatura ambiente tutto questo cade!!!
Per questa lezione considereremo l’aria come un sistema non chimicamente omogeneo.
Passiamo ora a valutare le proprietà termodinamiche.
Proprietà termodinamiche (p, v, T)
I legami matematici che si instaurano tra queste grandezze danno luogo alle cosiddette equazioni di stato. Dalla formula di Gibbs segue che se C=1 e F=1 la varianza V=2. Allora in queste equazioni solo 2 variabili sono indipendenti: la terza è individuata univocamente dalle altre due. Molte volte però, a causa di calcoli eccessivamente complessi, non si riesce a determinare la terza grandezza. In nostro aiuto ci vengono le tabelle e i grafici.
Oltre le tre grandezze fondamentali p, v, T , risultano essere utilissime anche la entalpia specifica h, l’ energia interna specifica u e l’ entropia specifica s.
Sono i classici grafici cartesiani bidimensionali. I più utilizzati sono i seguenti:

Fig.1 Principali grafici bidimensionali utilizzati.
Con queste quattro caratteristiche si possono descrivere i comportamenti di qualsiasi sostanza che si trovi allo stato puro (cioè costituita da elementi chimicamente puri). Ciascuno di questi quattro grafici è il risultato della proiezione sugli assi corrispondenti di un grafico 6-dimensionale (p,v,t,u,h,s).
Quando il sistema presenta una variazione non nulla tra una grandezza e l’altra vuol dire che esiste un angolo tra due assi. Siccome esistono casi in cui due assi possono coincidere non riesco in questo caso a disegnare sulla proiezione bidimensionale il punto in esame.
Limitiamoci per ora allo spazio tridimensionale individuato dalla terna (p,v,T):
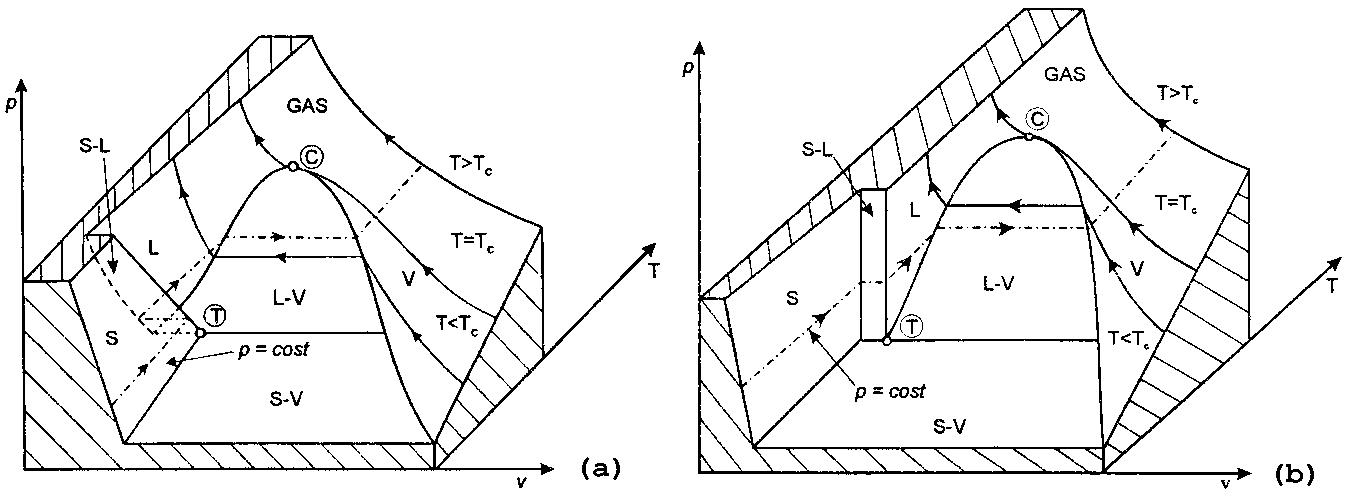
Fig.2 Diagramma collinare tipico di sostanze con comportamenti simili all’acqua (a), simili all’olio (b).
Nella Fig.2a è descritto il particolare comportamento dell’acqua. Su questa superficie giacciono tutti i possibili stati fisici. Si denotano due punti rilevanti:
Nella zona a volume costante e a temperature inferiori a quelle del punto triplo si trova il solido.
Dove il numero delle fasi F=2 si hanno tutte le zone di equiulibrio tra S-V, S-L,
L-V. Ricordiamoci che alle temperature di equilibrio tra due fasi, ciascuna delle due fasi può esistere; la grandezza che in un certo senso decide quale delle due prevale rispetto all’altra è l’energia. Classico esempio è l’equilibrio H2O – ghiaccio.
Per quanto riguarda la Fig.2b il ragionamento è analogo, l’unica differenza è che in questo caso la sostanza in gioco fondendo aumenta di volume, mentre nella solidificazione diminuisce di volume. Quindi le diversità sostanziali stanno nel punto triplo, caratterizzato da un comportamento opposto a quello delle sostanze come l’acqua.
Ecco una tabella che riporta i valori di temperatura e pressione al punto triplo e al punto critico per alcune delle più usate sostanze:
|
Punto triplo |
Punto critico |
|||
|
Sostanze |
TT (K) |
PT (bar) |
TC (K) |
PC (bar) |
|
Acqua (H2O) |
273,16 |
0,611× 10-3 |
647,25 |
221,19 |
|
Ammoniaca (NH3) |
195,40 |
6,081 × 10-3 |
405,65 |
113,99 |
|
Anidride carbonica (CO2) |
216,55 |
5,11 |
304,15 |
73,87 |
|
Anidride solforosa (SO2) |
197,68 |
0,167 × 10-3 |
430,95 |
78,73 |
|
Azoto (N2) |
63,18 |
12,53 × 10-3 |
126,15 |
33,94 |
|
Neon (Ne) |
24,57 |
43,20 × 10-3 |
44,45 |
27,26 |
|
Ossigeno (O2) |
54,35 |
0,152 × 10-3 |
154,75 |
50,76 |
Uno dei diagrammi più utilizzati è il (p,v):
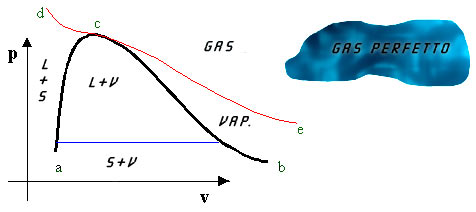
Fig.3
Diagramma (p,v).
Nella "nuvola" del gas perfetto le relazioni tra p,v,T sono sintetizzate dalla equazione di stato : pv= RT. Le cose si complicano all’esterno di questa zona.In generale come ben sappiamo il comportamento dei gas reali è trattato in maniera diversa da quello dei gas ideali. Infatti quando ci troviamo a pressioni relativamente elevate e temperature relativamente basse, le forze d'attrazione intermolecolari ed il volume proprio delle molecole non possono più essere trascurati, perciò la semplice relazione p× v = R× T necessita da qualche modifica che tenga conto di queste variazioni di comportamento. Per nostra fortuna noi lavoreremo quasi sempre nel campo dei gas ideali, oppure considereremo trascurabili tali variazioni.
Per meglio distinguere le zone appartenenti alle tre fasi possibili si utilizzano diagrammi (p,T). Le tre curve sono le cosiddette curve d’equilibrio. Particolarmente interessante è quella d’equilibrio S-L. Si denota facilmente che la temperatura del punto di fusione del ghiaccio è inferiore a quella del punto triplo dell’acqua. Invece per la maggior parte delle sostanze la temperatura relativa al cambiamento di fase S-L risulta maggiore del punto triplo.
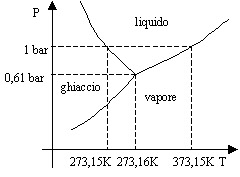
Fig.4 Diagramma di stato dell’acqua.
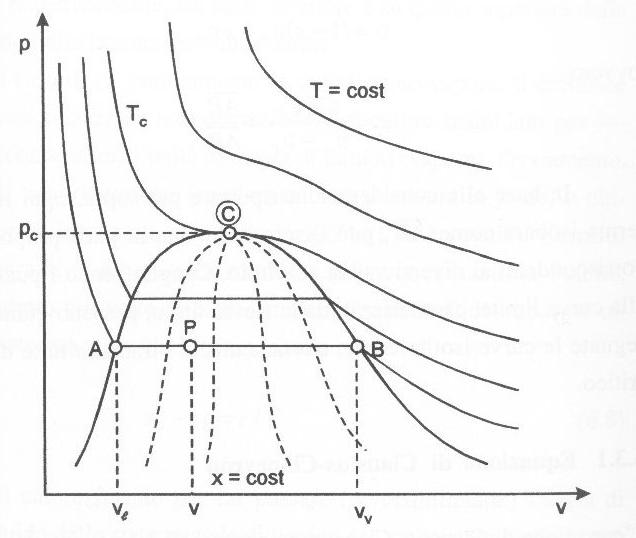
Fig.5 Diagramma (p,v) con, in tratteggiato, le curve a titolo costante.
Si può notare con chiarezza che l’isoterma fondamentale (critica) separa la zona dei vapori da quella dei gas. Al di sopra della temperatura critica vi è completa continuità tra gli stati, in quanto entrambi gli stati liquido e gassoso hanno struttura disordinata. Questa continuità non esiste fra stato liquido e stato solido perché non è possibile trasformare gradualmente uno stato disordinato in uno ordinato.
Sotto la campana di Andrews giacciono gli equilibri L-V, ovvero vapori saturi. Una particolarità si ha proprio in questa zona; qui le isobare e le isoterme coincidono. Per maggior chiarezza si usa introdurre una nuova grandezza, il titolo, definita come il rapporto tra la massa del vapore e la massa totale:
![]()
Da come è definito è facile dedurre che :
Il titolo è stato introdotto perché esso è una variabile indipendente, mentre sotto la campana di Andrews temperatura e pressione sono tra loro degeneri (l’una individua l’altra), inoltre è molto comodo dal punto di vista dei calcoli; infatti fissato un punto su un generico segmento di isobara/isoterma, il titolo si determina facendo il rapporto tra i due segmenti contigui.
|
Consideriamo per esempio che : Mtot = 1 Kg , x = 0,4 Þ |
Mvap = x× Mtot = 0,4 Kg Mliq = 1 – x× Mtot = 0,6 Kg V = [(1 – x) vliq + x × vvap]× Mtot |
In realtà è più facile trovare tabellato al posto di vvap , vd (volume specifico differenziale), definito rispettivamente come la differenza tra i volumi specifici del vapore e del liquido.
Quindi fissato un punto generico w Þ v(w) = vliq + x × vd
In generale le grandezze termodinamiche che si possono trovare sulle tabelle sono le seguenti: T, p, vl ,vd ,ul , ud ,hl ,hd ,sl ,sd . Tra poco ci accorgeremo che grazie ad alcune relazioni, ci serviranno solo alcune di queste grandezze per delineare lo stato di equilibrio L-V.
L’ entalpia specifica differenziale hd è definita come la quantità di calore che è necessario fornire ad 1Kg di liquido per farlo diventare 1Kg di vapore. Scriviamo il 1º principio della termodinamica nelle due forme che conosciamo:
u2 – u1 = q – p × D v
h2 – h1 = q + v × D p = q
(p = cost.)La grandezza hd prende il nome di calore latente di vaporizzazione e si indica con r.
Per quando riguarda sd non è tabellata perché la si può ricavare dalla seguente relazione:
![]()
Solitamente sl è tabellata al posto di sd .
Riportiamo lo schema delle relazioni valide per lo studio delle proprietà del vapore saturo:
vx = vl + x× vd
ux = ul + x× (r - p× vd)
hx = hl + x× r
sx = sl + x× (r/T)
Importante è il fatto che nel campo dei liquidi i valori dei calori specifici (a pressione e a volume costante) sono praticamente uguali perciò:
cp = cv = cl
e quindi:
ul @ hl @ cl × t @ cl × (T – T0 )
dove t è espressa in Celsius e T0 = 273,15 K.
Nella fig.5 si possono notare all’interno della curva limite, le curve a titolo costante (quelle tratteggiate).
Sono i vapori che si trovano nella zona compresa tra la curva limite superiore e l’isoterma critica. Attenzione che il termine surriscaldato non si riferisce al valore assoluto della termperatura, infatti si possono trovare vapori surriscaldati anche a temperature del tutto ordinarie. Classico esempio è il vapor d’acqua che si trova nell’aria che noi respiriamo: esso è il più delle volte un vapore surriscaldato!
Si trovano nella zona compresa tra l’asse delle ordinate, la curva limite inferiore e l’isoterma critica. Sottoraffreddato sta a significare che il liquido si trova a pressioni più elevate del liquido saturo che si trova sulla stessa curva isotermica. Quindi anche in questo caso non bisogna fare confusione col concetto di temperatura. Esistono infatto liquidi che si trovano a temperature molto superiori di quella ambiente che vengono chiamati sempre sottoraffreddati.
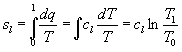
Giunti in conclusione possiamo dire che le vere grandezze termodunamiche che è utile trovare tabellate sono T, p, vd, r, cl. Le altre si possono tranquillamente ricavare dalle relazione che abbiamo ricavato durante questa lezione.
Tab1:Vapori saturi
|
T (ºC) |
Press. (kPa) |
vl (m3/kg) |
vg (m3/kg) |
hl (kJ/kg) |
hg (kJ/kg) |
sl kJ/kg× K |
sg kJ/kg× K |
|
0,01 |
0,6113 |
0,001000 |
206,14 |
0,01 |
2501,3 |
0 |
9,1562 |
|
5 |
0,8721 |
0,001000 |
147,12 |
20,98 |
2510,6 |
0,0761 |
9,0257 |
|
10 |
1,2276 |
0,001000 |
106,38 |
42,01 |
2519,8 |
0,151 |
8,9008 |
|
15 |
1,7051 |
0,001001 |
77,93 |
62,99 |
2528,9 |
0,2245 |
8,7814 |
|
20 |
2,339 |
0,001002 |
57,79 |
83,96 |
2538,1 |
0,2966 |
8,6672 |
|
25 |
3,169 |
0,001003 |
43,96 |
104,89 |
2547,2 |
0,3674 |
8,558 |
|
30 |
4,246 |
0,001004 |
32,89 |
125,79 |
2556,3 |
0,4369 |
8,4533 |
|
35 |
5,628 |
0,001006 |
25,22 |
146,68 |
2565,3 |
0,5053 |
8,3531 |
|
40 |
7,384 |
0,001008 |
19,52 |
167,57 |
2574,3 |
0,5725 |
8,257 |
|
45 |
9,593 |
0,001010 |
15,26 |
188,45 |
2583,2 |
0,6387 |
8,1648 |
|
50 |
12,349 |
0,001012 |
12,03 |
209,33 |
2592,1 |
0,7038 |
8,0763 |
|
55 |
15,758 |
0,001015 |
9,568 |
230,23 |
2600,9 |
0,7679 |
7,9913 |
|
60 |
19,94 |
0,001017 |
7,671 |
251,13 |
2609,6 |
0,8312 |
7,9096 |
|
65 |
25,03 |
0,001020 |
6,197 |
272,06 |
2618,3 |
0,8935 |
7,831 |
|
70 |
31,19 |
0,001023 |
5,042 |
292,98 |
2626,8 |
0,9549 |
7,7553 |
|
75 |
38,58 |
0,001026 |
4,131 |
313,93 |
2635,3 |
1,0155 |
7,6824 |
|
80 |
47,83 |
0,001029 |
3,407 |
334,91 |
2643,7 |
1,0753 |
7,6122 |
|
85 |
57,83 |
0,001033 |
2,828 |
355,9 |
2651,9 |
1,1343 |
7,5445 |
|
90 |
70,14 |
0,001036 |
2,361 |
376,92 |
2660,1 |
1,1925 |
7,4791 |
|
95 |
84,55 |
0,001040 |
1,982 |
397,96 |
2668,1 |
1,25 |
7,4159 |
|
100 |
101,42 |
0,001043 |
1,6718 |
419,16 |
2675,44 |
1,3072 |
7,3536 |
|
105 |
120,908 |
0,001047 |
1,4134 |
440,27 |
2683,26 |
1,3633 |
7,2946 |
|
110 |
143,39 |
0,001052 |
1,2093 |
461,41 |
2690,93 |
1,4188 |
7,2375 |
|
115 |
169,192 |
0,001056 |
1,0359 |
482,59 |
2698,46 |
1,4737 |
7,1822 |
|
120 |
198,835 |
0,001060 |
0,8912 |
503,81 |
2075,83 |
1,5279 |
7,1286 |
|
125 |
239,496 |
0,001066 |
0,7452 |
529,33 |
2714,44 |
1,5922 |
7,1664 |
|
130 |
270,306 |
0,001070 |
0,668 |
546,39 |
2720,04 |
1,6347 |
7,0261 |
|
135 |
322,479 |
0,001076 |
0,5662 |
572,03 |
2728,22 |
1,6977 |
6,9673 |
|
140 |
361,572 |
0,001080 |
0,5085 |
589,18 |
2733,51 |
1,7393 |
6,9292 |
|
145 |
427,306 |
0,001086 |
0,4347 |
614,97 |
2741,19 |
1,8011 |
6,8734 |
|
150 |
476,207 |
0,001091 |
0,3925 |
632,21 |
2746,13 |
1,8419 |
6,8372 |
|
155 |
557,882 |
0,001097 |
0,3381 |
658,16 |
2753,26 |
1,9025 |
6,7842 |
|
160 |
613,283 |
0,001102 |
0,3069 |
675,52 |
2757,82 |
1,9427 |
6,7497 |
|
165 |
713,546 |
0,001109 |
0,2662 |
701,65 |
2764,35 |
2,0023 |
6,699 |
|
170 |
792,245 |
0,001114 |
0,2427 |
719,14 |
2768,48 |
2,0418 |
6,6659 |
|
175 |
913,586 |
0,001122 |
0,2118 |
745,48 |
2774,33 |
2,1005 |
6,6173 |
|
180 |
1002,86 |
0,001127 |
0,1939 |
763,12 |
2777,99 |
2,1394 |
6,5854 |
|
185 |
1149,01 |
0,001136 |
0,1702 |
789,69 |
2783,1 |
2,1973 |
6,5354 |
|
190 |
1225,37 |
0,001141 |
0,1564 |
807,5 |
2786,23 |
2,2356 |
6,5076 |
|
195 |
1429,2 |
0,001150 |
0,138 |
834,34 |
2790,52 |
2,2928 |
6,4621 |
|
200 |
1555,1 |
0,001157 |
0,1272 |
852,33 |
2793,09 |
2,3307 |
6,4321 |
|
215 |
2,104 |
0,001181 |
0,0947 |
920,62 |
1879,9 |
2,4714 |
6,3221 |
|
220 |
2,318 |
0,001190 |
0,0862 |
943,62 |
1858,5 |
2,5178 |
6,2861 |
|
225 |
2,548 |
0,001199 |
0,0785 |
966,78 |
1836,5 |
2,5639 |
6,2503 |
|
230 |
2,795 |
0,001209 |
0,0716 |
990,12 |
1813,8 |
2,6099 |
6,2146 |
|
235 |
3,060 |
0,001219 |
0,0654 |
1013,62 |
1790,5 |
2,6558 |
6,1791 |
|
240 |
3,344 |
0,001229 |
0,0598 |
1037,32 |
1766,5 |
2,7015 |
6,1437 |
|
245 |
3,648 |
0,001240 |
0,0547 |
1061,23 |
1741,7 |
2,7472 |
6,1083 |
|
250 |
3,973 |
0,001251 |
0,0501 |
1085,36 |
1716,2 |
2,7927 |
6,0730 |
|
255 |
4,319 |
0,001263 |
0,0459 |
1109,73 |
1689,8 |
2,8383 |
6,0375 |
|
260 |
4,688 |
0,001276 |
0,0422 |
1134,37 |
1662,5 |
2,8838 |
6,0019 |
|
265 |
5,081 |
0,001289 |
0,0387 |
1159,28 |
1634,4 |
2,9294 |
5,9662 |
|
270 |
5,499 |
0,001302 |
0,0356 |
1184,51 |
1605,2 |
2,9751 |
5,9301 |
|
275 |
5,942 |
0,001317 |
0,0328 |
1210,07 |
1574,9 |
3,0208 |
5,8938 |
|
280 |
6,412 |
0,001332 |
0,0302 |
1235,99 |
1543,6 |
3,0668 |
5,8571 |
|
285 |
6,909 |
0,001348 |
0,0278 |
1262,31 |
1511,0 |
3,1130 |
5,8199 |
|
290 |
7,436 |
0,001336 |
0,0256 |
1289,07 |
2766,2 |
3,1594 |
5,7821 |
|
295 |
7,993 |
0,001384 |
0,0235 |
1316,3 |
2758,1 |
3,2062 |
5,7437 |
|
300 |
8,581 |
0,001404 |
0,0217 |
1344,0 |
2749,0 |
3,2534 |
5,7045 |
|
305 |
9,2202 |
0,001425 |
0,0199 |
1372,4 |
2738,1 |
3,3010 |
5,6643 |
|
310 |
9,856 |
0,001447 |
0,0183 |
1401,3 |
2727,3 |
3,3493 |
5,6230 |
|
315 |
10,547 |
0,001472 |
0,0168 |
1431,0 |
2714,5 |
3,3982 |
5,5804 |
|
320 |
11,274 |
0,001499 |
0,0155 |
1461,5 |
2700,1 |
3,4480 |
5,5362 |
|
330 |
12,845 |
0,001561 |
0,0129 |
1525,3 |
2665,9 |
3,5507 |
5,4417 |
|
340 |
14,586 |
0,001638 |
0,0108 |
1594,2 |
2622,0 |
3,6594 |
5,3357 |
|
350 |
16,513 |
0,001740 |
0,0088 |
1670,6 |
2563,9 |
3,7777 |
5,2112 |
|
360 |
18,651 |
0,001839 |
0,0069 |
1760,5 |
2481,0 |
3,9147 |
5,0526 |
|
370 |
21,03 |
0,002213 |
0,0049 |
1890,5 |
2332,1 |
4,1106 |
4,7971 |
|
374,14 |
22,09 |
0,003155 |
0,003155 |
2099,3 |
2099,3 |
4,4298 |
4,4298 |
Tab2: Vapori surriscaldati.
P = 1 BAR
|
T(ºC) |
v (m3/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg × K) |
|
Sat. |
1,694 |
2506,1 |
2675,5 |
7,3594 |
|
100 |
1,696 |
2506,7 |
2676,2 |
7,3614 |
|
150 |
1,936 |
2582,8 |
2776,4 |
7,6134 |
|
200 |
2,172 |
2658,1 |
2875,3 |
7,8343 |
|
250 |
2,406 |
2733,7 |
2974,3 |
8,0333 |
|
300 |
2,639 |
2810,4 |
3074,3 |
8,2158 |
|
400 |
3,103 |
2967,9 |
3278,2 |
8,5435 |
|
500 |
3,565 |
3131,6 |
3488,1 |
8,8342 |
|
600 |
4,028 |
3301,9 |
3704,7 |
9,0976 |
|
700 |
4,490 |
3479,2 |
3928,2 |
9,3398 |
|
800 |
4,952 |
3663,5 |
4158,6 |
9,5652 |
|
900 |
5,414 |
3854,8 |
4396,1 |
9,7767 |
|
1000 |
5,875 |
4052,8 |
4640,3 |
9,9764 |
|
1100 |
6,337 |
4257,3 |
4891,0 |
10,1659 |
|
1200 |
6,799 |
4467,7 |
5147,6 |
10,3463 |
|
1300 |
7,260 |
4683,5 |
5409,5 |
10,5183 |
P = 2 BAR
|
T(ºC) |
v (m3/kg) |
u (kJ/kg) |
h (kJ/kg) |
s (kJ/kg × K) |
|
Sat. |
0,8857 |
2529,5 |
2706,7 |
7,1272 |
|
150 |
0,9596 |
2576,9 |
2768,8 |
7,2795 |
|
200 |
1,0803 |
2654,4 |
2870,5 |
7,5066 |
|
250 |
1,1988 |
2731,2 |
2971,0 |
7,7086 |
|
300 |
1,3162 |
2808,6 |
3071,8 |
7,8926 |
|
400 |
1,5493 |
2966,7 |
3276,6 |
8,2218 |
|
500 |
1,7814 |
3130,8 |
3487,1 |
8,5133 |
|
600 |
2,0130 |
3301,4 |
3704,0 |
8,7770 |
|
700 |
2,2440 |
3478,8 |
3927,6 |
9,0194 |
|
800 |
2,4750 |
3663,1 |
4158,2 |
9,2449 |
|
900 |
2,7060 |
3854,5 |
4395,8 |
9,4566 |
|
1000 |
2,9370 |
4052,5 |
4640,0 |
9,6563 |
|
1100 |
3,1680 |
4257,0 |
4890,7 |
9,8458 |
|
1200 |
3,3990 |
4467,5 |
5147,3 |
10,0262 |
|
1300 |
3,6300 |
4683,2 |
5409,3 |
10,1982 |
Per tabelle più dettagliate consultare il testo "Steam Tables" - Keenan, Hill, Keyes, Moore - New York - Ed.Wiley - 1969.