L'esempio che andremo ad analizzare ora non è altro che la generalizzazione dell'esercizio sullo scatolone adiabatico visto nella lezione scorsa. Cioè consideriamo inizialmente un contenitore chiuso, rigido, isolato e diviso in due parti da un setto isolante dove nei due scomparti, denominati 1 e 2, sono contenuti rispettivamente ossigeno e azoto. Ad un certo punto viene tolto il setto isolante, i due gas si miscelano, ed il sistema dopo poco tempo si porta ad uno stato finale in cui si è formata una miscela di ossigeno - azoto.

Calcolare :

1. le coordinate termodinamiche (p₃,T₃,V₃) nello stato finale del sistema note quelle iniziali.
2. la variazione di entropia del sistema alla fine del processo.

• Pressione del 1° scomparto : p₁ = 1 BAR
• Pressione del 2° scomparto: p₂ = 2 BAR
• Volume 1° scomparto: V₁ = 1 m³
• Volume 2° scomparto: V₂ = 2 m³
• Temperatura nel 1° scomparto: T₁ = 100 °C
• Temperatura del 2° scomparto: T₂ = 200 °C

Come primo passo possiamo calcolare il volume finale V₃ che è dato dalla somma dei volumi dei due scomparti visto che il nostro scatolone è rigido e quindi non subisce nessuna variazione di volume.

Quindi V₃ = V₁ + V₂ = 1 + 2 = 3 m³

 A questo punto abbiamo due incognite da determinare e quindi dobbiamo trovare due equazioni indipendenti. La prima è quella della conservazione delle masse cioè : M₃ = M₁ + M₂ . Utilizzando l'equazione dei gas perfetti ricaviamo le masse M₁ e M₂ relative ai due scomparti .

In particolare:

1) 2)

Ricordando che la costante di un gas è:

dove

ed m vale: per l'ossigeno e per l'azoto

otteniamo:

Convertiamo i valori di pressione e temperatura nel S.I. e cioè:

 ed andiamo a sostituire i valori numerici alle equazioni 1 e 2:

La seconda equazione la otteniamo utilizzando il primo principio della termodinamica ed osservando che il nostro scatolone è isolato ( non scambia calore con l'esterno Q=0 ) e rigido ( non compie lavoro L=0 ). Quindi l'energia interna del sistema nello stato iniziale è uguale a quella nello stato finale cioè: U_iniziale = U₃ dove l'energia interna nella stato iniziale è data dalla somma delle 2 energie interne U₁ e U₂ dei 2 gas presenti nello scatolone prima della miscelazione.

Il tutto si riassume scrivendo l'uguaglianza:

  3)

Prendendo sulle tabelle dei gas perfetti i valori del calore specifico a volume costante dei due gas abbiamo:

per l'ossigeno e per l'azoto

mentre il calore specifico a volume costante della miscela finale è :

Dall'equazione 3) ricaviamo la temperatura finale:

Per calcolare la pressione finale p₃ utilizziamo l'eq. di stato : p_3× V₃= M_3× R_3× T₃

dove la costante dei gas relativa alla miscela finale è :

Per cui l'ultima incognita da calcolare è :

Possiamo notare come la costante dei gas relativa alla miscela finale sia molto simile a quella dell'aria (287 J / kg K ). Questo ci fa supporre che i dati del problema abbiano portato alla formazione di una miscela perfettamente respirabile infatti l'aria è costituita per il 79% da azoto e 21% da ossigeno. Per approfondire ulteriormente ciò calcoliamo le percentuali di ossigeno e azoto:

Definiamo la massa percentuale di una sostanza o frazione ponderale come:

che nel nostro caso vale:

; ;

La massa percentuale viene adoperata solitamente dagli ingegneri mentre i chimici preferiscono usare le frazioni molari definite come:

ed otteniamo per i due gas:

;

;

Modifichiamo i dati del problema in modo tale da avere un caso particolare che successivamente andremo ad analizzare.

• Pressione del 1° scomparto : p₁ = 1 BAR
• Pressione del 2° scomparto: p₂ = 1 BAR
• Volume 1° scomparto: V₁ = 1 m³
• Volume 2° scomparto: V₂ = 2 m³
• Temperatura nel 1° scomparto: T₁ = 100 °C
• Temperatura del 2° scomparto: T₂ = 100 °C

Per come sono stati impostati i dati del problema verrebbe subito da dire: i due scomparti inizialmente sono alla stessa pressione e temperatura e una volta tolta la barra isolante il sistema viene a trovarsi alla stessa pressione e temperatura di partenza, inoltre non si è scambia calore e non è avvenuto lavoro per cui apparentemente con c'è stata nessuna trasformazione termodinamica….ERRORE!! La perdita di separazione dei due gas e la conseguente formazione di una miscela portano il sistema ad un aumento entropico.

 Per dimostrare ciò utilizziamo il principio di Dalton secondo il quale: ciascun gas non sente la presenza degli altri e si comporta come se ci fosse solo lui nel recipiente.

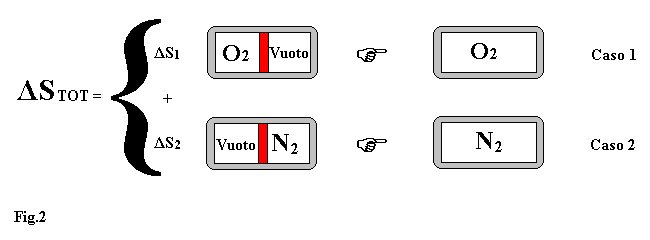
Come illustrato in fig.2 calcoliamo la variazione di entropia del sistema come somma delle variazioni di entropia di due processi elementari (caso1 e caso2).

Per le ipotesi fatte si può osservare che l'espansione di un gas nel vuoto non fa cambiare la sua temperatura. Infatti applicando il primo principio della termodinamica al caso1 abbiamo : U_1,FIN=U_1,INIZ= M₁ × C_v1 × T₁ ed essendo massa e calore specifico dell'ossigeno costanti segue che : T_1,FIN=T_1,INIZ , ragionamento analogo per l'azoto.

Quella che varia è invece la pressione ( nel vuoto la si è supposta uguale a zero ) infatti dall'equazione di stato: p × v = R × T otteniamo (essendo R e T costanti )

per il caso1:

  e la pressione finale è

mentre per il caso2:

  e la pressione finale è

 Calcoliamo le masse di ossigeno e azoto contenute nei due sottosistemi come abbiamo fatto nel punto a) :

ed andiamo a sostituire i nuovi valori numerici :

A questo punto non ci resta che calcolare le variazioni di entropia dei due sottosistemi per poi sommarle.

La variazione di entropia nel caso1 vale:

;

e nel caso2:

 Per cui l'aumento entropico del nostro sistema è :

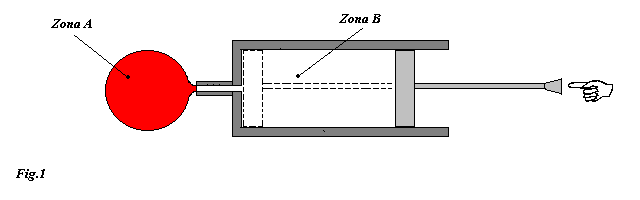
In questo esercizio consideriamo la classica pompa da bicicletta alla cui estremità è attaccato un contenitore a volume costante (vedi fig3 ).

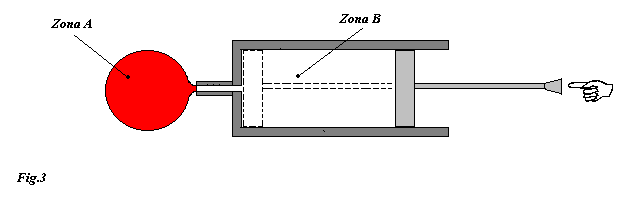
Inizialmente nella pompa vi è un certo quantitativo d'aria e ad un certo istante viene applicata una forza sullo stantuffo in modo da spingere tutta l'aria nel contenitore.

Note le pressioni e volumi nelle due zone (zona A e zona B) e la temperatura dell'aria nella pompa, calcolare il lavoro netto fatto per spostare nel contenitore tutta l'aria presente nella pompa. Supporre che il processo di compressione sia così rapido da non permettere al sistema di scambiare calore con l'esterno.

• Pressione iniziale nella zona A : p₀ = 1 BAR
• Pressione iniziale nella zona B : p₁ = 1 BAR
• Volume zona A: V₀ = 1 m³
• Volume iniziale zona B: V₁ = 2 m³
• Temperatura iniziale nella zona B: T₁ = 20 °C

 Prima della compressione il volume totale del nostro sistema (pompa + contenitore) vale : V_iniz = V₀+V₁= 1 + 2 = 3 m³ , mentre dopo la compressione lo stantuffo è arrivato al fondo della pompa per cui il volume finale vale:

Consideriamo il nostro sistema chiuso , per cui la massa presente prima e dopo la compressione rimane inalterata e quindi utilizzando l'equazione dei gas perfetti:

;

e ricordando che la costante di un gas è:

dove ; e la massa molare: per l'aria

ed e la temperatura T₁ = 293°K

possiamo calcolare la massa totale d'aria :

Essendo il processo di compressione della pompa molto rapido abbiamo che la trasformazione è adiabatica quindi non vi è scambio di calore con l'esterno ( Q= 0).

In una trasformazione adiabatica reversibile si ha che pressione e volume sono legati dalla relazione p× Vg = cost dove l'esponente vale:

.

Per calcolare il lavoro netto mi occorre la pressione finale del sistema che posso determinare sfruttando la precedente relazione delle trasformazioni reversibili cioè:

da cui ricavo la pressione finale :

;

A questo punto ho tutti i dati per calcolare il lavoro netto. Infatti utilizzando il secondo principio della termodinamica: U₂ - U₁ = Q - L ( dove Q = 0 essendo la trasformazione adiabatica ) otteniamo che il lavoro complessivo svolto sul sistema è :

-L= U₂ - U₁ ;

La curva che rappresenta la trasformazione che stiamo analizzando è rappresentata sul seguente diagramma p × V:

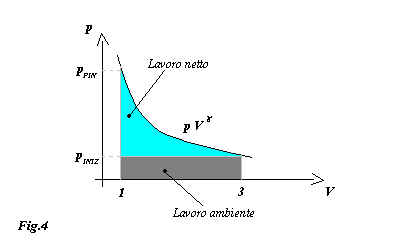
Il lavoro complessivo è quantificabile come l'area sottesa dalla curva 1-2 che a sua volta si divide in due componenti:

• Lavoro netto: energia che si deve spendere per spingere tutta l'aria contenuta nella zona B verso la zona A.
• Lavoro ambiente: energia che ci fornisce gratuitamente l'ambiente esercitando sul sistema una pressione atmosferica di 1 BAR.

Da questa osservazione e utilizzando l'equazione di stato dei gas perfetti ricaviamo che il lavoro totale è

:

e sostituendo i valori numeri vale:

Calcoliamo il lavoro ambiente:

I segni dei due lavori sono negativi avendo supposto per convenzione negativi i lavori sul sistema e positivi quelli del sistema.

In definitiva il lavoro netto vale:

Consideriamo un recipiente come quello illustrato in fig.5, contenente aria, al quale vengono forniti 2000J di calore.

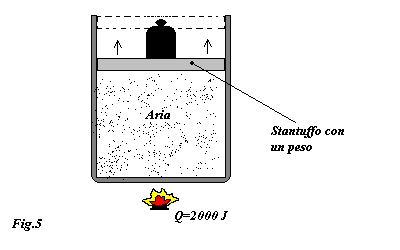
Si chiede di calcolare l'aumento di volume ipotizzando che la pressione interna al recipiente rimanga costante.

• Pressione interna al recipiente : p₁ = 1,1 BAR
• Pressione esterna al recipiente : p_atm = 1 BAR
• Volume iniziale del recipiente: V₁ = 0,50 m³
• Calore fornito: Q = 2000 J
• Temperatura iniziale dell'aria: T₁ = 20 °C

Come prima cosa trasformiamo le grandezze di partenza nel S.I. cioè:

La massa d'aria contenuta nel recipiente è data dall'equazione di stato dei gas perfetti: p× V = M × R × T e ricordando che la costante R=287 J/kg× K per l'aria

ricaviamo:

La massa d'aria rimarrà costante durante la trasformazione essendo il nostro sistema chiuso.

Supponiamo che il calore Q che forniamo al recipiente non si disperda nell'ambiente esterno ma vada tutto nel recipiente.

Per cui essendo Q = M × C_{p ×} ( T₂ - T₁ ) e il calore specifico dell'aria a pressione costante C_p=1,0035 KJ/kg× K possiamo ricavare la temperatura finale dell'aria all'interno del recipiente che vale:

Essendo la trasformazione a pressione costante ( p₂ = p₁ ) possiamo ricavare il volume finale attraverso l'eq. di stato dei gas perfetti applicata allo stato finale del sistema:

Come si può notare c'è stato un esiguo aumento di volume questo perché si è fornito al recipiente una quantità di calore molto bassa rispetto alla massa d'aria da riscaldare.

Riprendendo il sistema dell'esercizio 2 e supponendo di comprimere la pompa attraverso due tipi di trasformazioni, una isoterma ( T = costante ) e una adiabatica( Q=0 ).

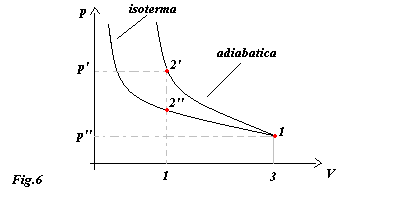
Determinare la miglior trasformazione, in termini di lavoro speso, per comprimere la pompa e portare quindi il sistema dallo stato iniziale 1 a quello finale 2’ o 2’’ a seconda della trasformazione.

• Pressione iniziale nella zona A : p₀ = 1 BAR
• Pressione iniziale nella zona B : p₁ = 1 BAR
• Volume zona A: V₀ = 1 m³
• Volume iniziale zona B: V₁ = 2 m³
• Temperatura iniziale nella zona B: T₁ = 20 °C

 Riportiamo qui di seguito i valori più significativi ottenuti nell'esercizio 2 e validi per entrambe le trasformazioni.

• Massa d'aria: M = 3,57 kg
• Costante caratteristica dell'aria R = 287 J / kg× K
• Volume iniziale del sistema: V_INIZ = 3 m³
• Volume finale del sistema: V_FIN = 3 m³

 Calcoliamo il lavoro totale che bisogna fare per portare il sistema da 1 a 2’’ attraverso una trasformazione isoterma.

Se il gas viene compresso alla temperatura costante di T = 293°K , ad esempio la pompa è immersa in un bagno termico a temperatura ambiente, vale la relazione tra p e V descritta dalla legge dei gas ideali : p× V = costante

e dalla relazione:

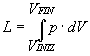
e usando l'equazione di stato: p× V = M× R× T

otteniamo il lavoro totale:

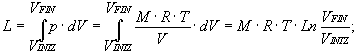
e andando a sostituire i valori:

Ricordando che nell'esercizio 2 la trasformazione adiabatica richiedeva un lavoro totale di : -424800 J possiamo dedurre confrontando i due risultati ottenuti che la miglio trasformazione è quella a temperatura costante.

Come si può notare abbiamo confrontato i lavori totali e non quelli netti. Questo perché in entrambi le trasformazioni il contributo energetico dell'ambiente è uguale e per l'esattezza vale L₀ = -200000J.

I lavori hanno segno negativo perché supposti per convenzione negativi quelli svolti sul sistema.