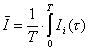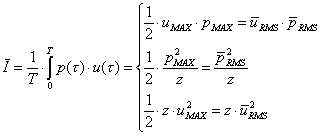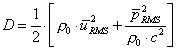Argomenti della lezione:

· Onde Piane Progressive

· Intensità acustica

· Coefficiente d’Assorbimento

· Densità Energia Sonora

Onde Piane Progressive:

Come è noto la propagazione del suono è possibile solo se c’è un mezzo elastico (solido, liquido o gas) in cui diffondersi, un particolare tipo d’onda sonora è un’onda piana progressiva nella quale tutte le particelle di un piano dello spazio si muovono in un'unica direzione con uguale velocità e pressione.

Una tipica sorgente è pistone che si muove all’interno di un tubo di lunghezza indefinita (quindi il moto è in una sola direzione):

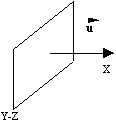
Esempio d’Onda Piana Progressiva (piano Y-Z)
che si muove lungo l’asse X con velocità u.

Si formulano le seguenti ipotesi:

1. Le particelle che costituiscono il mezzo ricevono l’energia da questo pistone che si muove e conservano lo stesso tipo di moto.

2. La legge che governa il moto del pistone, è di tipo sinusoidale; di conseguenza sinusoidale sarà il tipo di oscillazione locale.

Per calcolare la velocità delle particelle del piano e la pressione che generano localmente nel mezzo di propagazione è necessario utilizzare le equazioni di D’Alambert:

	(1)
	(2)
	(3)

Dove:

· F è il potenziale della velocità delle particelle del mezzo

· c è la velocità di propagazione del suono

· r₀ è la densità del mezzo

· p(x, y, z, t) è la funzione che esprime la pressione locale nello spazio e nel tempo.

· u(x, y, z, t) è la funzione che esprime la velocità locale delle particelle nello spazio e nel tempo.

Per le proprietà del moto e della pressione segue che la soluzione all’equazione di D’Alambert per un’onda piana progressiva è del tipo:

(4)

dove k è detto numero d’onda, e vale:

(5)

Usando la notazione di Eulero, la rappresentazione della precedente formula si può esprimere così:

(6)

Generalmente non si scrive Re perché solo la parte reale della formula è coerente in un contesto fisico.

Si nota che il sistema è lineare e quindi si comporta uniformemente con le onde introdotte e non ne altera il loro moto di tipo armonico. Contrariamente, in un sistema non lineare, oltre al segnale originale si sarebbero ottenuti dei segnali con andamento sempre oscillatorio ed armonico, ma con velocità (frequenza) di oscillazione maggiore e multipla di quella originale.

Il campo acustico è “perfettamente” lineare, cioè non altera di per se in nessun modo le onde sonore che lo attraversano.

Talvolta nelle applicazioni pratiche la non linearità può essere un difetto, come ad esempio nei trasduttori elettrici che non riescono a generare fedelmente (con linearità) i segnali che gli arrivano in ingresso. Ad esempio in un altoparlante la non linearità del trasduttore che lo compone non permette di riprodurre fedelmente le onde sonore così come erano in origine.

In certi casi la non linearità può essere una caratteristica ricercata e di pregio, come ad esempio negli strumenti a corda (violini, chitarre, ecc) che sono così in grado di produrre suoni complessi e molto armonici.

Sostituendo (4) in (2) e in (3) è possibile ricavare le espressioni di velocità delle particelle del mezzo e la pressione locale generata.

In particolare avendo limitato il moto ad una sola direzione nello spazio (nel nostro caso lungo l’asse X) l’operazione di gradiente si riduce ad una normale derivata direzionale su X.

Si calcola allora la velocità:

(7)

Mentre la pressione è:

(8)

In particolare si nota che le due funzioni ottenute sono sfasate di p/2 dato che quella originale è cosinusoidale, mentre le due trovate come soluzione hanno andamento sinusoidale.

Ricordando la definizione di impedenza caratteristica del mezzo:

(9)

e la definizione (5) si può ricavare l’impedenza per l’onda piana progressiva:

(10)

e ha valore reale.

Partendo dall’equazione (7), il valore della costante F_MAX si può ricavare ricorrendo al fatto che per x = 0 la velocità sia massima (u = u_MAX):

(11)

Da questo risultato, ricordando l’espressione (8) e dal fatto che:

è possibile ricavare il valore massimo della pressione (p_MAX) ed evidenziare la sua relazione con la velocità massima (u_MAX):

(11)

Ad esempio dati i valori:

si ottiene che il valore dell’impedenza è:

Se la pressione ad esempio è 1 Pa (P = 1 Pa) allora la velocità u è:

(1 Pa = 94 db circa)

Intensità acustica:

Il valore dell’Intensità Acustica (detta anche Intensità Media) si ricava facendo una media temporale dell’Intensità Istantanea:

(12)

Ricordando che:

è il valore dell’Intensità Istantanea e dato che si tratta di grandezze sinusoidali al posto delle grandezze massime di velocità e pressione si possono considerare i corrispettivi valori RMS:

(13) (14)

ricordando infine la definizione (10) si può calcolare il valore dell’integrale appena visto:

(15) (16) (17)

Le tre espressioni ricavate (15), (16) e (17) sono equivalenti tra loro, però occorre prestare attenzione nell’utilizzarle; infatti, solo nel caso delle onde piane progressive c’è proporzionalità tra pressione (o velocità) e intensità media, normalmente si deve considerare che l’impedenza z non è reale, ma è complessa e quindi dotata di un certo sfasamento con un diverso risultato delle espressioni (15), (16) e (17), l’integrale (12) invece ha valenza generale.

Questo fatto è stato scoperto e preso seriamente in considerazione solo verso la fine degli anni ’80, prima di allora si considerava che la proporzionalità valesse in ogni caso e tali espressioni erano comunemente usate per calcolare l’intensità.

Considerando quindi il caso più generico in cui l’impedenza z è complessa e prendendo come riferimento il vettore velocità u che per completezza si riporta qui:

si calcola la nuova espressione della pressione:

(18)

che contiene quindi lo sfasamento j.

Il valore complesso dell’impedenza che si ricava dalle due espressioni è:

(19)

Coefficiente d’Assorbimento:

In condizioni normali un’onda piana si propaga nel mezzo (ad esempio nell’aria) indefinitivamente fino ad esaurire la sua energia, se non incontra ostacoli durante il suo tragitto.

Si considera un sistema costituito da un tubo di lunghezza non definita e chiuso da un’estremità con un tappo costituito da un materiale con particolari caratteristiche meccaniche che sono diverse da quelle dell’aria.

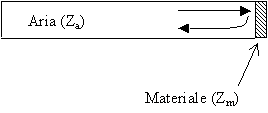
L’impedenza del materiale si suppone essere Z_m (reale) ed è tale che la velocità u in quel punto è nulla.

Quando l’onda originale incontra il materiale è riflessa e quindi torna indietro andando a sovrapporsi alle onde che viaggiano da sinistra verso destra, causando uno sfasamento nel moto ondulatorio che interferisce con il suo corretto propagarsi alterandone le caratteristiche.

Se l’onda è riflessa completamente lo sfasamento tra i due treni d’onde opposte è di p/2 e il risultato del loro “scontrarsi” in questo caso particolare è il loro annullamento: si annullano a vicenda.

Analizzando più in dettaglio il fenomeno si ha che quando il treno d’onde iniziale viene a contatto con un materiale con caratteristiche meccaniche (principalmente impedenza) diverse dal mezzo di propagazione (nel caso di prima il materiale con impedenza Z_m che è diversa da quella Z_a dell’aria) si suddivide in due parti: una parte delle onde è riflessa dal materiale e torna indietro, l’altra parte è assorbita dal materiale stesso.

In termini di intensità si definiscono tre indici:

· Intensità Incidente (I_i) : è l’intensità che ha l’onda appena prima di entrare in contatto con il materiale;

· Intensità Assorbita (I_a) : è l’intensità della parte d’onda assorbita;

· Intensità Riflessa (I_r) : è l’intensità della parte d’onda riflessa;

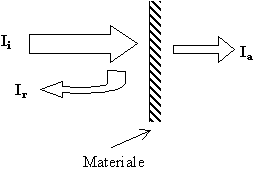
Esprimendo quanto detto in formule:

(20)

dividendo la precedente per I_i si ha

(21)

dove si individuano due nuovi valori:

· Coefficiente d’Assorbimento: = a

· Coefficiente di Riflessione: = r

e la loro somma da 1; in particolare si possono vedere così:

(22)

In realtà oltre all’indice di assorbimento del materiale è necessario considerare l’indice di trasmissione (I_t) del suono ad un ambiente adiacente e a contatto con il materiale stesso.

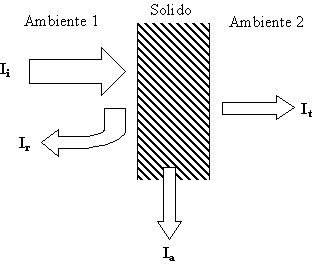
Esprimendo questi concetti più formalmente si ottiene:

(23)

dividendo la precedente per I_i si ha

(24)

dove si individua un nuovo valore:

· Coefficiente di Trasmissione: = t

la somma dei tre coefficienti finora individuati da sempre 1.

Usando i nuovi valori trovati a, r e t si può esprimere la (23) così:

(25)

in particolare ora si è in grado di individuare il Coefficiente di Assorbimento Acustico Apparente (a), che è il principale strumento per valutare la capacità di assorbimento acustico di un materiale; il suo valore è:

(26)

Come si vede dalla definizione di Coefficiente Apparente, per valutare la capacità di assorbimento di un materiale non importa la quantità di suono assorbito o trasmesso ad un ambiente esterno collegato, ma la quantità di onde riflesse; è anche per questo che tale coefficiente è detto di assorbimento apparente, in realtà infatti considera solo le onde riflesse e la condizione migliore si ha quando tutto il suono è assorbito dal materiale.

Il caso migliore ed ideale si ha quando r = 0 e quindi a = 1, in questo caso si parla di materiali perfettamente fonoassorbenti, nel caso (a = 0 e r = 1) si parla invece di materiali perfettamente riflettenti.

Facendo un esempio pratico, considerando la diffusione del suono in una stanza chiusa con delle finestre, il migliore materiale assorbente acusticamente sono le finestre aperte; infatti l’aria è il materiale con minor coefficiente di riflessione acustica essendo la sua densità e consistenza molto piccola (ovvero offrendo un impedenza molto piccola).

Altri buoni materiali che offrono alto assorbimento delle onde sonore sono i materiali espansi a celle aperte come il poliuretano espanso, lana di roccia, velluto, ecc. o in generale i materiali detti fonoassorbenti (con valori di a prossimi a 1). La caratteristica comune di questi materiali è che si lasciano attraversare dall’aria opponendo però molta resistenza, il che equivale a presentare un’alta impedenza per le onde sonore. Il principio con cui funzionano tali materiali fonoassorbenti è quello di incanalare le onde sonore in tanti cunicoli di piccolissime dimensioni smorzando le onde sonore per effetto del loro attrito contro le pareti di tali cunicoli.

In generale il grado di assorbimento varia in funzione della frequenza (f) e dello spessore del materiale (confrontando lo stesso materiale a diversi spessori).

Graficamente:

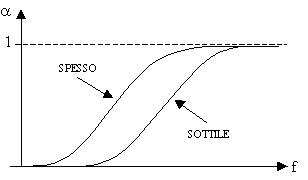
La capacità fonoassorbente di un materiale quindi non è costante a tutte le frequenze e per essere apprezzabile deve essere dell’ordine della lunghezza delle onde sonore che deve smorzare. Inoltre ci sono comportamenti limite: alle basse frequenze per ottenere alti valori di a è necessario usare materiali con grandi spessori o meglio ricorrere ad altre tecniche di assorbimento acustico; al contrario alle altissime frequenze bastano materiali semplici e di piccolo spessore.

Come si vede è difficile individuare un corretto spessore in grado di comportarsi uniformemente a tutte le frequenze; una regola che comunque è usata per stabilire quanto spesso deve essere il materiale fonoassorbente è:

(27)

(dove s lo spessore del materiale da usare e l la lunghezza d’onda del suono).

Per assorbire le basse frequenze di solito si usano sistemi di doppie pareti una esterna cedevole al suono e una interna rigida, separate da un sottile strato d’aria o di materiale elastico.

L’effetto che si crea è simile a quello di una massa M collegata ad una molla fissata (di elasticità k) ad una parete come in figura:

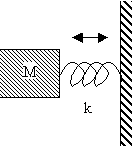
Questo sistema quando si trova in condizioni di risonanza assorbe completamente le oscillazioni imposte dalle onde sonore. Tale frequenza di oscillazione, detta frequenza naturale di oscillazione è:

(28)

E’ comunque importante notare la distinzione tra assorbimento acustico ed isolamento acustico: nel primo caso si fa riferimento alla riflessione delle onde sonore, nel secondo caso si parla di isolamento di un ambiente dalle onde acustiche di un’altro ambiente ad esso collegato.

Densità Energetica Sonora:

La propagazione di un’onda in un mezzo qualsiasi comporta anche la propagazione di energia data dalla presenza di variazione di velocità e pressione a livello locale. Per misurare tale energia si introduce il coefficiente di Densità di Energia (D) e vale:

(29)

Come si vede tale coefficiente misura l’energia per unità di volume (metro cubo).

Prendendo come riferimento un’onda piana di area pari ad 1 m² che in un secondo percorre c m (dove c è la velocità del suono) si osserva che l’intensità I dell’onda si “diluisce” all’interno del parallelepipedo di volume c m³.

Graficamente:

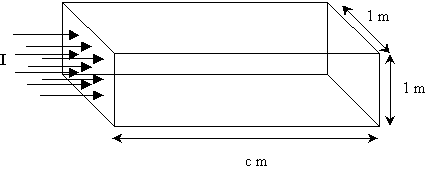
Da quest’osservazione si ricava la definizione del coefficiente D :

(30)

La densità D si può scomporre in due componenti: oscillante (tipica delle oscillazioni locali) e propagante (tipico delle onde piane progressive):

(31)

Come visto in precedenza l’intensità si può scomporre in diverse sottocomponenti, in particolare considerando solo l’intensità istantanea (I_i) e quella riflessa (I_r) si ha:

(32)

Nel caso delle onde piane progressive D è così composto:

(33)

e confrontando con (32) si ricavano i seguenti coefficienti di densità:

(34) (35)

che sono:

· D_r = Densità riflessa

· D_i = Densità istantanea

A questo punto si può riscrivere il coefficiente di densità D così:

(34) (35)

Conoscendo (32) e (35) si possono ricavare i coefficienti I_i e I_r in funzione dei due soli parametri D e I che possono essere facilmente rilevati con appositi strumenti di misurazione:

(36) (37)

A questo punto è possibile ricavare il valore del coefficiente di assorbimento apparente (a) sempre in funzione di D e I. Come si è visto in precedenza vale:

e dalla (36) e (37) segue facilmente:

(38)

Generalmente l’energia si può scomporre in cinetica e potenziale, ricordando che per un onda piana progressiva energia cinetica (legata alla velocità) e potenziale (legata alla pressione) hanno valore equivalente dato che si ricavano dallo stesso integrale, si possono introdurre due nuovi definizioni di densità: Densità Cinetica (D_c) e Densità Potenziale (D_p).

Le espressioni di energia cinetica (I_c) e potenziale (I_p) sono:

(39) (40)

Di conseguenza i valori energetici in cui si scompone la densità “totale” sono:

(41) (42)

Infatti anche in questo caso vale la legge della conservazione dell’energia, quindi l’energia cinetica si trasformerà in potenziale e viceversa, anche se normalmente l’energia potenziale è quella che prevale, ma in totale è sempre la stessa e vale:

(43)

Questa è la formula usata normalmente nelle misurazioni di densità.

Riassumendo per conoscere le caratteristiche del sistema da analizzare:

· Dal punto di vista fisico è necessario rilevare i valori di velocità e pressione.

· Dal punto di vista energetico è necessario rilevare i valori di intensità e densità.

Solo recentemente (intorno al ’95) l’ISO ha emanato delle norme che caratterizzassero meglio la distinzione tra caratteristiche fisiche ed energetiche nel campo sonoro. Fino a non molto tempo fa infatti si tendeva a utilizzare indifferentemente e spesso congiuntamente le caratteristiche energetiche e fisiche delle onde sonore, ma come detto precedentemente questo vale solo per le onde piane progressive (negli altri casi infatti l’espressione (43) non vale, infatti si fa riferimento a grandezze energetiche quali la densità come derivate direttamente da grandezze fisiche e vettoriali).