Fluidodinamica
Argomenti trattati:
·
Definizioni generali
·
Viscosità e aderenza
· Legge
di Newton
·
Viscosimetro a rotazione
· Tipi
di fluidi
·
Esperimento e N° di Reynolds
· Teoria
dei modelli
·
Parabola di Poiseuille
Definizioni generali
Un liquido può scorrere sia dentro che fuori ad un determinato corpo:nel primo caso si parla di MOTO INTERNO, nel secondo caso di MOTO ESTERNO.
1) Nel moto interno calcoliamo le cadute di pressione che avvengono tra due sezioni del corpo attraversato dal fluido: tali perdite sono chiamate PERDITE DI CARICO .La scienza che si occupa di ciò è l’idraulica e studia in particolare il moto dei fluidi incomprimibili (il fluido, oltre che liquido può essere anche gassoso,in quanto considero la densità costante).
2) Nel moto esterno calcoliamo invece la risultante delle forze che viene prodotta dall’interazione fluido-struttura: che sia il fluido a muoversi ed il corpo fermo o viceversa non ha importanza in quanto considero il moto relativo tra un corpo solido ed un fluido (es. missile,automobile,vento che investe un edificio).Ci interessa dunque ricavare la cosiddetta FORZA DI TRASCINAMENTO.
Le equazioni che governano questi problemi sono sostanzialmente le stesse,anche se chiaramente applicandole alle due diverse situazioni porteranno a risultati leggermente diversi.
Viscosità e aderenza
La VISCOSITA’ è l’insieme delle forze tangenziali tra superficie e fluido e
tra strati di fluido diversi che si oppone al moto del fluido stesso rispetto
alla superficie.Queste forze tangenziali sono dette TENSIONI (t) e hanno la forma del tipo:
![]()
![]() (1)
(1)
dove
F è la forza che agisce su un
elemento di area A che si oppone al
verso del movimento del liquido.
Prendiamo un fluido in moto relativo rispetto ad una superficie solida:se
tracciamo in un dato istante un segmento colorato normale alla superficie,e se
dopo un intervallo di tempo si fotografa ancora la porzione di liquido
considerato,si nota che in breve tempo tale segmento si è deformato nel senso
del moto,dando luogo ad una curva che rappresenta la variazione della velocità
del fluido al variare della distanza dalla superficie solida in quiete
(fig.1).La particella colorata a contatto con la superficie solida non si è
spostata,ha avuto cioè velocità nulla,verificando così il fenomeno dell’ADERENZA.
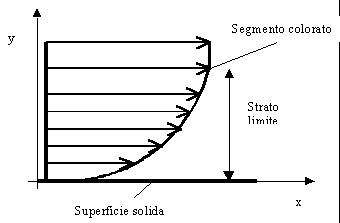
Fig.1: profilo di velocità di un fluido e strato limite
La porzione di fluido all’interno del quale il fluido subisce la variazione di velocità,è detta STRATO LIMITE.
Un fluido che investe un
determinato corpo non solo produce tensioni tangenziali (t) dovute alla viscosità, ma anche forze normali dovute alla pressione (p) prodotte dalle particelle del fluido (fig.2).
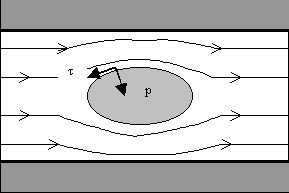
Fig.2: forze tangenziali e
normali agenti sul corpo per effetto del movimento del fluido
Legge di Newton
Tale legge sancisce la
proporzionalità lineare tra la tensione tangenziale t e la derivata parziale della velocità u
del fluido rispetto ad y tramite la
viscosità m:
![]() (2)
(2)
t : tensione che si esercita nella direzione (x)
sulla superficie normale ad (y) rivolta verso le (y) decrescenti (è opposta al
verso del moto e quindi ho il segno – nella formula).
u : è la velocità
m : costante di viscosità propria di ogni fluido,è
un numero puro e si misura in
![]()
La (2) fu enunciata con la specificazione y=0, descrivendo così la forza
reciproca tra parete solida e fluido in moto;il fluido “tira” la parete verso
destra con uno sforzo t e la parete frena il fluido con uno sforzo uguale
e contrario (fig.3). Tuttavia la legge vale anche se non ho la parete solida in
quanto all’interno di un fluido,lo strato che scorre ad una velocità superiore
di quella dello strato confinante esercita una forza di trascinamento sullo
strato più lento e quest’ultimo esercita una forza uguale e contraria di
frenaggio sullo strato più veloce,continuando così a valere il bilancio delle
forze.
![]()
![]()
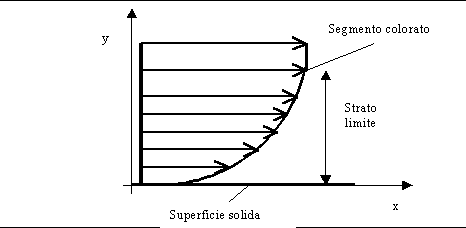
Fig.3:forza di trascinamento(verso destra) e forza di frenaggio(verso sinistra) tra fluido ed acqua.
Oltre a m, chiamata
VISCOSITA’ DINAMICA, esiste anche la VISCOSITA’ CINEMATICA n, definita come:
![]()
![]() (3)
(3)
dove r è la densità del fluido.
Dalle unità di misura si nota che m è una tensione mentre n no; non bisogna confonderle in quanto solo nel
caso dell’acqua esse sono circa uguali ( r dell’acqua è 1) mentre in tutti gli altri casi sono molto diverse!!!(vedere
le 2 tabelle alla fine della tesina).
Dunque secondo la legge di Newton, il comportamento di un fluido è
caratterizzabile dalla viscosità che non è costante, bensì varia al variare
della temperatura.Tale legge,come tutte le leggi,non è esatta,è solo
un’approssimazione della realtà,ed in particolare è valida solo per acqua ed
aria, mentre tutti gli altri fluidi deviano da questa legge.
Viscosimetro a rotazione
Lo strumento migliore per studiare la viscosità di un fluido è il
VISCOSIMETRO A ROTAZIONE. E’ costituito da un motorino elettrico, da cui esce
un piccolo albero, alla base del quale si trova un cilindretto chiamato ROTORE
o EQUIPAGGIO MOBILE. Il motorino imprime all’albero una rotazione di una certa
velocità angolare; immergo ora il cilindretto in una tazza cava di forma
cilindrica (fig.4). Tra i due cilindri,entrambi di acciaio inox, scorre del
liquido ( in genere acqua).Pongo in rotazione con velocità angolare costante w il cilindro esterno: con il passare del tempo,
notiamo dapprima mettersi in rotazione gli strati più esterni del fluido e
successivamente quelli via via più interni fino a che entra in rotazione anche
il cilindro interno.
Questo processo può intervenire soltanto se in seno al fluido nascono degli
sforzi diretti tangenzialmente al moto e quindi in grado di trascinare i
successivi strati di fluido ed anche il cilindro interno,trasmettendo la coppia
applicata al cilindro esterno per mantenerlo in rotazione.
Se voglio mantenere in quiete il cilindro interno,occorre applicarvi una
coppia resistente a mezzo,per esempio,di una forza tangenziale t. Notiamo allora che la velocità del fluido alla
parete del cilindro esterno è wr![]() , mentre è nulla alla parete del cilindro
interno;questo indica che alle pareti il fluido si muove con la stessa velocità
di queste e cioè non esiste slittamento tra pareti e fluido.Consideriamo ora un
generico cilindro di raggio r (
, mentre è nulla alla parete del cilindro
interno;questo indica che alle pareti il fluido si muove con la stessa velocità
di queste e cioè non esiste slittamento tra pareti e fluido.Consideriamo ora un
generico cilindro di raggio r (![]() <
< ![]() ):il fluido che si trova all’esterno di questa superficie per
poter far muovere quello posto all’interno,deve esercitare sulla superficie stessa un’azione di
trascinamento risultante da sforzi diretti, in ogni punto,tangenzialmente al
moto nello stesso verso della velocità;un’azione identica ma di verso opposto
viene esercitata dal fluido interno su quello esterno,che risulta perciò
frenato nel suo movimento.
):il fluido che si trova all’esterno di questa superficie per
poter far muovere quello posto all’interno,deve esercitare sulla superficie stessa un’azione di
trascinamento risultante da sforzi diretti, in ogni punto,tangenzialmente al
moto nello stesso verso della velocità;un’azione identica ma di verso opposto
viene esercitata dal fluido interno su quello esterno,che risulta perciò
frenato nel suo movimento.
Quando l’intercapedine tra i due cilindri è molto piccola rispetto ai loro
raggi, cosicché si possa ritenere che la velocità del fluido vari linearmente
fra le due pareti solide, le esperienze condotte nelle più svariate condizioni
( variando i raggi o la velocità angolare w ) mostrano che lo sforzo tangenziale t è direttamente proporzionale alla differenza di velocità ![]() e inversamente
proporzionale alla distanza
e inversamente
proporzionale alla distanza ![]() tra i due cilindri tramite la viscosità m:
tra i due cilindri tramite la viscosità m:
![]() (4)
(4)
Il motore è dotato di una cella di coppia che misura il momento M e la velocità angolare v.La prova che faccio consiste dunque nel far
variare progressivamente la velocità di rotazione all’interno della tazza
partendo da valori molto bassi e aumentandola mano a mano, misurando in
corrispondenza di ogni velocità il momento.Il momento è espresso come:
M=t s r![]() (5)
(5)
Dove t è la forza tangenziale, r![]() è il raggio del cilindretto interno ed s è la superficie laterale del
cilindro.
è il raggio del cilindretto interno ed s è la superficie laterale del
cilindro.
Dalla (2) e dalla (5) concludo quindi che c’è proporzionalità tra momento M e gradiente di velocità ![]() .
.
![]()
![]()
![]()
![]()
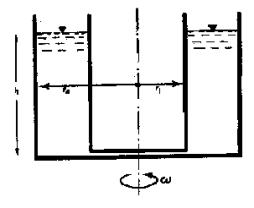
Fig.4:viscosimetro
a rotazione costituito dal cilindretto interno di raggio r![]() e da quello esterno di raggio r
e da quello esterno di raggio r![]() .
.
Tipi di fluidi
Per i gas e per la maggior parte e per la maggior parte dei liquidi a basso
peso molecolare, si ha che m dipende solo dalla natura del fluido e dal suo
stato fisico;tali fluidi ubbidiscono perfettamente alla legge di Newton e sono
quindi detti NEWTONIANI (es. acqua, benzina, butano) e sul grafico (fig.5)
hanno un andamento lineare, con una pendenza data da ![]() .
.
Esistono però molti fluidi che non seguono la legge di Newton in quanto m risulta legato ad altre grandezze caratteristiche
delle particolari condizioni sperimentali, oltre che al valore dello sforzo
tangenziale t![]() e al tempo.Per
quanto riguarda la dipendenza dal
valore dello sforzo, è possibile distinguere i fluidi NON NEWTONIANI in
PSEUDUPLASTICI e DILATANTI:
e al tempo.Per
quanto riguarda la dipendenza dal
valore dello sforzo, è possibile distinguere i fluidi NON NEWTONIANI in
PSEUDUPLASTICI e DILATANTI:
Pseudoplastici: tendono a smollarsi e il valore di m cala al crescere del gradiente di velocità ( es.
fanghi, gelatine, polimeri liquidi come gomma o acetato di cellulosa).
Dilatanti: tendono ad indurirsi e il valore di m aumenta al crescere del gradiente di velocità ( es. grassi, sabbia in
sospensione).
Una proprietà importante di questi fluidi è quella di avere memoria.Cioè
dopo che ho smollato uno pseudoplastico,ovvero dopo che ne ho rotto una serie di legami interni che
tenevano unite le particelle, esso tende a restare molle, avendo così memoria
del passato.Se dunque torno indietro, non appena cala la velocità di
deformazione, lo sforzo cala rapidamente e il fluido compie un cammino inverso
a quello che ha fatto prima, seguendo un andamento ISTERETICO.
Ovviamente accade l’opposto per il materiale dilatante, che dopo che si è
indurito tende a rimanere duro anche se riduco la velocità e segue anch’esso un
ciclo isteretico.
Spesso quindi i dilatanti sono anche fluidi REOPEPTICI, cioè fluidi che una
volta induriti, rimangono tali, presentando un aumento di m per effetto della lunga applicazione di uno
sforzo tangenziale costante ( a temperatura costante) (es. impasti di gesso in
acqua).Gli pseudoplastici invece, possono anche essere TIXOTROPICI, cioè fluidi
che una volta ammolliti tendono a rimanere tali e presentano una diminuzione di
m sempre per effetto dell’applicazione dello sforzo
tangenziale (es. prodotti alimentari, vernici).
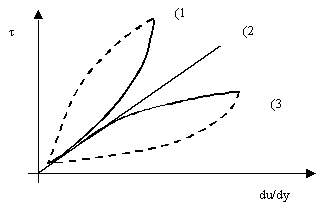
Fig.5:diagramma della viscosità dei fluidi 1)Dilatanti 2)Newtoniani 3)Pseudoplastici
Tale grafico prende il nome di CARATTERISTICA
REOLOGICA DI UN FLUIDO.
Esistono inoltre dei fluidi particolari chiamati
FLUIDI DI BINGHAM, che inizialmente si comportano da solidi e quindi fino ad un
certo sforzo iniziale t![]() non si deformano, poi, superato tale sforzo, iniziano
la deformazione (es. vetro, maionese, burro).
non si deformano, poi, superato tale sforzo, iniziano
la deformazione (es. vetro, maionese, burro).
Esperimento e N![]() di Reynolds
di Reynolds
L’esperimento condotto da Reynolds, consiste nel prendere un serbatoio
pieno d’acqua con un’apertura sulla parete: in tale apertura, è innestato un
tubo di materiale trasparente, lungo il quale scorrerà l’acqua fino all’uscita.
Ho inoltre un tubicino inserito nel serbatoio in corrispondenza del centro
del tubo.Variando l’altezza del pelo libero o il diametro del condotto, cambia
la velocità con cui il liquido scorre nel tubo.Studiamo dunque l’andamento del
liquido nel condotto al variare della sua velocità media w: per osservare meglio quanto accade, inietto con il tubicino del
liquido colorante nel condotto (Fig.6).
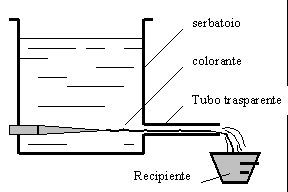
Fig.6: rappresentazione dell’esperimento di Reynolds
A questo punto si verificano due casi:
1) Quando l’acqua scorre a bassa velocità, il liquido
colorante, pur essendo libero di vagare per tutto il condotto, di fatto non lo
fa, e scorre dentro ad un ipotetico tubicino detto TUBO DI FLUSSO, rimanendo
così imperturbato per tutto l’asse del condotto (fig.7).Siamo dunque in
presenza di MOTO LAMINARE.
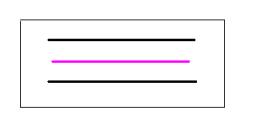
Fig.7: Moto laminare:il liquido colorato non è perturbato
2) Se aumento l’altezza del pelo libero, aumenta anche la velocità con cui il fluido scorre nel condotto, e scopro che al di sopra di una certa VELOCITA’ CRITICA , il liquido colorato inizia ad oscillare fino a mescolarsi del tutto con l’acqua (fig.8).Si verifica quindi il MOTO TURBOLENTO.
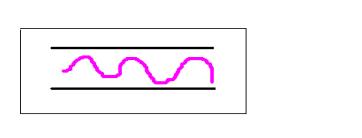
Fig.8: Moto
turbolento: il liquido colorato si mescola con l’acqua
Dal suo esperimento
Reynolds scoprì che la transizione dal regime di moto laminare a regime di moto
turbolento ( e viceversa) dipende sempre da 4 grandezze: velocità w,densità r e viscosità m del fluido e diametro D del condotto.Confrontando due a due queste grandezze vide dai
grafici che esse dovevano essere tutte
legate tra loro: tale legame è espresso dal NUMERO DI REYNOLDS Re:
Re =![]() (6 )
(6 )
In particolare, ![]()
![]()
![]() se Re<2100 siamo in presenza di moto laminare,
se invece Re>4000 abbiamo il moto turbolento. All’interno di questo
intervallo non è però possibile stabilire quale sarà il comportamento del
fluido.
se Re<2100 siamo in presenza di moto laminare,
se invece Re>4000 abbiamo il moto turbolento. All’interno di questo
intervallo non è però possibile stabilire quale sarà il comportamento del
fluido.
Teoria dei modelli
![]() Molto
spesso nella pratica non si conoscono la viscosità (reale o apparente), lo
sforzo iniziale e la dipendenza dalla temperatura di moltissimi fluidi.E’
proprio grazie alla teoria dei modelli che posso generalizzare i risultati che
si ottengono dagli esperimenti, riuscendo così a coprire una casistica molto
ampia senza dover fare un numero enorme di prove diverse ( applicazioni
importanti di tale teoria vengono fatte nell’aeronautica, nella missilistica e
nella Formula 1).
Molto
spesso nella pratica non si conoscono la viscosità (reale o apparente), lo
sforzo iniziale e la dipendenza dalla temperatura di moltissimi fluidi.E’
proprio grazie alla teoria dei modelli che posso generalizzare i risultati che
si ottengono dagli esperimenti, riuscendo così a coprire una casistica molto
ampia senza dover fare un numero enorme di prove diverse ( applicazioni
importanti di tale teoria vengono fatte nell’aeronautica, nella missilistica e
nella Formula 1).
Fu Reynolds ad inventare questa teoria, consentendoci di riportare sui modelli originali i risultati
ottenuti dalle esperienze fatte su modelli in scala (più piccoli di quelli
originali).
La teoria dei modelli si basa su due concetti fondamentali:
1)
Utilizzare equazioni
fisiche dimensionalmente omogenee.
2)Adimensionalizzazione, cioè si riscrivono le equazioni moltiplicando e dividendo per opportune grandezze in modo che l’equazione contenga tutti numeri puri e le grandezze siano anch’esse state adimensionalizzate.
Per adimensionalizzare una grandezza si fa il rapporto tra tale grandezza ed una grandezza di riferimento.
Se ad esempio prendo una lastrina di materiale solido investita da un
fluido con velocità u![]() ,noto dal profilo di velocità, che ad una certa distanza
dalla lastrina stessa la velocità rimane u
,noto dal profilo di velocità, che ad una certa distanza
dalla lastrina stessa la velocità rimane u![]() ,mentre all’avvicinarmi alla lastrina ho una progressiva
diminuzione della velocità (fig.9).
,mentre all’avvicinarmi alla lastrina ho una progressiva
diminuzione della velocità (fig.9).
Per ottenere dunque la velocità adimensionale u* devo fare il rapporto tra la
velocità u e la velocità di
riferimento u![]() .
.
u*=![]() (7)
(7)
Si nota dunque che i valori assunti da u* variano tra 0 (quando sono a
contatto con la superficie della lastrina) e 1 (quando sono alla massima
distanza dalla lastrina,cioè quando la velocità vale u![]() ).
).
![]()
![]()
![]()
![]()
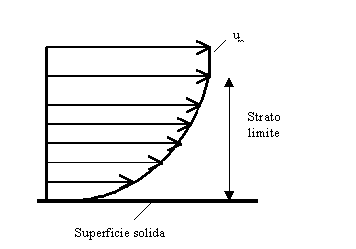
Fig.9: profilo di
velocità di un fluido a contatto con una lastrina solida
La teoria dei modelli, o ANALOGIA DI REYNOLDS, afferma che quando si hanno le equazioni in forma adimensionale, la soluzione di questa equazione è sempre la stessa.
Nel processo di adimensionalizzazione, è spesso usata la LUNGHEZZA CARATTERISTICA “ L” :tuttavia è spesso difficile scegliere la grandezza caratteristica adatta per adimensionalizzare le equazioni di un dato problema (es. per un tubo investito ortogonalmente da un fluido, la lunghezza caratteristica è il diametro del tubo stesso, mentre se il fluido investe il tubo scorrendo lungo di esso la lunghezza caratteristica è la lunghezza del tubo; per un’ala di un aereo invece consideriamo la corda alare).
Dunque grazie alla teoria dei modelli, mi basta per esempio fare 1000 esperimenti per trovare tutte le soluzioni possibili ( altrimenti avrei dovuto fare 1000 esperimenti per ciascuna delle 4 grandezze D,w,m,r per un totale di 1000 miliardi di prove!!) in quanto ho una sola variabile e non più 4.
Nella risoluzione di un
problema, il dato di ingresso è il N° di Reynolds, e secondo la teoria dei modelli, la
grandezza generica dimensionale A è espressa in funzione di altre 3 grandezze
dimensionali che sono: Re, x*, e*.
A=f (Re, x*, e* )![]() (8)
(8)
Definiamo ora la SCABREZZA RELATIVA e* come :
![]() (9)
(9)
e il POSIZIONATORE DELLA REGIONE D’INGRESSO x* come:
x*=![]() (10)
(10)
dove D è il diametro in mm del tubo in cui scorre
il liquido.
Nella (9) e è la SCABREZZA (o rugosità) del tubo, cioè l’altezza media in mm delle
asperità sulla superficie della parete.Tale fattore dipende dalla possibilità
che le pareti del tubo non siano lisce ma rugose.
Nella (10) x
è un parametro che indica la distanza
dal punto di imbocco del tubo.La dipendenza da questo termine è spesso
trascurata.Infatti le perdite di carico sono funzione di x solo nella regione d’ingresso del tubo, in quanto la velocità è
funzione di x; tale dipendenza
invece scompare nel regime sviluppato che, nel caso più frequente di regime
turbolento, si instaura dopo solo 10 diametri.
Il dato di uscita del problema è la PERDITA DI
CARICO, cioè la caduta di pressione tra due sezioni di un corpo.
Definiamo dunque il FATTORE DI ATTRITO x come:
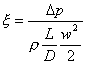 (11)
(11)
dove Dp è la caduta di pressione, L e D sono
rispettivamente la lunghezza e il diametro del tubo, r e w sono invece la densità e la velocità media del fluido.
x è un numero puro e può essere visto come il
rapporto tra due energie, cioè tra l’energia potenziale di pressione ![]() e l’energia
cinetica.
e l’energia
cinetica.
Formalmente il risultato del calcolo è:
x=f (Re, x*, e*) (12)
Tuttavia, in un tubo liscio a regime posso
trascurare x* e e*, ottenendo semplicemente:
x=f (Re) (13)
Siccome la funzione f normalmente non è nota, uso grafici e tabelle che mi riportano i
dati sperimentali e mi consentono di ricavare il legame tra Re e x.
Per calcolare le perdite di carico mi basterà
fare:
![]() (14)
(14)
Parabola di Poiseuille
Esiste un unico caso in cui posso ricavare la soluzione della (13) per via analitica, senza cioè l’uso di tabelle o grafici.
Prendo un fluido che imbocca un condotto provenendo da un grande
serbatoio:il profilo di velocità, inizialmente piatto, o quasi, si deforma via
via fino ad assumere la configurazione detta PARABOLA DI POISEUILLE, che
vedremo dopo in forma analitica.Nella fig.10 , sono evidenziati alcuni profili
di velocità in regione d’ingresso.Al rallentamento del fluido all’interno dello
strato limite,corrisponde un’accelerazione di quello che si trova fuori,dovendo
essere garantita la continuità di portata.Se la lunghezza del condotto è
sufficiente in relazione al suo diametro, i confini dello strato limite tendono
ad incontrarsi sull’asse del condotto:in teoria il contatto si ha solo
asintoticamente, ma in pratica a circa 20-30 diametri dall’imbocco si può
ritenere che il profilo abbia ormai raggiunto la sua configurazione definitiva,
che viene detta PROFILO COMPLETAMENTE SVILUPPATO, sia esso laminare o
turbolento.
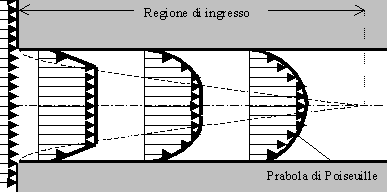
Fig.10: sviluppo dello strato limite dinamico
nella regione d’ingresso
Prendiamo dunque un tubo liscio a sezione
circolare con raggio R, in cui
scorre del liquido con velocità u e
consideriamo un elemento di volume di lunghezza L e raggio r, centrato
rispetto al piano di simmetria del condotto (Fig.11).
Poniamo le seguenti ipotesi:
·Sistemo stabilizzato
·Moto laminare
·Regime stazionario rispetto a spazio e tempo
·Fluido viscoso Newtoniano e incomprimibile
·Forza peso trascurabile
Voglio determinare la perdita di pressione ( o di
carico) del fluido dovuta a fenomeni di tipo viscoso.Tale perdita di pressione
è infatti causata dalle tensioni
tangenziali che frenano il fluido in movimento,oppure, equivalentemente,se mi
pongo in un punto di vista solidale con il fluido, è dovuta alle tensioni
tangenziali scaricate dal fluido stesso sulle pareti del condotto in modo da
trascinarlo nel suo moto.
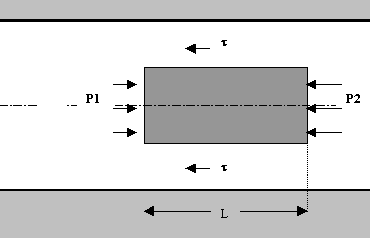
Fig.11:bilancio
delle forze agenti su un elemento di volume di fluido in moto
Il bilancio delle forze, che deve essere nullo, si
compone di 3 contributi: la pressione p![]() che agisce sulla faccia d’entrata, la contropressione p
che agisce sulla faccia d’entrata, la contropressione p![]() sulla faccia d’uscita e la forza tangenziale t che frena il fluido in movimento.
sulla faccia d’uscita e la forza tangenziale t che frena il fluido in movimento.
Considerando positiva la direzione che va da
sinistra verso destra, abbiamo che il contributo di p![]() è positivo, mentre i contributi di p
è positivo, mentre i contributi di p![]() e t sono negativi in quanto vanno in direzione
opposta a p
e t sono negativi in quanto vanno in direzione
opposta a p![]() .
.
L’equazione di bilancio delle forze diventa
quindi:
![]() (14)
(14)
dove 2pRL è l’area laterale del tubo cilindrico e pR![]() è l’area della
sezione del tubo.
è l’area della
sezione del tubo.
Se considero un cilindretto di raggio r < R, la (14) diventa:
![]() (15)
(15)
Sostituisco ora nella (15) la legge di Newton ![]() ed ottengo:
ed ottengo:
(![]() (16)
(16)
ovvero, facendo le opportune semplificazioni,
abbiamo
![]() (17)
(17)
Integriamo ora questa equazione differenziale a
variabili separabili considerando l’ipotesi di aderenza:
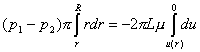 (18)
(18)
cioè,svolgendo i calcoli:
(![]() (19)
(19)
Possiamo ora ottenere la PARABOLA DI POISEUILLE,
cioè la legge che mi descrive come varia la velocità u rispetto al raggio r:
u(r)=![]() (20)
(20)
Possiamo adesso calcolare la velocità media w:
w =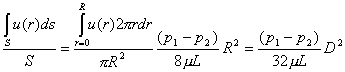 (21)
(21)
Ricavando dalla (21) Dp e moltiplicando e dividendo per wr otteniamo:
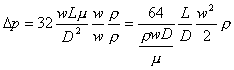 (22)
(22)
Considerando che
![]() arriviamo a dire che:
arriviamo a dire che:
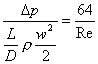 (22)
(22)
Sappiamo
già dalla (14) che 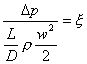 , quindi otteniamo:
, quindi otteniamo:
![]() (23)
(23)
Concludiamo dicendo che l’espressione
![]() (24)
(24)
non ha validità generale in quanto è esatta solo
in presenza delle ipotesi che abbiamo posto all’inizio del paragrafo, ovvero
quando è valida la soluzione parabolica di Poiseuille.
Anche la (23) è valida solo in questo preciso
caso, mentre in tutte le altre situazioni x è diverso e dipende, come abbiamo già detto da 3 parametri: Re, e*, x*.
![]()
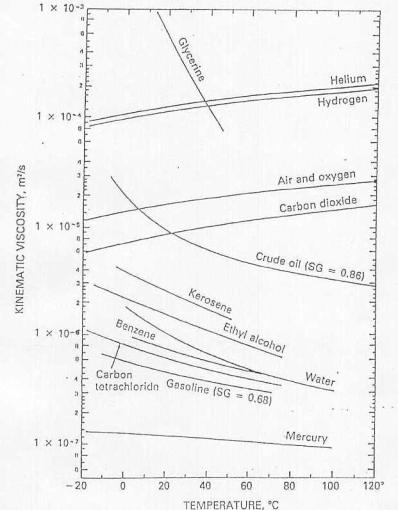
Tabella 1: viscosità dinamica m dei principali liquidi e gas
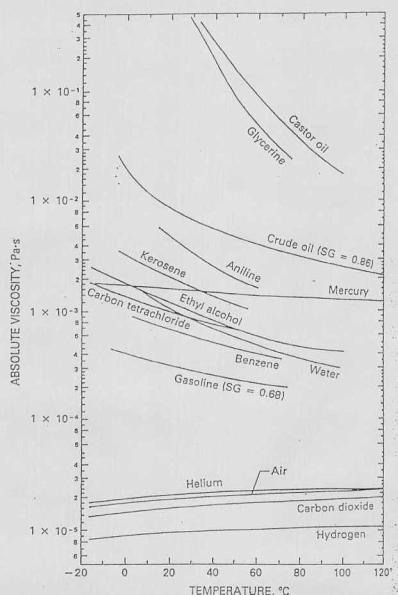
Tabella 2: viscosità cinematica n dei principali liquidi e gas