MISURE
ELETTROACUSTICHE
ED
ISOLAMENTO
ACUSTICO
MISURE ELETTROACUSTICHE
Osserviamo subito che
possiamo fare una distinzione preliminare nello studio della propagazione delle
onde sonore all’interno delle sale:
1.
caratterizzazione
della propagazione dell’impianto elettronico di riproduzione;
2.
caratterizzazione
della propagazione nell’ambiente.
Ovviamente, questi due
aspetti del problema non possono essere scissi nel caso in cui l’obiettivo
delle nostre misurazioni sia quello di ottimizzare l’acustica di una sala, in
cui sia previsto un sistema d’amplificazione. Supponiamo, a scopo
esemplificativo, di dover studiare l’acustica di un’aula progettata per
ospitare uno o più oratori, per esempio docenti che devono tenere una lezione,
e circa duecento ascoltatori, nel nostro caso gli studenti. Evidentemente
poiché l’aula è destinata ad ospitare al suo interno un alto numero di persone
è chiaro che quest’ultima dovrà avere dimensioni elevate, ma quest’esigenza mal
si coniuga con la necessità di garantire ad ogni ascoltatore la sufficiente
chiarezza nell’udire la voce del docente. Possiamo, quindi, pensare di fornire
la nostra aula di un adeguato sistema d’amplificazione, tipicamente composto da
microfoni, amplificatori ed altoparlanti (in sistemi di fascia medio-alta possono
essere presenti anche equalizzatori per migliorare la resa acustica, e sistemi
di ritardo per garantire agli ascoltatori più lontani dall’oratore, che il
suono che viaggia attraverso l’aula giunga comunque prima di quello emesso
dagli altoparlanti). Occorre, però, tenere presente che, essendo i sistemi di
trasduzione elettro-magneto-meccano
acustica assolutamente non lineari, anche il nostro ambiente nel suo complesso,
presenterà delle forti non linearità.
Fatte queste brevi
considerazioni, d’ora in poi trascureremo la presenza di qualsiasi tipo di
impianto elettronico d’amplificazione, limitandoci a considerare esclusivamente
l’ambiente preso in esame.
Ipotesi di campo acustico.
Nel resto della nostra
trattazione assimileremo l’ambiente, oggetto del nostro studio, con un sistema del quale non conosciamo la
struttura interna, ma del quale possiamo misurare l’uscita avendo fornito al sistema un ingresso noto. Cerchiamo ora di dare una migliore veste formale a
questo nostro assunto, e a tale scopo mutuiamo dall’Analisi Matematica il
concetto di funzionale. A questo
punto possiamo quindi affermare che l’ambiente non è altro che un funzionale
che ad un ingresso x(t) fa
corrispondere un ben determinato ed unico segnale d’uscita y(t). La trasformazione del segnale x(t) nel segnale y(t) si
denota nel modo seguente:
![]()
Una rappresentazione
grafica di questa trasformazione è quella in Figura 1. Le frecce indicano i
segnali di ingresso e di uscita, ed il rettangolo rappresenta il nostro ambiente.
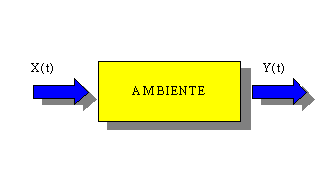
Figura 1
A questo punto
chiediamo che l’ambiente, assimilato ad un sistema, verfichi due importanti
proprietà:
1.
Linearità
2.
Tempo Invarianza
La prima proprietà è
soddisfatta se al sistema è applicabile il principio di sovrapposizione degli effetti. Tale principio
afferma che dati due generici ingressi x1(t)
e x2(t) e note le loro
rispettive uscite y1(t) e y2(t), ottenute applicando
singolarmente gli ingressi, se pensiamo di porre in ingresso una combinazione
lineare di x1(t) e x2(t) l’uscita può essere
ottenuta mediante la stessa combinazione lineare delle due risposte y1(t) e y2(t). Ricorrendo, nuovamente, all’Analisi Matematica
possiamo affermare che un sistema è lineare se soddisfa la relazione:
![]()
dove a e b sono coefficienti costanti. Questa relazione è
chiaramente riportata in Figura 2.
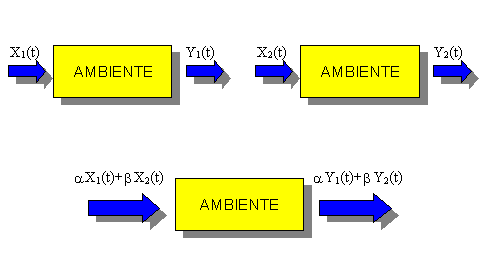
Figura 2
Passiamo ora a
descrivere la proprietà di tempo
invarianza. Definiamo tempo invariante, o equivalentemente stazionario, un
sistema le cui caratteristiche non variano nel tempo. Assumendo che sia:
![]()
il sitema è stazionario
se è soddisfatta la relazione:
![]()
Questa relazione dice,
in pratica, che la risposta corrispondente all’eccitazione traslata nel tempo x(t-t0), ha lo stesso
andamento della risposta al segnale originario x(t), purchè la si trasli della medesima quantità t0.
Una rappresentazione grafica del concetto di stazionarietà è riportata in
Figura 3.
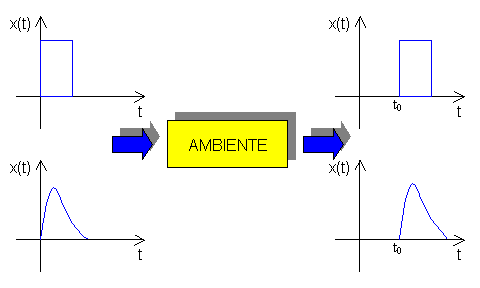
Figura 3
Misura all’impulso.
Nell’ipotesi, quindi,
che il sistema soddisfi entrambe le proprietà di linearità e tempo invarianza,
possiamo misurare la cosiddetta risposta
impulsiva, cioè l’uscita del sistema in corrispondenza dell’eccitazione
impulsiva x(t)=d(t), dove con d(t) indichiamo la funzione
generalizzata impulso unitario, nota anche come delta di Dirac. Questa funzione, tra le varie interpretazioni,
può essere vista come una sorta di elemento
neutro rispetto all’operazione di integrale di convoluzione:
![]()
Convenzionalmente la
risposta impulsiva viene indicata con h(t).
Abbiamo quindi che:
![]()
Da (5) ricaviamo:
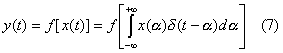
Osserviamo che, avendo
supposto il nostro ambiente lineare, necessariamente il funzionale f[..] deve essere anch’esso lineare.
Quindi, l’operazione di integrale e il funzionale f sono entrambi lineari e quindi è possibile invertirne l’ordine di
calcolo, ricavando:
![]()
Osserviamo che
l’operatore f[..] agisce solo sulle
funzioni dipendenti dal tempo, e lascia quindi invariata la quantità x(a), la (8) allora diventa:
![]()
e infine, per la
proprietà di stazionarietà dell’ambiente e ricordando la definizione di
risposta impulsiva h(t), si ottiene:
![]()
che stabilisce la
seguente relazione fondamentale: il
segnale di uscita può essere
calcolato attraverso la convoluzione
del segnale di ingresso con la risposta impulsiva. Osserviamo che questa
proprietà della risposta impulsiva è valida solo se sono verificate le ipotesi
di tempo invarianza e linearità.
Fino ad ora abbiamo
assunto i segnali di ingresso e di uscita essere segnali a tempo continuo, in realtà, la tendenza moderna è quella
di lavorare su segnali a tempo discreto.
Un segnale a tempo
discreto si può ottenere da un segnale a tempo continuo, mediante l’operazione
di campionamento, che consiste nell’estrarre dal segnale stesso i valori che
esso assume a istanti temporali equispaziati, cioè multipli di un intervallo T
detto periodo di campionamento. Tali valori andranno quindi a
costituire una sequenza il cui valore n-esimo
è il valore assunto dal segnale a tempo continuo all’istante nT. Osserviamo in oltre che tali
valori vengono rappresentati in aritmetica binaria su un numero finito di
cifre(bit), tipicamente 8 o 16.
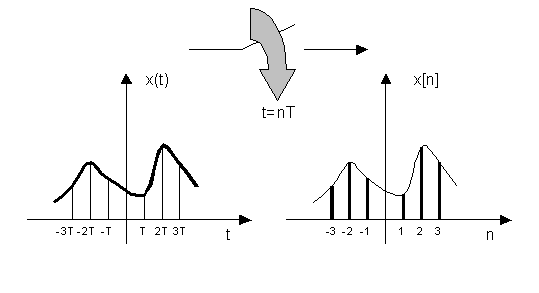
Figura 4
L’operazione di campionamento viene effettuata dai convertitori analogico/digitale,
(comunemente detti convertitori A/D),
mentre l’operazione inversa che ci permette di riottenere un segnale in forma
analogica, cioè a tempo continuo, è assolta dai convertitori digitale/analogico
(D/A). Il motivo per cui oggi si
preferisce lavorare su segnali digitali, cioè a tempo discreto, è la facilità
con la quale si possono elaborare mediante microprocessori specializzati(dedicati),
chiamati DSP (Digital Signal Processor,
elaboratore numerico dei segnali).
Tali microprocessori oltre ad essere estremamente economici, offrono il
grosso vantaggio di poter realizzare diverse funzioni di elaborazione sui
segnali in ingresso, semplicemente cambiando il programma di elaborazione (software),
senza dover minimamente modificare la struttura fisica (hardware) del circuito. Uno schema a blocchi di un tipico circuito
che implementi un DSP è riportato in Figura 5.
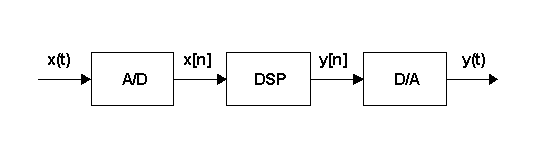
Figura 5
Illustrati questi
ulteriori concetti focalizziamo la nostra attenzione sullo scopo della nostra
trattazione: determinare il funzionale a cui abbiamo assimilato il nostro
ambiente, in maniera tale da caratterizzare completamente ed univocamente
quest’ultimo. Vista la (10), il problema si risolve, univocamente, determinando
la risposta all’impulso h(t). Consideriamo, a tale scopo, un filtro
inverso g(t), tale che la sua convoluzione con x(t) mi dia la
delta di Dirac. Moltiplicando ambo i membri della (10) per g(t)
otteniamo:
![]()
dove si è utilizzata la
proprietà commutativa dell’integrale di convoluzione. Sfruttando la definizione
di g(t), ottengo:
![]()
Ricordando la proprietà
della delta di Dirac di fungere da elemento neutro rispetto alla convoluzione, riscriviamo
la (12):
![]()
A questo punto è lecito
chiedersi se a priori sia semplice determinare g(t) per un qualunque segnale di ingresso x(t).
Come è facile prevedere
la risposta è che in generale è piuttosto laborioso ottenere g(t).
Tuttavia il segnale x(t),
di ingresso, può essere scelto arbitrariamente da noi, quindi nessuno ci vieta
di prendere un x(t) tale che il calcolo del filtro inverso risulti
semplice.
Supponiamo di assumere
come x(t) la delta di Dirac (x(t)=d(t))
e sostituiamo nella (10):
![]()
ottenendo che, preso
come segnale di ingresso la delta di Dirac, il segnale di uscita y(t)
non è altro che la risposta impulsiva da noi cercata.
Ad una tale semplicità
teorica, purtroppo non corrisponde una altrettanto semplice applicazione nella
pratica poiché ci si scontra con la difficoltà nel generare l’impulso unitario
che deve essere brevissimo e di sufficiente potenza (60-80 dB sopra il rumore
di fondo).
Per ovviare a questo
inconveniente si può convolvere il segnale di risposta dell’ambiente con se
stesso rovesciato sull’asse dei tempi, in modo da far diventare primo l’ultimo
campione etc.
Questa tecnica prende il
nome di Time Reversal Mirror, e porta ad avvicinarsi alla d di Dirac
ma non al suo raggiungimento.
Giunti a questo punto si
rende necessaria l’introduzione di un nuovo concetto matematico: la trasformata
di Fourier(FT). Lo scopo è di passare da un analisi nel dominio
del tempo ad una analisi nel dominio della frequenza(nel resto della
trattazione indicheremo in lettera maiuscola i segnali ottenuti attraverso la
trasformata di Fourier dei rispettivi segnali indicati in lettera minuscola).
La ragione principale è
che in ambito frequenziale vale il cosiddetto teorema della convoluzione, che
afferma che convolvere due segnali in ambito temporale è equivalente a fare il
prodotto delle trasformate di Fourier dei due segnali, nel dominio delle
frequenze.
![]()
La (10) ottenuta in
precedenza, applicando la FT, diventa quindi:
![]()
Osserviamo che mentre
nel dominio del tempo sono necessarie m convoluzioni ( a loro volta costituite
da m somme ed m prodotti ) e quindi un numero di operazioni dell’ordine di m![]() , in frequenza ogni armonica viene semplicemente moltiplicata
per un coefficiente per un totale di m operazioni.
, in frequenza ogni armonica viene semplicemente moltiplicata
per un coefficiente per un totale di m operazioni.
Se quindi ripensiamo
alla tendenza moderna ad implementare tali operazioni mediante DSP, ci rendiamo
conto dell’importanza di ridurre il costo di calcolo(inteso come velocità e
quantità di memoria richiesta) delle operazioni che ci sono necessarie. In
quest’ottica, infatti, nascono le note classi di algoritmi efficienti per il
calcolo della trasformata di Fourier che solitamente vengono indicate come FFT(acronimo
di Fast Fourier Transform), tra questi algoritmi ricordiamo
quello noto come algoritmo a decimazione nel tempo.
Se indichiamo con IFFT la trasformata veloce
di Fourier inversa otteniamo:
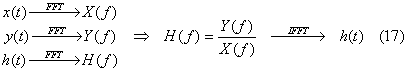
Questa relazione,
afferma che applicando un segnale x(t) al nostro ambiente e misurando il
segnale di uscita y(t), per calcolare la risposta all’impulso è
sufficiente applicare ai segnali x(t) e y(t) la trasformata di
Fourier ottenendo cosi X(f) e Y(f) il cui rapporto ci da H(f),
che usualmente viene chiamata funzione di trasferimento, e che
non è altro che la trasformata di h(t), applicando quindi l’operazione
di trasformata inversa a H(f) otteniamo la nostra risposta all’impulso.
Osserviamo che nel caso
in cui una o più frequenze del segnale in ingresso X(f) abbiano
coefficienti nulli si ottengono dei picchi nella funzione di trasferimento. Per
ovviare a questo problema si mediano i risultati ottenuti su più tentativi nel
tempo (circa cento), e si sceglie x(t) con pari energia su tutte le
frequenze; un segnale siffatto è il rumore bianco che viene chiamato
bianco in virtù del fatto che proprio come la luce bianca “contiene tutti i
colori”, allo stesso modo il rumore bianco contiene componenti a tutte
le frequenze con la stessa intensità.
Per ragioni di ordine
pratico si preferiscono usare in ingresso segnali diversi dal rumore.
Illustriamo due di questi segnali:
1.
Segnali MLS
2.
Segnali Sine Sweep
Segnali MLS
Il segnale MLS
(acronimo di Maximum Length Sequence) è una sequenza binaria del
tipo riportato in Figura 6.
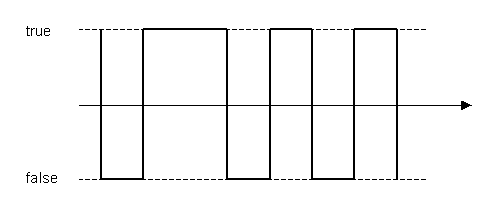
Figura 6
Questo segnale oggi può
essere ottenuto da un qualunque personal computer mediante un software
dedicato, che implementi uno shift register(registro a scorrimento), ma fino a poco tempo fa
venivano utilizzate delle schede che implementavano per via hardware lo shift
register, tra queste schede è famosa quella costruita nel 1989 dall’americano
Douglas Rife, e corredata da un software chiamato MLSSA (melissa)
particolarmente potente, tanto da essere tuttora usato.
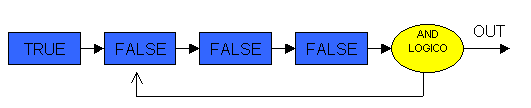
Figura 7
Esempio di shift register a 4 bit
Uno shift register ha
un numero N di celle ed è facile dimostrare che la lunghezza, indicata
con l, ed intesa come numero di bit del segnale MLS generato, dipende da
N secondo la relazione:
![]()
Supponiamo, a scopo
illustrativo, di avere T60@1s e verifichiamo che la (19) sia soddisfatta per
un segnale MLS ottenuto con un registro a 16 celle(N=16). Dalla (18),
otteniamo che la lunghezza l del segnale è pari a: l=216-1=65535.
Se la nostra frequenza di campionamento è, ad esempio, uguale a 44.100Hz,
allora:
L risulta, quindi, essere maggiore del tempo di
riverbero e la scelta del numero di celle si dimostra pertanto sensata.
I vantaggi principali
che ci derivano dall’uso di un segnale MLS sono innanzitutto la semplicità di
calcolo del segnale inverso, essendo noto il segnale a priori, è sufficiente
applicare l’operazione di inversione di Hadamard per ottenere il segnale MLS-1;
la semplicità di calcolo delle operazioni di convoluzione, che essendo il
segnale di tipo binario si semplificano in sole operazioni di addizione.
Inoltre essendo il segnale già in forma digitale risparmio una conversione
analogico-digitale, che pertanto deve
essere fatta solo sul segnale di uscita. Dal momento, poi, che il segnale ha
uno spettro sonoro piatto, come il rumore, ho la possibilità di compiere
un’analisi nel dominio della frequenza, dal momento che la funzione di trasferimento
non presenta quei fastidiosi picchi di cui parlavamo prima.
A fronte di tutti
questi vantaggi c’è però il grosso limite nell’uso di questo segnale, dovuto
alla forte dipendenza dalla linearità del sistema. Infatti, in presenza di
non-linearità si possono avere fenomeni indesiderati come l’attenuazione delle
alte frequenze a causa del loro sfasamento reciproco che le può portare in
controfase, o addirittura alla creazione di echi inesistenti. Si può ovviare in
parte al problema cercando per quanto sia possibile di utilizzare, per la
riproduzione del segnale, altoparlanti estremamente fedeli, ma anche in questo
caso è sufficiente il surriscaldamento dei trasduttori per introdurre nel
sistema forti non-linearità.
Segnali Sine Sweep
Attualmente il segnale
che si preferisce utilizzare è un seno il cui argomento parte dalle frequenze
più basse e giunge fino alle più alte.
![]()
In base al tipo di
relazione che governa la crescita della frequenza si possono distinguere
segnali Sine Sweep di tipo:
1.
Lineare
2.
Logaritmico
Generalmente la
preferenza ricade sui segnali di tipo logaritmico perché questi
hanno il pregio di fornire più energia nella regione delle basse frequenze,
che rappresenta una zona critica, e di procedere più speditamente nella regione
delle alte frequenze. Inoltre lo spettro di un segnale Sine Sweep logaritmico
assomiglia molto a quello di un rumore rosa, ed ha quindi il vantaggio di
essere più gradevole all’ascolto rispetto al rumore bianco.
L’unico inconveniente è
che questo tipo di segnale cade di 6dB per ottava, ma il problema si risolve
facilmente equalizzando il segnale.
Osserviamo, inoltre che
i segnali Sine Sweep hanno una interessante caratteristica: l’inverso di questo
tipo di segnale è lo stesso segnale invertito sull’asse dei tempi, secondo la
tecnica Time Reversal Mirror.
L’unica
controindicazione nell’impiego di questo segnale è la potenza di calcolo che
esso richiede. L’operazione di convoluzione, infatti, non trae nessun vantaggio
dall’utilizzo di questo segnale, e presenta quindi la ben nota complessità di
calcolo. Per questa ragione, infatti, si è incominciato ad utilizzare questo
segnale solo in tempi recenti, ossia da quando gli elaboratori hanno messo a
disposizione maggiore potenza di calcolo.
Va inoltre detto che
passando nel dominio della frequenza per effettuare l’operazione di
convoluzione si può ricorrere all’algoritmo Overlap And Save che
permette di lavorare su un numero di campioni dell’ordine di centinaia di
migliaia.
ISOLAMENTO ACUSCTICO
Negli ultimi le nostre
città sono cresciute nelle dimensioni, ed insieme ad esse è cresciuto il rumore
di sottofondo che ci accompagna nell’arco della giornata. Per questo motivo
solo recentemente è stata riconosciuta la giusta importanza ad un adeguato isolamento
acustico. Nel seguito ci proponiamo, quindi, di illustrare le vie attraverso le
quali si propaga il suono in ambienti tipicamente domestici, con lo scopo di
migliorarne l’isolamento.
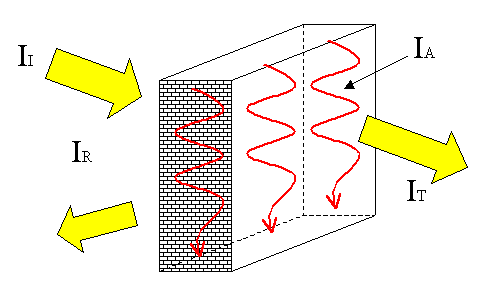
Figura 8
Quando un'onda sonora, IINC
prodotta all'interno di un ambiente incontra una parete la sua intensità sonora
viene in parte riflessa, in parte assorbita dal muro stesso e in parte
trasmessa nell'ambiente adiacente.
![]()
da cui dividendo entrambi
i membri per IINC
otteniamo:
![]()
Chiameremo i tre termini
del primo membro rispettivamente coefficiente di riflessione, coefficiente
d’assorbimento e coefficiente di trasmissione.
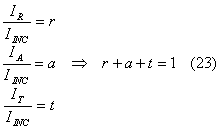
Spesso in acustica si fa riferimento al coefficiente di assorbimento a definito come:
![]()
Questo coefficiente, ci
da una misura della quantità di onda sonora che viene ritrasmessa dopo
l’urto e tiene quindi conto sia della percentuale di onda assorbita, sia della
percentuale che viene ritrasmessa dalla parte opposta. Pensiamo, ad esempio, al
caso di una finestra aperta: questa è un buon assorbente (a grande) perché tutta
l’intensità che riceve viene ritrasmessa verso l’esterno. Quello che noi ci
proponiamo di fare è minimizzare l’intensità dell’onda che viene ritrasmessa,
ossia minimizzare il coefficiente t. Per i nostri scopi quindi la
conoscenza del coefficiente di assorbimento a non è soddisfacente. Proviamo allora a definire
un altro parametro con il quale caratterizzare il potere di isolamento
acustico.
Definiamo il potere fonoisolante R come:
![]()
Dove il segno meno serve
a rendere R positivo, dal momento che il logaritmo è negativo
essendo t<1. Il potere fonoisolante indica, in buona sostanza,
l'abbattimento in dB che il suono subisce passando attraverso una parete. Vale
quindi la relazione:
![]()
Che risulta ancora più chiara in Figura 8.
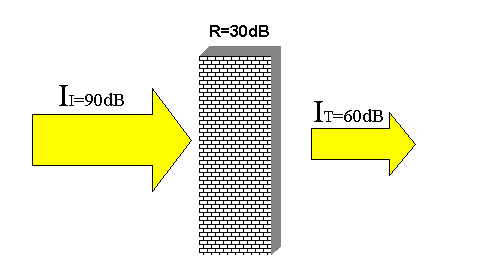
Figura 9
A partire da questa
definizione possiamo pensare di misurare R come differenza di
livello sonoro tra l’ambiente in cui viene generato il suono e quello dove si
ascolta, due stanze adiacenti facenti parte di due appartamenti diversi divise
da una parete cieca (senza porte).
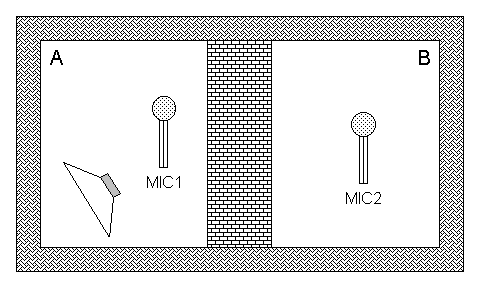
Figura 10
L’altoparlante è rivolto verso un angolo in modo che il suono sia
principalmente riverberato. Le misure
vanno effettuate a tutte le frequenze separatamente (secondo le norme ISO tra 100Hz e 5kHz in bande di 1/3 d’ottava). Se fosse:
![]()
sarebbe molto facile
ottenere R, in realtà il livello LB non dipende solo dal potere fonoisolante ma anche
dalle dimensioni di B, dal suo potere fonoassorbente e dal suo riverbero.
Introduciamo quindi nella (27) un termine correttivo che tenga conto di questi
contributi:
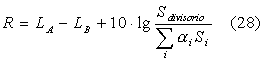
In cui Sdivisorio
è la superficie del tramezzo, ai e Si sono rispettivamente i coefficienti di
assorbimento e le superfici delle altre pareti all’interno dell’ambiente B. A
questo punto misuriamo il T60
di B, ad ogni frequenza:
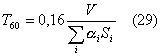
dove V è
il volume della stanza B. Da questa relazione otteniamo poi:
![]()
A questo punto
sostituendo la (30) nella (28) ottengo:
![]()
è lecito chiedersi se non sia possibile stimare il
potere fonoisolante senza effettuare nessuna misurazione di livelli sonori,
sfruttando invece altre proprietà delle materia come la massa. La risposta a
questo quesito è la legge di massa:
![]()
dove s è la densità superficiale della parete in Kg/m2.
Osserviamo che secondo questa legge il potere fonoisolante di una parete non è
costante per tutte le frequenze ma cresce di 6 dB per ottava.
Ad esempio una parete di
cemento, la cui densità sappiamo essere pari a 2400kg/m3, e il cui spessore è uguale a 0,1m avrà
due diversi valori di R alle frequenze di 100Hz e di 1000Hz
dati rispettivamente dalla (33) e dalla (34):
![]()
![]()
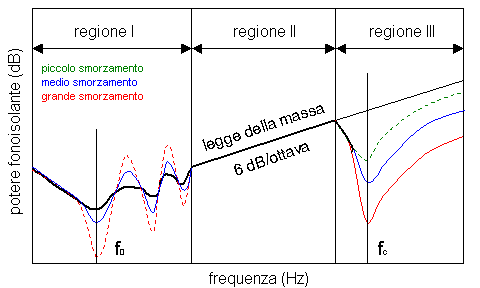
Figura 11
La Figura 11 rappresenta graficamente l’andamento di R in funzione della frequenza.
Nel grafico si possono distinguere tre regioni
principali: è immediato osservare che la legge di massa è rispettata, con le
dovute approssimazioni del caso, solo nella
Regione II, che per i divisori abituali copre un intervallo modesto di
frequenze.
Nella Regione
I si manifesta uno scostamento dalla legge di massa a causa di effetti di
risonanza.
Il divisorio sollecitato
da onde sonore a frequenze coincidenti con quelle proprie di vibrazione entra
in risonanza e conseguentemente il suo potere fonoisolante tende a diminuire
per raggiungere un minimo alla frequenza fondamentale fo, che è la più bassa delle frequenze
naturali.
Il fenomeno è più o meno
evidente in funzione dello smorzamento interno, il cui effetto si traduce in un
più o meno rapido annullarsi delle vibrazioni, generatesi nella struttura, per
effetto di una qualunque sollecitazione esterna; ciò da ragione delle curve a
tratto discontinuo, valide per smorzamento grande, medio e piccolo.
Si noterà come al
crescere dello smorzamento interno i picchi di risonanza tendano ad
appiattirsi.
Fortunatamente il
fenomeno ha scarsa importanza pratica ai fini dell’attenuazione del suono,
almeno nel caso di pareti (o pavimenti) normalmente impiegati nell’edilizia,
dato che per essi la frequenza naturale fondamentale fo
si colloca intorno ai valori di 10-20 Hz, e comunque quasi sempre inferiori a
100 Hz.
Nella Regione III la
legge della massa non è più valida a causa del fenomeno della conincidenza.
Sappiamo che in ogni istante ci sono punti della parete su cui l'onda acustica
esercita il massimo della pressione sonora, altri dove il carico è nullo e
altri ancora dove è negativo; come conseguenza la parete tende a flettersi con
una certa lunghezza d'onda lF che dipende dall'angolo q, e dalla
lunghezza d’onda del suono incidente. Ogni parete, inoltre, ha una propria
lunghezza d’onda lNAT,
che si può determinare facendo vibrare la parete con uno strumento apposito
chiamato shaker. Il fenomeno della coincidenza si ha quando la lunghezza
dell'onda del campo è uguale alla lunghezza d'onda naturale, misurata per un
carico alla stessa frequenza, in questo caso si ha un più efficace
trasferimento di energia sonora dall’aria alla parete e, quindi, una
diminuzione del potere fonoisolante di quest’ultima.
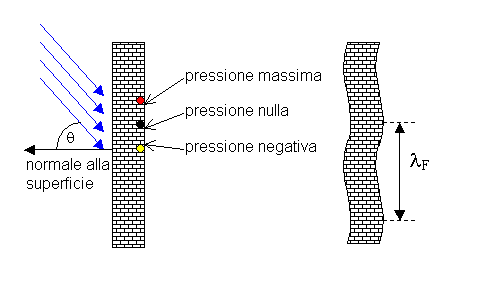
Figura 12
La frequenza alla quale si ha il fenomeno della coincidenza
si può calcolare mediante la relazione:
![]()
valida per i materiali impiegati nell’edilizia,
dove:
E = modulo di elasticità
s = coefficiente di Poisson
r = densità del materiale
s = spessore del materiale
c0 = velocità di propagazione del suono
nell’aria ( @
343 m/s).
Va detto, inoltre che l’ampiezza
del fenomeno dipende dal fattore di smorzamento del materiale: per materiali
"canterini" come il vetro, con fattore di smorzamento basso, R ha una grande caduta. Per questo
motivo si usa un vetro camera, fatto da due lastre di diverso spessore (quindi
con diversa frequenza di coincidenza) separate da uno strato d'aria o ancor
meglio da un film plastico antisfondamento come quello usato per le vetrate
delle banche che fa da cuscinetto elastico smorzante. Inoltre, si può osservare
che più la parete è sottile più aumenta la frequenza di coincidenza.
In chiusura osserviamo
che fino ad ora abbiamo del tutto trascurato la presenza nei muri di
imperfezioni quali micro fessure e cammini di fiancheggiamento come ad esempio
condotti di aerazione, tubi di vario genere, guide metalliche dell’ascensore,
ecc., che sicuramente influiscono negativamente su R.