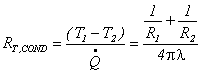Richiami sulla resistenza termica equivalente
Ai fini della progettazione di impianti di riscaldamento o sistemi di raffreddamento si può evitare di risolvere l’equazione differenziale di Fourier per ogni situazione trasferendo il problema nell’ambito delle ben note reti elettriche: le pareti, i condotti ed ogni altra superficie o fonte di dispersione si rappresenta mediante una resistenza termica equivalente sostituendo ai potenziali le temperature ed alle correnti i flussi termici.
Per definizione di resistenza termica è:
![]()
formalmente analoga alla legge di Ohm.
Ricordiamo alcuni risultati ottenuti dall’integrazione della legge di Fourier per geometrie piane e cilindriche utili in seguito:
q lastra a facce piane e parallele di spessore d, superficie S, e coefficiente di conduzione l:
![]()
q condotto cilindrico di raggio interno R1, raggio esterno R2, lunghezza L, conduzione l:
Esaminiamo ora la terza tipica geometria che, insieme alle precedenti,
permette di risolvere agevolmente gran parte dei problemi avvalendosi
dell’analogia elettrica.
Sfera cava
Consideriamo un sistema costituito da una sfera cava di raggio interno R1 e raggio esterno R2 costituita da materiale con conducibilità termica l le cui superfici si trovino rispettivamente alle temperature T1 e T2.
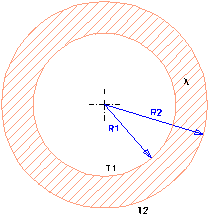
La potenza complessiva scambiata è indipendente dal raggio ed è pari al prodotto del flusso termico per la superficie in esame:
![]()
La legge di Fourier si scrive come:
![]()
che conduce all’equazione differenziale del primo ordine a variabili separabili:
![]()
Integrando il primo membro tra R1 e R2 ed il secondo tra T1 e T2:
![]()
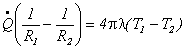
si ottiene l’espressione dell’energia emessa per unità di tempo dalla sfera:
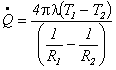
che, ovviamente, è indipendente dalla superficie sulla quale viene misurata.
A questo punto è immediato calcolare il valore di resistenza termica equivalente della sfera cava che vale:
Cenni sullo scambio termico per convezione
Nel caso di moti convettivi la dipendenza funzionale del flusso termico q (energia trasmessa per unità di tempo per unità di superficie) dal gradiente di temperatura non è di tipo lineare, come previsto dalla legge di Fourier, tuttavia è possibile ,ed estremamente utile, ricondursi ad una forma semplice introducendo un fattore di proporzionalità tra q e DT :
![]()
dove h, di dimensioni W/m2K, è chiamato coefficiente di convezione nonostante tale nome debba essere riservato, secondo il Sistema Internazionale, unicamente a termini adimensionali.
Analogamente possiamo definire la potenza complessiva scambiata per convezione:
![]()
dove S indica la superficie in esame.
Il coefficiente di convezione, funzione di diverse grandezze tra cui la temperatura del materiale stesso, può essere determinato mediante la teoria dei modelli e le formule di calcolo sono tabulate per diverse situazioni.
Ai fini della risoluzione di problemi di scambio termico, il contributo convettivo può essere vantaggiosamente rappresentato da una resistenza equivalente di valore:
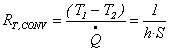
Esercizio
1
Si determini la potenza necessaria per mantenere un locale a 20°C quando la temperatura esterna è 0°C ed il muro divisorio, costituito in mattoni dello spessore di 20cm, ha una superficie di 15m2.
S=15m2
T1=20°C
T2=0°C
h1=8W/m2K
h2=20W/m2K
l=1W/m·K
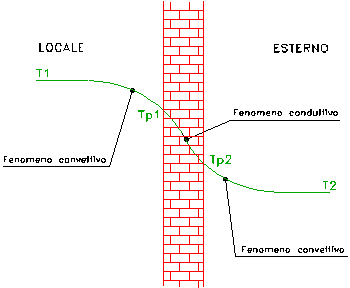
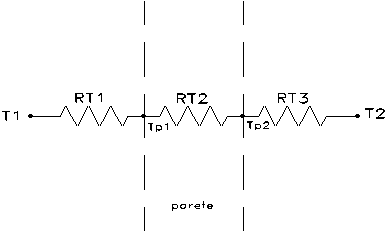
In prossimità della parete l’aria è soggetta a moti convettivi che ne abbassano la temperatura cosicché la rete elettrica equivalente è costituita complessivamente da tre resistenze connesse in serie, poiché il flusso di calore inizialmente attraversa lo strato d’aria interno, quindi la parete ed infine lo strato esterno.
![]()
![]()
![]()
La resistenza equivalente della serie è:
![]()
da cui si ottiene l’energia dispersa dalla parete per unità di tempo che coincide con la potenza necessaria per mantenere costante la temperatura nella stanza:
![]()
valore da confrontare con i 1500W richiesti, nella stessa situazione, trascurando gli effetti convettivi dell’aria a contatto con la parete.
Cenni sullo scambio termico per irraggiamento
Sulla falsa riga del ragionamento compiuto per affrontare i problemi di scambio convettivo, è conveniente introdurre un fattore di proporzionalità tra flusso termico e differenza di temperatura che semplifichi la relazione, considerevolmente non lineare, tra queste grandezze; l’espressione che le lega si traduce allora nella semplice equazione:
![]()
e, al solito:
![]()
Il coefficiente di irraggiamento hR (ancora una volta la nomenclatura del Sistema Internazionale e quella corrente sono in disaccordo!) si misura in W/m2K ed è sensibilmente variabile.
Molte volte è irrilevante determinare i singoli contributi convettivi e radianti perciò essi vengono valutati congiuntamente mediante il coefficiente di adduzione a definito come la somma di h e hR.
Infatti la somma delle equazioni:
![]()
![]()
è:
![]()
La legislazione italiana (legge 10/91) prevede, per la progettazione di impianti di riscaldamento e di termoisolamento, l’utilizzo dei coefficienti a tabulati dalle norme UNI che stabiliscono anche le temperature ambientali di riferimento nelle diverse zone del paese.
Naturalmente l’utilizzo di queste formule conduce a risultati tanto più precisi quanto più è piccola la differenza tra le temperature considerate, cosicché l’arco di curva q(DT) possa essere approssimato al meglio.
Esercizio
2
Si determini la potenza necessaria per compensare la dispersione di un serbatoio contenente acqua alla temperatura di 100°C se all’esterno vi sono 0°C. La parete del contenitore è composta da una lastra in ferro, di spessore 5cm, rivestita da un’alterna serie di pannelli, spessore 10cm, in cemento dalle caratteristiche differenti.
TA=100°C
TB=0°C
hA=200W/m2K
hB=10W/m2K
lA=60W/m·K (lastra in ferro)
lB1=1W/m·K (pannello in cemento 1)
lB2=0.1W/m·K (pannello in cemento 2)
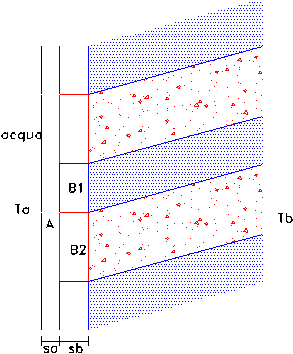
Consideriamo una porzione elementare di sezione complessiva 3 m2:
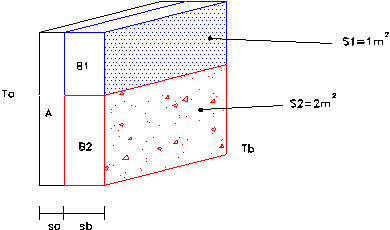
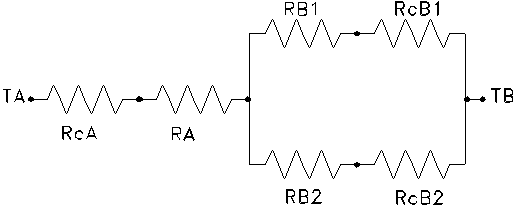
La rete elettrica equivalente, nella quale le temperature di parete TpB1 e TpB2 sono giustamente considerate diverse, è la seguente:
Ai fini di semplificare i calcoli successivi è possibile tracciare un secondo schema che, tuttavia, risulta meno aderente alla realtà; il trucco consiste nel considerare la lastra di ferro ripartita in due elementi, distinti e congiunti, la cui sezione è pari a quella dei pannelli in cemento a contatto:
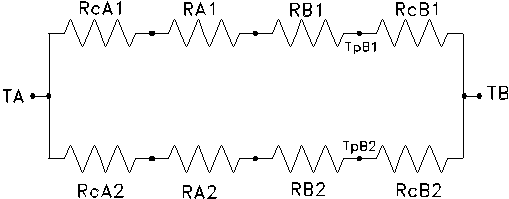
resistenza di convezione acqua: ![]()
resistenza di conduzione ferro A1: ![]()
resistenza di conduzione cemento B1: ![]()
resistenza di convezione aria: ![]()
La resistenza totale del primo ramo è la somma dei singoli contributi:
![]()
resistenza di convezione acqua : 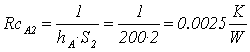
resistenza di conduzione ferro A2: ![]()
resistenza di conduzione cemento B2. 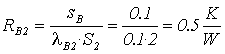
resistenza di convezione aria: 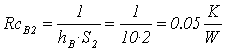
![]()
Note le temperature TA e TB è possibile calcolare le potenze termiche dissipate dai due rami:
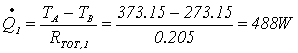
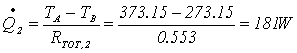
La potenza richiesta per far fronte alla dissipazione da parte della parete del serbatoio è:
![]()
Calcoliamo, infine, le temperature di parete dei blocchi in cemento:
![]()
![]()
In realtà la variazione di temperatura non è netta infatti, in corrispondenza dei giunti strutturali B1/B2, si ha passaggio di calore che aumenta inevitabilmente la potenza dispersa; per calcoli simili è quindi consigliabile adottare un coefficiente di sicurezza che consideri questi fenomeni secondari.
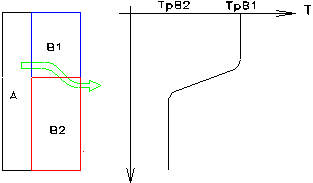
Conduttori
elettrici isolati
E’ noto che qualsiasi corpo percorso da corrente è soggetto al fenomeno del riscaldamento per effetto Joule che può condurre, in circostanze estreme, alla fusione del materiale; nel caso dei conduttori elettrici che, per ovvi motivi, necessitano di una guaina isolante, il raffreddamento sembra ostacolato dal rivestimento stesso. Un’analisi più approfondita mostra come l’isolante, non solo non peggiora la situazione, ma, al contrario, migliora la capacità di raffreddamento: infatti l’aumento della superficie di scambio con l’aria prevale, almeno inizialmente, sull’effetto di resistenza termica dell’involucro (tipicamente PVC o gomma sintetica).
Consideriamo allora un conduttore di lunghezza L, raggio R1 con rivestimento protettivo di raggio r, coefficiente di conduzione l e soggetto a convezione parametrizzata da h:
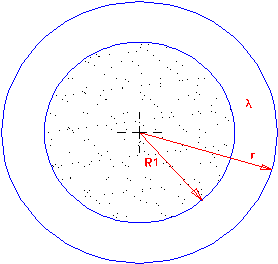
La resistenza termica dell’isolante comprende i contributi di conduzione e di convezione:
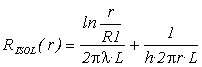
Derivando rispetto al raggio esterno ed uguagliando a zero si ottiene il raggio critico (rC), tale cioè da minimizzare la resistenza termica:
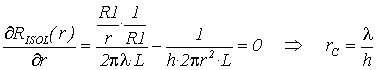
che, evidentemente, è funzione della situazione in cui il cavo si trova: è per questo motivo che i conduttori si differenziano a seconda della posa cui sono destinati (interrati, sottotraccia, in canalina,ecc...).