Alessi Roberta – Lezione del 31/10/2000 ore
14.30-16.30
Perdite di Carico
Le perdite di carico sono il rapporto fra le perdite di pressione e la densità di un fluido che si verificano lungo un qualsiasi impianto idraulico. Esse si possono classificare in:
· Perdite di carico distribuite lungo tutto il condotto dovute a scabrezza della condotta e a viscosità del fluido.
· Perdite di carico localizzate causate da irregolarità geometriche poste lungo il condotto.
Perdite
di carico distribuite
Consideriamo la velocità media di un fluido lungo un condotto cilindrico a sezione costante:
![]()
dove con p1 e p2 indichiamo le pressioni in corrispondenza della sezioni specifiche, con Re il numero di Reynolds, con m la viscosità dinamica e con L la lunghezza del condotto.
Ricaviamo da essa la variazione di pressione:
![]() .
.
Determiniamo ora l’espressione delle perdite di carico in funzione del numero di Reynolds. Questo determina la differenza fra moto laminare e turbolento:
![]()
dove con D si indica il diametro della sezione del condotto.
Nel caso di regime laminare in condotta liscia a sezione circolare costante :
![]()
![]()
![]()
dove ![]() in questo caso
identifica il fattore di attrito che chiameremo x .
in questo caso
identifica il fattore di attrito che chiameremo x .
Otteniamo così un’espressione più generale delle perdite di carico distribuite:
![]()
Nel caso di regime turbolento la
relazione di ξ è più complessa e dipende oltre che da Re anche dalla
scabrezza relativa del condotto ![]() .
.
![]() .
.
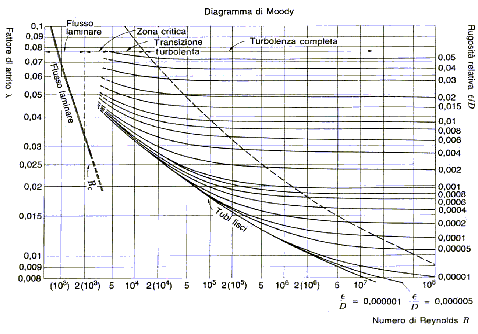
Il comportamento del fattore di attrito si studia grazie al diagramma di Moody qui rappresentato.
Questo si divide essenzialmente in 3 zone. La prima, sulla sinistra rappresenta l’andamento del fattore di attrito per un fluido in regime laminare.
La seconda parte, al centro, è la zona di transizione nella quale il fluido assume un comportamento intermedio. A destra del grafico,invece, abbiamo la zona per un fluido in regime turbolento.
Ciascuna curva presente in questa zona si riferisce ad una diversa scabrezza relativa.
In realtà anche questo diagramma
è una semplificazione, perché non considera la dipendenza (considerata
trascurabile) del fattore di attrito dalla distanza relativa dall’ingresso del
fluido nel tubo ![]() .
.
Perdite
di carico concentrate
Le perdite di carico concentrate sono dovute ad irregolarità geometriche (variazioni di pressione, raccordi, ecc) oppure a ostacoli (valvole, misuratori, filtri) presenti nel condotto dove scorre il fluido.
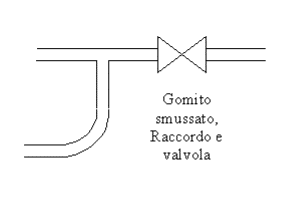
Per esprimere matematicamente le perdite concentrate utilizziamo la seguente espressione:
![]()
dove b è il coefficiente di perdita concentrata che varia a seconda della discontinuità particolare che stiamo considerando, r la densità del fluido.
Qui di seguito mostriamo la tabella relativa al coefficiente b per vari tipi di discontinuità.
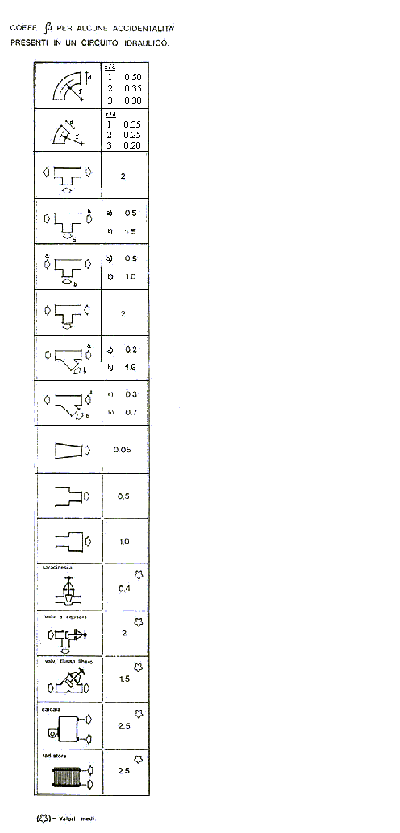
Possiamo notare che le perdite di carico concentrate, come ci aspettavamo, non dipendono dalla lunghezza del condotto nel quale scorre il nostro fluido.
Inoltre dall’espressione della portata massica:
![]()
![]()
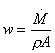 (con A area della
sezione del condotto)
(con A area della
sezione del condotto)
si deduce che le perdite di carico concentrate dipendono dal quadrato della portata massica.
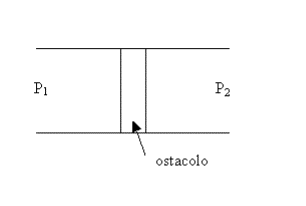
Vediamo ora come varia la velocità del fluido in corrispondenza di un ostacolo,per esempio una strozzatura, che causa una variazione di pressione:
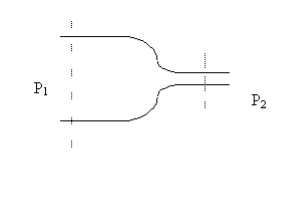
Nei 2 punti considerati la portata massica deve essere la stessa:
![]() r1A1w1
= r2A2w2
r1A1w1
= r2A2w2 ![]()
con D diametro della sezione circolare del condotto.
Quindi, riassumendo, quando si progetta un sistema idraulico bisogna tenere conto di entrambi i tipi di perdite: distribuite e concentrate.
Il primo termine del secondo membro dell’equazione è la sommatoria delle perdite di carico distribuite nei tratti in cui il condotto è rettilineo, mentre il secondo è la sommatoria delle perdite di carico concentrate dovuta alle discontinuità presenti nel sistema.
Diametro equivalente
Finora abbiamo sempre considerato condotti a sezione circolare. Per poter studiare il moto dei fluidi in condotti di sezione qualsiasi dobbiamo introdurre il concetto di diametro equivalente, così da poter utilizzare per le perdite distribuite, in condotti di qualsiasi sezione, la stessa formula che abbiamo prima illustrato.
Definiamo come diametro equivalente il rapporto:
![]()
dove con A abbiamo indicato l’area della sezione del condotto e come Perimetro bagnato il perimetro che il liquido tocca all’interno del condotto.
Consideriamo per esempio un condotto a sezione circolare di diametro D:
![]()
![]()
Per le altre sezioni varia inoltre la formula del fattore di attrito, come vediamo qui di seguito:

Valutato
il valore del diametro equivalente per il nostro condotto, si calcolano tutte
le perdite di carico distribuite e concentrate per potere dimensionare la pompa
che mantiene il liquido nel sistema idraulico alla pressione desiderata.
Lunghezza
equivalente
Per
le perdite concentrate possiamo introdurre il concetto di lunghezza
equivalente. In sostanza si rapporta la perdita di carico concentrata ad una
perdita di carico distribuita su una determinata lunghezza di condotto.
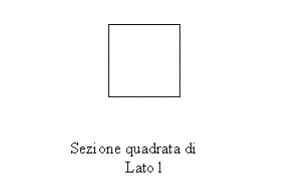
La
lunghezza equivalente riferita a tali perdite concentrate si ricava tramite il
diagramma riportato successivamente, in cui il primo asse sulla sinistra si
riferisce al tipo di perdita concentrata che stiamo considerando. L’asse a
destra al diametro interno del condotto espresso in mm ed infine l’asse nel
mezzo si riferisce alla lunghezza equivalente cercata in m.
Per
esempio, consideriamo un raccordo a squadra 90°, con diametro interno del
condotto di 50mm: la lunghezza equivalente per questa perdita di carico
concentrata è di 4m. (linea blu sul grafico).
In
questo modo, utilizzando la lunghezza equivalente, è possibile eliminare la
dipendenza della perdita di carico totale dalle perdite di carico concentrate.
Esercizio:
Utilizzo del diagramma di Moody per perdite di carico distribuite
Calcolare
le perdite di carico che si hanno in un condotto di lunghezza L a sezione
circolare, diametro D costante, contenente ammoniaca.
I
dati del problema sono:
D=50.8mm
(diametro condotto)
L=22.86m
(lunghezza condotto)
T=-12.2°C
(temperatura fluido)
W=21.3m/s
(velocità fluido)
e=0.046 10-3m (asperità media
condotto)
m=8.6 10-6Pa.s (viscosità dinamica)
r=2.1Kg/m3 (densità ammoniaca)
Per
determinare le perdite di carico, mi occorre conoscere il fattore di attrito x, esso può essere ricavato dal diagramma
di Moody.
Dobbiamo
per prima cosa capire in che regime di moto si muove il fluido all’interno del
condotto, quindi calcolo il numero di Reynolds:
![]()
Ci
troviamo quindi in regime turbolento e nella 3° zona del diagramma di Moody.
Per
potere trovare il fattore di attrito sul diagramma, mi occorre anche la
scabrezza relativa del condotto:
![]()
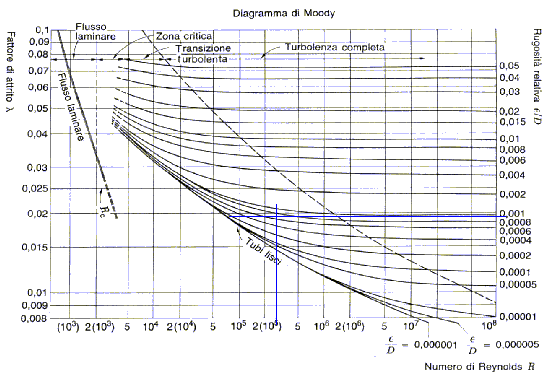
Otteniamo quindi un fattore di attrito pari a circa :
x=0.002
e quindi ora possiamo ricavare le perdite di carico relative alla sezione di condotto considerata:
![]() .
.
Dall’equazione di Navier
all’equazione di Bernoulli
Al posto dell’equazione di Navier, per impieghi comuni, viene utilizzata una versione semplificata: l’equazione di Bernoulli.
Consideriamo un tubo di flusso all’interno di un condotto:
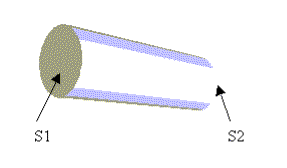
Supponiamo che il fluido si trovi in regime stazionario e integriamo l’equazione di Navier sul tubo di flusso considerato:
![]()
dove con a si intende il coefficiente di profilo di velocità (varia a seconda del condotto all’interno del quale consideriamo il tubo di flusso e solitamente si considera pari a 1), con w le velocità medie del fluido che attraversa la superficie relativa, con z si intende il centro geometrico delle superfici che delimitano il tubo di flusso, g è l’accelerazione gravitazionale, v il volume specifico del fluido, p la pressione, T la temperatura assoluta, S la superficie che delimita il tubo, l il lavoro specifico.
L’ultimo integrale rappresenta l’energia meccanica specifica dissipata, più il fluido è viscoso più tale quantità è maggiore e si parla quindi di resistenza idraulica, facendo un’analogia con i circuiti elettrici.
Quella che abbiamo trovato è l’equazione di Bernoulli. Possiamo immediatamente notare che ci sono forti analogie con il 1°Principio della Termodinamica per i sistemi aperti:
![]()
dove con h intendiamo l’entalpia specifica e con q il calore specifico del fluido considerato.
Possiamo notare che, affinché le due equazioni considerate coincidano, deve essere:
![]()
poiché
![]()
integrando si ottiene:
![]()
dove con qsc si intende il calore specifico scambiato dal fluido con l’ambiente e con qdiss il calore specifico dissipato dal fluido (resistenza idraulica).
Abbiamo quindi ottenuto che le due equazioni coincidono.
L’equazione di Bernoulli è largamente utilizzata in forma semplificata: consideriamo infatti il fluido nel condotto con densità costante r=cost, quindi:
![]() (volume
specifico costante)
(volume
specifico costante)
![]()
Quindi otteniamo l’equazione di Bernoulli in forma semplificata:
![]()
dove con R si intendono le perdite di carico che abbiamo trattato nel precedente capitolo:
![]() .
.