Cross Talk Cancellation - Theory and Practice

When You listen through loudspeakers at signals convolved with Binaural Impulse Responses (BIRs), or directly recorded with a dummy head, You cannot avoid the Cross-talk effect: the signal emitted from the left loudspeaker reaches also the right ear, and vice-versa.

Anyway, You can design special cross-talk canceling filters, which must be applied to the original BIRs prior of the convolution with the anechoic signal(s)., or directly to the binaural recording.

Schematic of the convolution/auralisation process:

The figure above shows what happens when a couple of loudspeakers is placed in front of the listener's head: the signal coming from each loudspeaker reaches both the ears, and so at the ear channel entrance both Left and Right channels arrive mixed.

Furthermore, the Head Related Transfer Function is already inserted in the IRs used for convolution, but the signals coming from loudspeakers newly interfere with the listener's head, so the head filtering is applied twice! For these reasons, a more involved processing is needed. In mathematical notation, the signals arriving at the Left and Right ear channel entrance of the listener's head can be described as:

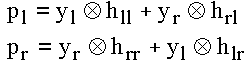
in which the stereo signal yl and yr were derived from a single mono input x, through convolution with the two binaural IRs hl and hr. Passing to the frequency domain by FFT, the previous relations can be rewritten as:

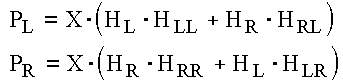
Now, let we substitute two adequate IRs (hl' and hr') instead of the original ones: they must be capable to make the terms in parenthesis equal to the (wanted) BIRs HL and HR. After a few passages, we get:

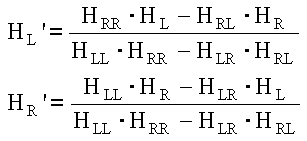
In principle, at this point a simple IFFT would make it possible to obtain the new IRs hl' and hr', which include the cross-talk cancelling effect and the original BIRs. This is not true, as this simple inversion process produces unstable, acausal FIR filters. We need again to use the Kirkeby theory to obtain least-squares inverse FIR filters, making use of the Invert Kirkeby module.

You need to perform these steps:

1. Measuring the reproduction HRTF impulse responses (H, 4 IRs)
2. Compute their inverse set (F, also 4 IRs)
3. Convolve them with the original stereo IRs (G) or directly with the binaural recording

Through the above process, not only the crosstalk is eliminated, but also any unwanted frequency filtering due to loudspeaker response is equalized. Furthermore, the head-related transfer function is eliminated too, avoiding the double-filtering due to the superposition of the listener's head with the head already included in the original BIR. In theory this processing could also eliminate reflections on the listening room's walls, and this way a special listening environment should not be necessary. But this is quite difficult to obtain, as the dereverberation is a very unstable process, and it works only for the exact position of the listener's ears in which the loudspeaker measurements were made.

For maximum automatisation of the whole process, a CoolEdit Macro can be created, which performs all these tasks without the need of human intervention.